一种多功能并网逆变器拓扑及其控制
2013-10-23赵荣祥朱明磊汤胜清
曾 正,杨 欢,赵荣祥,汤 浩,朱明磊,金 磊,汤胜清
(浙江大学 电气工程学院,浙江 杭州 310027)
0 引言
为了更好地实现分布式可再生能源并网,集成了可再生能源、局部负荷和储能的微电网技术作为一种局部供电系统引起了广泛的关注[1-5]。并网逆变器作为分布式发电系统和微电网技术中的关键部件之一,近年来得到了深入的研究[6-8]。
分布式发电系统和微电网内的不平衡、无功和谐波电流严重影响了公共耦合点PCC(Point of Common Coupling)处的电能质量,甚至会给并网逆变器的控制带来不利影响[9]。若要治理PCC处的电能质量,最常用的方法是安装有源或无源滤波器,但这需要额外的装置,增加了系统的体积和成本。为了提升并网逆变器的运行性能,提高其性价比,有学者提出了具有复合功能的多功能并网逆变器MGI(Multifunctional Grid-connected Inverter)[10]。 文献[11-12]给出了单相并网逆变器复合有源滤波功能的MGI拓扑。文献[13-14]进一步提出了复合有源滤波功能的三相全桥MGI拓扑。由于三相桥式拓扑带不平衡负载的能力不强,为了更好地实现对不平衡负载的补偿,文献[15]提出了一种三相四桥臂的MGI拓扑。为了使并网逆变器能同时治理电流和电压电能质量问题,文献[16-17]提出了能同时补偿谐波电流和电压跌落的MGI拓扑。但现有MGI拓扑对直流电压的要求比较高,往往需要多组直流模块(光伏电池、储能单元)串联或通过前级DC/DC变换升压才能接到其直流端。此外,就电流补偿而言,能同时补偿谐波、不平衡和无功电流的MGI拓扑还不多见。
本文针对一种能同时补偿无功、不平衡和谐波电流的MGI拓扑进行了研究,该拓扑由3组单相全桥逆变器构成。由于采用了升压隔离变压器,故能明显降低对直流侧的要求。同时,隔离变压器还能极大降低逆变器输出直流及谐波分量对电网的影响[18]。本文建立了该拓扑的详细数学模型,设计了其控制器,并给出了指令电流的生成算法。最后,仿真和实验结果验证了所提方法的正确性和有效性。
1 MGI拓扑及其控制
1.1 MGI的拓扑及数学模型
本文研究的MGI拓扑如图1所示,该拓扑由3组独立的单相全桥逆变器共用一组直流母线构成。考虑到光伏电池、储能单元的输出电压一般比较低,直流母线电压不宜设计过高,这里直流母线电压Udc取为400 V。3组单相全桥逆变器分别构成a、b、c三相,经LC滤波器接入隔离变压器,隔离变压器的输出端连接到PCC,该处接有非线性负荷、三相不平衡负荷,并与三相四线制配电系统相连。
从图1可以看出,3个单相全桥逆变器相互解耦,可以看作3个独立的单相逆变器。在建立逆变器的数学模型时,可忽略负载的影响,并取任意一相进行分析,其电路如图2所示。其中,L1和L2分别为隔离变压器的原边和副边漏感;Lm为激磁电感;Ls为系统电感;L、C和R分别为滤波电感、滤波电容以及阻尼电阻;uo和us分别为单相逆变器的输出电压和PCC处的电压;ups和ips分别为隔离变压器的副边电压和电流折算到低压侧的值;隔离变压器的原副边变比为 N1∶N2;iL、it和 io分别为逆变器滤波电感、隔离变压器原边和副边电流。
从图2中的阻抗网络部分可以看出,隔离变压器的原边电感L1、激磁电感Lm和滤波电容支路共同构成了一个△环,利用电路理论中的△-Y变换[19],可以得到如图3所示的等效阻抗网络。

图1 一种MGI拓扑Fig.1 A kind of MGI topology

图2 MGI单相拓扑等效电路Fig.2 Single-phase equivalent circuit of MGI

图3 阻抗网络的变换结果Fig.3 Result of impedance network transform
值得指出的是,由于阻尼电阻较小,可忽略不计。在图3中,阻抗Z1、Z2和Z3可分别写为:

由图3,应用电路理论中的叠加原理,可得其电压uo到电流ips、iL之间的传递函数为:

文献[20]提出了一种基于加权电流反馈的控制方法,并利用该方法将三阶LCL滤波并网逆变器模型降阶为一阶模型,以方便控制器的设计。这里进一步利用该思想来实现图2所示MGI模型的降阶。定义加权电流i作为等效的反馈量:

那么,系统对输入电压uo到电流i之间的传递函数为:
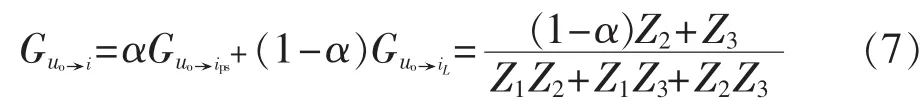

由于变压器的激磁电感远大于原副边的漏感,即L1≈L2=Lm,故:
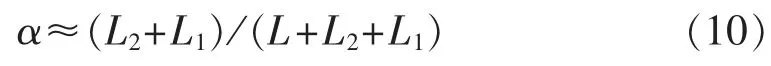
那么式(8)可简化为:

可见,降阶后的模型式(11)是一个一阶系统,且只由系统中的电感参数决定。可以方便地利用式(11)所示降阶模型设计MGI的控制器。
1.2 PI控制参数的整定
由前面的分析,可以得到MGI在PI控制器下的框图模型,如图4(a)所示。其中,KPWM为逆变器的放大系数,对于双极性调制的单相全桥逆变器,KPWM=Udc。图4(b)给出了基于降阶模型的控制器设计框图。

图4 MGI框图Fig.4 Block diagram of MGI
针对式(11)所示开环传递函数模型,设计PI控制器的参数。首先考虑比例环节的系数Kp,系统在比例环节作用下的开环传递函数为:
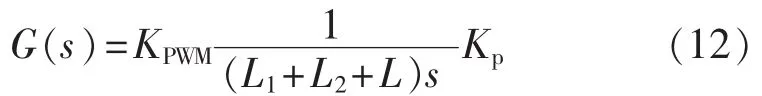
以保证系统的闭环系统穿越频率小于开关频率fs=10 kHz为依据来设计Kp,以保证开环系统在开关频率附近的增益低于0 dB,据此可得:

系统参数如下:L=1 mH,C=10 μF,R=4 Ω,L1=L2=0.5 mH,Lm=0.6 H,Udc=400 V,N1∶N2=150∶220。由式(13)有:

由于Kp越大系统静态误差越小,取Kp=0.3。
在比例环节的基础上引入积分环节后,系统的开环传递函数为:

为保证PI的转折频率不影响原系统的穿越频率fc,需要满足的条件为PI补偿环节的转折频率远小于系统穿越频率,这里取为穿越频率的1/50,即:

计算可得:

由于Ki越大系统动态性能越好,取Ki=350。
基于以上设计的PI控制器,可得闭环系统的Bode图如图5所示。可见,受控系统在低频段具有0 dB的增益和0°的相移,能较好地保证对指令电流信号的跟踪。而对于高频段具有较大的衰减速率,从而保证对高次谐波的抑制能力。
1.3 滤波器中阻尼电阻的设计
由图2所示阻抗网络和式(8)易知该系统存在一个谐振回路。该回路易引起谐振频率附近的谐波电流谐振,导致系统不稳定或静差过大。本文采用滤波电容支路串联电阻的方法来对谐振加以阻尼与抑制,如图6所示。
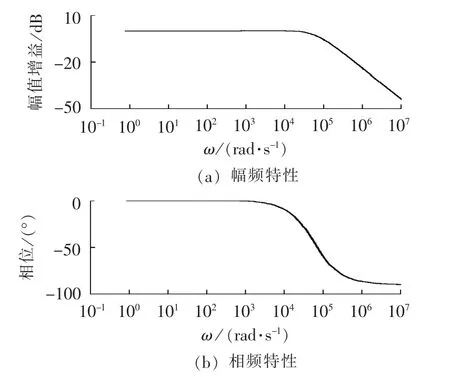
图5 降阶模型的闭环控制Bode图Fig.5 Close-loop Bode diagram of order-reduced model

图6 输出滤波器结构Fig.6 Structure of output filter
对于图6所示的输出滤波电路,若在电容支路串联阻尼电阻R,那么输出电流ips到输入电压uo之间的传递函数为:
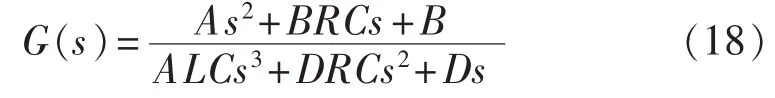
其中,A=L1L2+L1Lm+L2Lm,B=L2+Lm,D=LL2+LLm+L1L2+L1Lm+L2Lm。
由式(18)易知,系统的无阻尼振荡角频率为:

阻尼电阻上的损耗近似为:


图7 阻尼比与基波功率损耗之间的关系Fig.7 Relationship between damping ratio and fundamental power loss
图7给出了阻尼与损耗之间的关系,由图7、式(21)和式(22)不难发现:当电阻越大时,系统阻尼也越大,而损耗随ξ先增后减,当阻尼ξ=31.85时,阻尼电阻具有最大的损耗35.34 W。然而,电阻越大其体积和成本也越大。针对本文所提拓扑,取阻尼电阻R=4 Ω,对应的阻尼比为0.4,损耗约为0.89 W。
1.4 无锁相环指令电流生成算法
为了实现MGI对并网功率的跟踪和对谐波、不平衡以及无功电流的补偿,需要设计相应的指令电流生成算法。
文献[21]分析表明:基于锁相环的谐波电流检测算法在电网电压谐波或不平衡、控制延迟等条件下会对检测结果产生较大的影响,并提出了一种适用于硬件延迟补偿的无锁相环电流检测算法,较好地解决了补偿电流的检测问题。
基于同步旋转坐标系的无锁相环检测思想,这里将进一步给出一种跟踪指令功率的参考电流生成算法。该算法可替代传统并网逆变器的功率控制外环,提高系统的动态响应能力,降低控制算法的复杂度。对于电压、电流u和i:

其中,Um和Im分别为电压、电流相量的幅值;φu和 φi为其对应的相位。选用式(25)所示的Park变换:

其中,θ=ωt+θ0,θ0为初相位,也即 dq 坐标系 d 轴与abc坐标系a轴之间的夹角,θ0可以是任意值。Cabc/dq的逆变换满足:易知变换后的电压ut为:

类似地,对于变换后的电流it,有:

设逆变器有功和无功给定输出分别为P和Q,不难发现[22]:
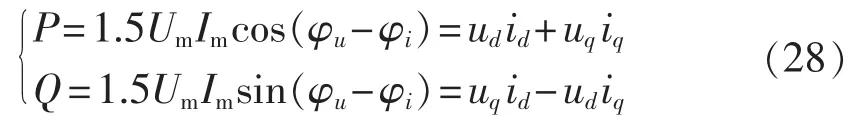
由式(28),并网功率跟踪电流可写为:

图8给出了MGI指令电流的生成算法框图。按图1所示电流参考方向,总的负荷电流iLabc可以由ioabc和isabc之和间接表示。其中,变换式T即式(29),生成的并网功率跟踪电流指令igabc和由文献[21]所提无锁相环补偿电流检测方法所检测出的补偿电流指令ihabc共同构成逆变器的指令电流irefabc,此外,ipabc为总负荷电流的正序基波有功分量,d、q为 PCC处电压的 d、q轴分量 ud、uq经过低通滤波器 LPF(Low Pass Filter)后的结果,变换式 Cpq为:

其中,ipd和ipq为dq坐标系下的总负荷电流正序基波有功分量。
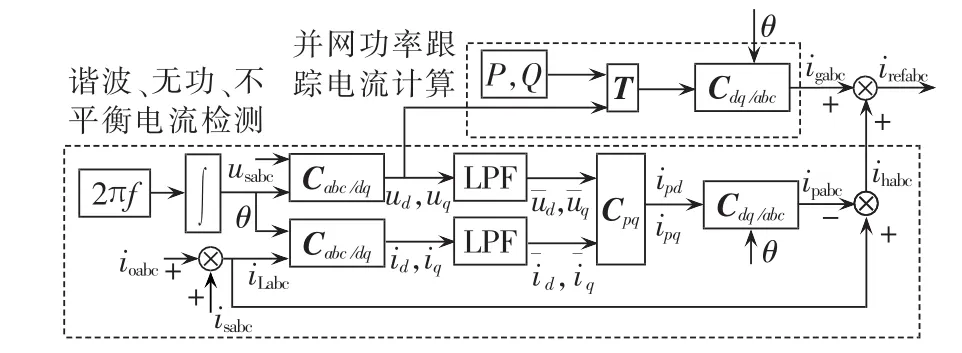
图8 参考电流生成算法框图Fig.8 Block diagram of reference current generation
需要说明的是,以上电流控制器设计中所采用的加权电流方法,只是对滤波器及隔离变压器漏感的原边等效电路进行了数学意义上的零极点对消和物理意义上的简化。但从隔离变压器的副边看进去,其副边电流和等效的加权电流之间仍满足变压器的匝比变换关系[23],即从加权电流的角度来看,电流参考信号的实际目标值和控制器的参考值仍然是一致的。故以上电流参考生成算法可以用作对虚拟电流进行调节,进而实现对多功能并网逆变器输出电流ioabc的控制。
2 仿真分析
为了验证图1所提拓扑及前述控制策略的正确性,利用PSCAD/EMTDC分别对多功能并网逆变器补偿不平衡和无功电流、谐波电流进行了仿真研究。
2.1 不平衡和无功电流补偿
在图1所示拓扑中将非线性负荷支路断开,MGI在实现并网功率跟踪的同时对PCC处不平衡电流和无功电流进行治理。不平衡负荷的各相参数为:a相为70Ω电阻负载,b相为40Ω电阻和118μF电容串联负载,c相为50 Ω电阻负载。并网功率指令值为P=15 kW、Q=0 var。MGI从0.15 s开始对网侧电流进行治理。功率器件的开关频率fs=10 kHz,系统参数同1.2节所述。
网侧电流和网侧功率如图9所示。当MGI不进行补偿时,由于不平衡负荷的原因,有功和无功功率以2倍频波动[24],且由于容性无功负荷的存在,网侧无功功率存在一个负的直流分量。当MGI投入补偿后,网侧电流三相对称,且功率波动得到很好的抑制,网侧无功接近0。可见,MGI在实现并网功率跟踪的同时,还能很好地完成对网侧无功和不平衡电流的治理,提高PCC处的电能质量。

图9 MGI补偿不平衡和无功电流的仿真结果Fig.9 Simulative results of unbalance and reactive currents compensation by MGI
2.2 谐波电流补偿
在图1所示拓扑中将不平衡负荷支路断开,MGI在实现并网功率跟踪的同时,完成对PCC处谐波电流的治理。非线性负荷的直流电阻为Rr=50 Ω,并网功率指令值为P=15 kW、Q=0 var。MGI从0.15 s开始对网侧电流进行治理。
网侧电流和网侧功率如图10所示。若不对网侧电流进行治理,非线性负载电流和并网电流的叠加将引起网侧电流波形畸变,反映在网侧功率上即为功率振荡。MGI投入补偿后,能明显消除电流波形畸变和网侧功率振荡。
不难发现,多功能并网逆变器在完成常规并网逆变器实现可再生能源或储能等微电网并网的同时,还兼有补偿PCC处无功、不平衡和谐波电流的能力,这使得一套并网逆变器能同时完成多个相互独立的功能,从而省去了额外的电能质量治理装置,在分布式发电系统和微电网中具有较好的应用前景。


图10 MGI补偿谐波电流的仿真结果Fig.10 Simulative results of harmonic current compensation by MGI
3 实验结果
为了进一步验证所提拓扑和控制策略的正确性,搭建了一台15 kV·A的MGI实验室样机。其拓扑如图1所示,控制策略如图4和图8所示,控制器选用TI公司的TMS320F2812 DSP芯片,系统参数与仿真条件相同。
图11给出了对不平衡和无功电流的补偿效果,图12给出了对谐波电流的补偿效果,图中点划线左、右侧分别为补偿前、后波形。对比实验结果和仿真结果可以看出,两者比较吻合,多功能并网逆变器在完成并网功率跟踪的同时,还能较好地实现对不平衡、无功和谐波电流的补偿,从而改善并网点处的电能质量。值得指出的是,虽然前面所提无锁相环参考电流生成算法能降低控制复杂度提供动态响应能力,但是无法克服滤波电容所产生少量容性无功对网侧功率的影响,加之电网电压波形也存在一定的畸变和不对称,共同使得补偿后的网侧无功稍小于0 var,且有功和无功存在小幅值波动。

图11 MGI补偿不平衡和无功电流的实验结果Fig.11 Experimental results of unbalance and reactive currents compensation by MGI

图12 MGI补偿谐波电流的实验结果Fig.12 Experimental results of harmonic current compensation by MGI
4 结论
本文针对一种多功能并网逆变器拓扑及其控制进行了研究,建立了其数学模型,设计了其控制器,给出了指令电流的生成算法和输出滤波器中阻尼电阻的设计。仿真与实验结果验证了所提拓扑及其控制策略的正确性和有效性。所提拓扑对直流电压要求较低,且在实现并网功率跟踪的同时,能有效治理谐波、无功和不平衡电流,尤其是在分布式发电系统和微电网电能质量治理中具有很好的应用前景。
