多机电力系统间接自适应模糊分散H∞控制研究
2013-10-23吴忠强宋明厚付立元
吴忠强,宋明厚,付立元
(燕山大学 工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)
0 引言
电力系统规模的不断扩大带来了一系列影响电力系统运行稳定性的新因素,改善与提高电力系统运行的稳定性有重要意义,而发电机的励磁控制是改善电力系统稳定性经济而有效的手段之一。
在传统的励磁控制研究中具有代表性的PID控制、电力系统稳定器(PSS)以及线性最优励磁控制(LOEC)都是基于某一平衡状态的近似线性化模型,只适用于改善小干扰稳定性问题[1]。随着电网规模的不断扩大,电网结构越来越复杂,电力系统中的非线性因素也越来越多[2],因此非线性控制方法将在电力系统中起着越来越重要的作用。无源化控制[3-5]、滑模控制[6-7]、自适应控制[8-10]、神经网络[11-12]等众多非线性控制已经应用到电力系统控制中。
自适应模糊逻辑系统可在任意精度上逼近定义在致密集上的非线性函数。文献[13]提出了直接和间接自适应模糊控制方法,但是该方案的监督控制项设计复杂且取值很大,最小逼近误差平方可积的条件也较苛刻,实际应用困难。文献[14-15]对文献[13]进行了改进,但是文献[14]不适用于间接自适应模糊控制,且控制器不具有鲁棒性;文献[15]利用滑模变结构结合模糊理论设计了控制器,但是滑模控制存在的抖振问题限制了该方案的应用。
本文针对多机电力系统,提出了一种间接自适应模糊分散H∞控制方案。该方案利用模糊逻辑系统逼近系统的未知函数,依据Lyapunov稳定性理论得到自适应律,使得模糊逻辑系统达到最优。在此基础上结合H∞控制理论设计补偿器,将建模误差和外部干扰控制在期望指标之内,无需设计复杂的监督器,仿真结果表明了该方案的有效性。
1 系统模型描述
考虑励磁控制的n台发电机组可用以下多变量非线性模型描述[16]:

其中,下标 i(i=1,2,…,n)为机组编号;Idi为第 i组电枢电流的d轴分量(标幺值);δi为第i机组转子运行角(rad);ωi为第 i机组角速度(rad/s);Pmi为第 i机组的机械功率(标幺值);Di为第i机组阻尼系数(标幺值);E′qi为第 i机组同步机暂态电势(标幺值);Efi为第i机组励磁绕组折算到定子侧的电势(标幺值);Xdi、X′di为第 i机组同步电抗和暂态电抗(标幺值);T′di为第i机组定子开路时励磁绕组时间常数(s);Hi为第 i机组转动惯量(s);Gii和 Yii分别为第 i节点的电导和导纳(标幺值);Gij、Yij分别为第 i和第 j节点之间的电导和导纳。
将式(1)写成如下形式:
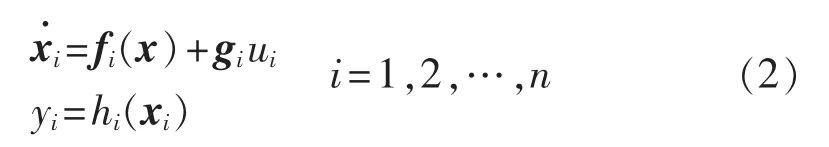

其中,xi∈R3为第 i个子系统的状态变量,ui∈R 为输入,yi∈R 为输出,fi、gi∈R3和 hi∈R 为光滑非线性函数。
2 间接自适应模糊分散H∞控制器设计
2.1 多机电力系统的状态变换
多机电力系统式(2)有一致相关度{3,…,3},即对每一个子系统均有相关度ri=3。
令:
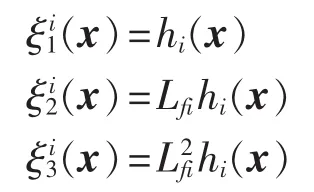
选择坐标变换z=Γ(x)为:

则可将系统式(2)化为如下形式:
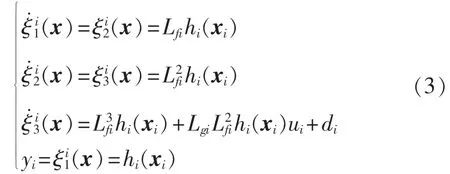
把上式化成输入输出形式:

给定参考输出 ymi,假设均为有界可测的。定义第i个子系统的跟踪误差ei0=ymi-yi。令其中 Ki使多项式稳定。
2.2 控制器设计
自适应模糊逻辑系统具有一致逼近性,能够在任意精度上逼近一个定义在致密集上的连续非线性函数。
定义模糊规则如下。
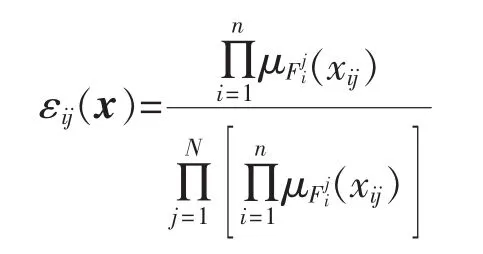
同理可对 βi(xi)建立模糊规则。
对于多机电力系统式(2)在 αi(xi)和 βi(xi)都是已知的情况下可取分散控制:

在 αi(xi)和 βi(xi)都是未知的情况下,首先利用模糊逻辑系统构造和来逼近未知函数 αi(xi)和 βi(xi)。 其形式如下:

其中,θ1i和 θ2i为自适应参数。

由于建模误差和外部干扰的作用,控制器式(6)不能很好地完成控制任务。因此,采用H∞补偿器uc来补偿外部扰动和逼近误差,则设计控制器为:

将设计的控制器式(7)代入式(4)中得误差动态方程为:
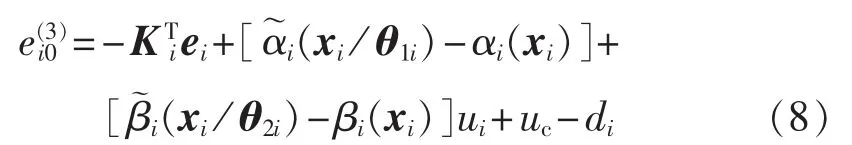
则式(8)等价于:


2.2.1 设计自适应律
首先定义 θ1i、θ2i的最优估计参数为

然后定义第i个子系统的模糊最小逼近误差为:

令 w1i=wi-di,参数误差向量则式(9)可化成:

选取Lyapunov函数为:
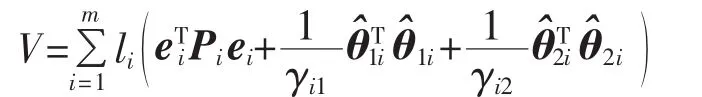
沿式(11)求V对时间的导数得:

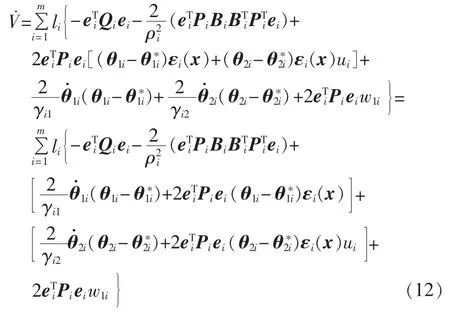
设计参数自适应律为:
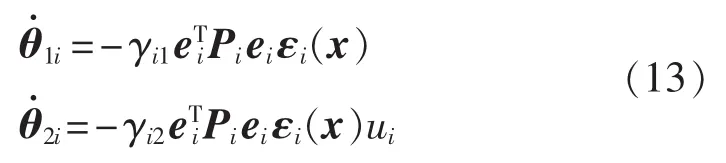
2.2.2 H∞性能指标的实现
将自适应律式(13)代入式(12)中得:

对式(14)从t=0到t=T积分得:

由于 V(T)≥0,所以可得:

即实现了H∞性能指标。
3 仿真研究
以由2台发电机组成的互联系统为例,考虑输电线路上存在的2种短路故障情况:一种是在20 s时在1号发电机和2号发电机联络线靠近1号发电机的输电线送端发生瞬时三相对地短路故障,在20.5 s时故障消失;另一种是在20 s时在1号发电机和2号发电机联络线靠近1号发电机的输电线送端发生永久性短路故障,20.5s时1号机被切除。
发电机参数如下 :H1=23.64 s,H2=6.4 s,Xd1=0.146 p.u.,Xd2=0.895 8 p.u.,X′d1=0.060 8 p.u.,X′d2=0.119 8 p.u.,D1=0.31 p.u.,D2=0.535 p.u.,Pm1=0.7157 p.u.,Pm2=1.6295 p.u.,T′d1=8.96 s,T′d2=6 s。

给定跟踪参考输出为ym1=ym2=1,给定正定矩阵Qi=diag[10 10 10],选取 Ki=[1 2 1]T,λi=0.01,解得:
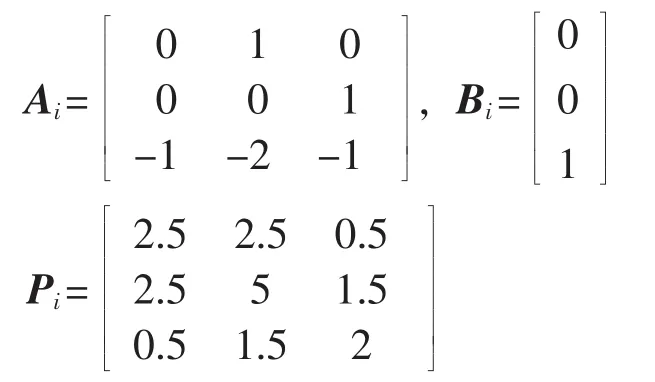
其中,i=1,2。
首先对于系统转子运行角δi和相对转速ωi-ω0(即 xi1,xi2)对建立模糊规则。

同理可得:
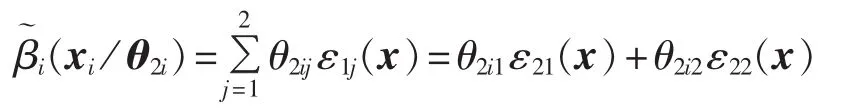
其中,i=1,2。 选择自适应律式(13),代入到控制器式(7)中,对比本文方案和PSS方案,可得仿真结果如下。
设20 s在1号发电机和2号发电机联络线靠近1号机母线处发生三相可恢复短路故障,在20.5 s时故障消失。转子运行角δi、发电机转子与同步转速之间的相对转速ωi-ω0以及跟踪误差的仿真结果如图1—6所示。

图1 转子运行角δ1曲线Fig.1 Curves of rotor operational angle δ1
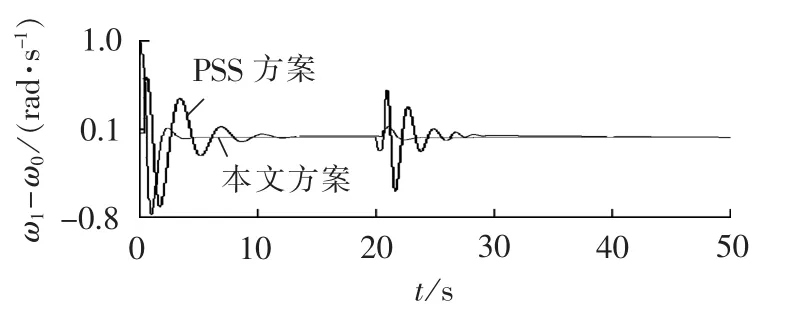
图2 相对转速 ω1-ω0曲线Fig.2 Curves of relative angular velocity ω1-ω0

图3 转子运行角δ2曲线Fig.3 Curves of rotor operational angle δ2
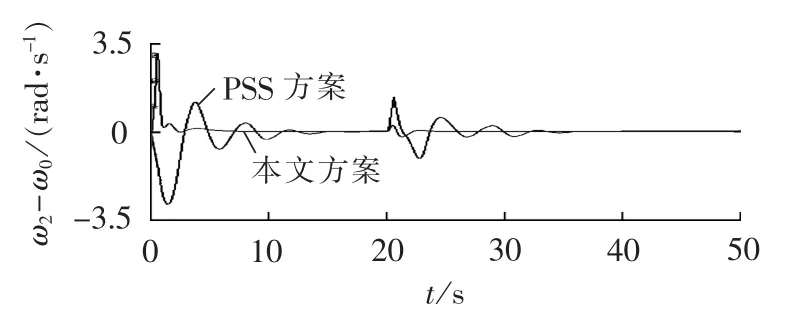
图4 相对转速ω2-ω0曲线Fig.4 Curves of relative angular velocity ω2-ω0

图5 跟踪误差e1曲线Fig.5 Tracking error of e1

图6 跟踪误差e2曲线Fig.6 Tracking error of e2
设20 s在1号发电机和2号发电机联络线靠近1号机母线处发生三相不可恢复短路故障,20.5 s时1号机被切除。转子运行角δi、发电机转子与同步转速之间的相对转速ωi-ω0以及跟踪误差的仿真结果如图7—12所示。
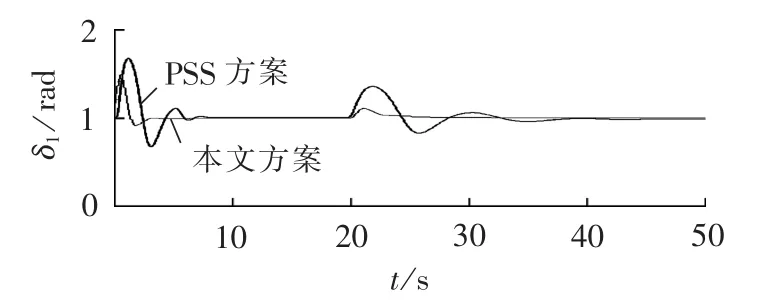
图7 转子运行角δ1曲线Fig.7 Curves of rotor operational angle δ1

图8 相对转速ω1-ω0曲线Fig.8 Curves of relative angular velocity ω1-ω0

图9 转子运行角δ2曲线Fig.9 Curves of rotor operational angle δ2
仿真结果表明,当多机电力系统发生三相可恢复故障和三相不可恢复故障时,发电机的转子运行角趋于某一固定值,而相对转速和跟踪误差都趋于零。本文方案与PSS方案对比可得,PSS方案虽然能使系统稳定,但是其超调量大、过渡时间长;本文方案不仅可以使系统在故障之后迅速稳定,而且超调量更小,从而表明了本文方案的优越性。

图10 相对转速ω2-ω0曲线Fig.10 Curves of relative angular velocity ω2-ω0

图11 跟踪误差e1曲线Fig.11 Tracking error of e1

图12 跟踪误差e2曲线Fig.12 Tracking error of e2
4 结论
本文针对多机电力系统的多变量、强耦合等非线性特点,提出了一种间接自适应模糊分散H∞控制方案。该方案利用模糊逻辑系统逼近系统的未知函数。依据Lyapunov稳定性理论求得自适应律,使得模糊逻辑系统达到最优。在此基础上结合H∞控制理论设计补偿器将建模误差和外部干扰控制在期望指标之内。两机电力系统的仿真结果表明了该方案的有效性。
