未覆土高陡边坡输气管道的应力分析

蒋 喜 王棠昱 孙 蔺 吴 瑕

1.中国石油集团工程设计有限责任公司西南分公司，四川 成都 610041；2.西南石油大学石油工程学院，四川 成都 610500

0 前言

随着我国管道建设的发展，长输油气管道不可避免的通过地形陡峭的局部山区［1］。敷设在高陡边坡上的埋地输气管道，若管土间的相互摩擦力不能与管道的重量载荷相平衡，将会使边坡上的管道沿坡道下滑。一般而言，未覆土的高陡边坡管道，由于缺少顶端覆土的摩擦阻力，极易形成管道下滑，是高陡边坡管道最危险的特殊边界情况。但是目前，对高陡边坡管道的应力及位移研究主要集中于边坡稳定性或滑坡后的失效分析［2-4］。因此，对高陡边坡上的未覆土输气管道进行应力分析研究十分必要。美国COADE公司的CAESAR II，是基于3D梁模型的应力分析专业软件［5］，可通过合理的工况设置准确的模拟非线性载荷［6-7］。本文基于CAESAR II软件，建立了高陡边坡未覆土管道的应力分析模型，研究了约束条件和边界条件的设置方法，讨论了加载工况和应力校核标准，并通过计算实例验证了模型的可行性。

1 管道模型的建立

长期实践和工程应用证明，对于管径与壁厚之比小于100的管道，采用梁单元的精度已足够［8］。因此管道主体采用3D梁单元模型进行模拟，3D模型中定义各坐标方向：

a）轴向为平行于管道轴线方向，对应坐标轴x；

b）纵向为垂直于管道轴线方向，当管道水平时与重力方向平行，对应坐标轴y。

c）横向为垂直于管道轴线方向，当管道水平时垂直于重力方向，对应坐标轴z。

3D模型中定义各坐标方向见图1。

图1 各坐标方向的定义

管道中的弯头同样采用梁单元模型，但是考虑到弯头处因扁率所导致的应力集中，因此特别引入了应力增强系数（Stress Intensification Factor，简称SIF），来考虑弯头处的应力集中效果。作为埋地输气管道，SIF的计算参照美国ASME B31.8《输气和配气管道系统》标准的附录E［9］。 建模过程中的管道承压则作为均布载荷加载于管道内壁，除此外还应计入压力荷载所带来的玻尔登效应。

由于梁模型默认将重量均分给两端的2个节点，因此在划分管段网格时，若节点距离过大，将导致过多的重量错误的集中于节点处，使应力校核无法通过。因此，文献［6］建议在建模中：凡是由地面支承的直径大于300 mm的管道，节点之间的距离应小于等于20倍的管道直径；而直径小于等于300mm的管道，节点之间的距离则应大于30倍管道直径。

2 约束与边界条件

2.1 土壤约束

未覆土的管道横卧在管沟中，其管底与土壤连续接触，侧边与管沟壁接触，管道与管沟作用，其受力：

a）轴向：因管底与土壤连续接触，因此受到土壤的摩擦力作用。

b）横向：受到横向制止约束，并产生轴向摩擦力。

c）纵向：管道受土壤向上的支承力作用，不会产生垂直土壤面向下的运动。

以上土壤作用可以表达为：

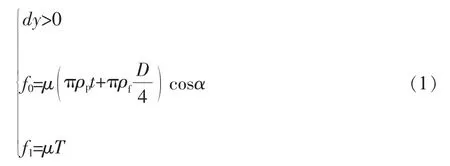
式中：dy为管道在纵向上的位移，m；f0为单位长度管道上因重力而产生的摩擦力，N；f1为单位长度管道上因横向推力而产生的摩擦力，N；D为管道外径，m；μ为土壤与管壁之间的摩擦系数［10］，按表1取值；α为坡道倾角，管道水平时取0°，管道竖直时90°，deg；ρp为钢管密度，kg/m3；ρf为管内流体的密度，kg/m3；T为管道所受横向推力，N。

在CAESAR II中，这一约束设置的方法见图2。

图2 CAESAR II中的约束设置

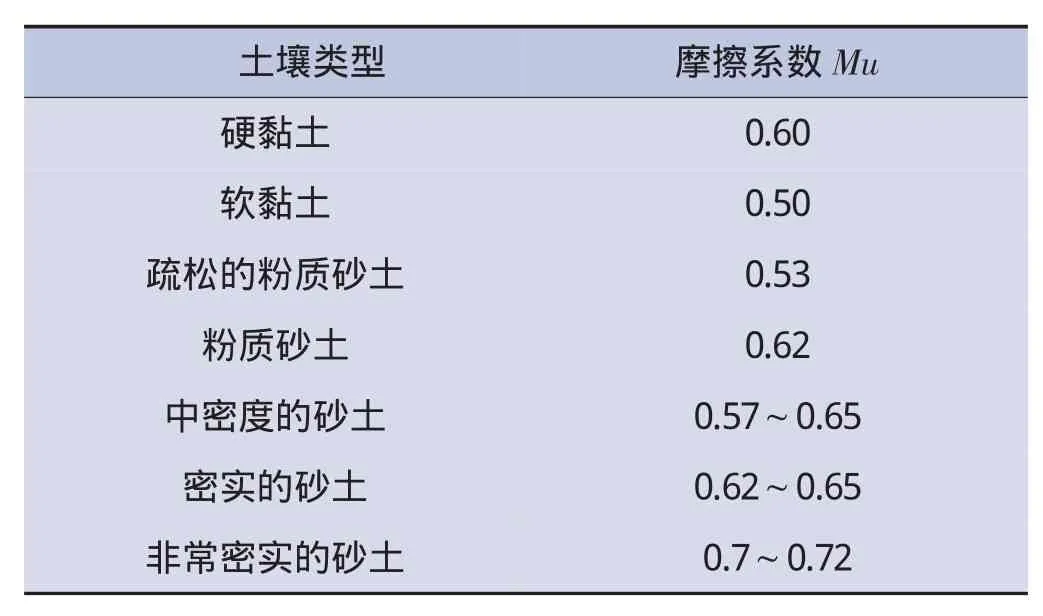
表1 土壤与管壁之间的摩擦系数

2.2 边界条件

根据未覆土高陡边坡输气管道的实际情况，有三种方法可以简化边界条件。一是管道在坡道两端，即坡道的底部和顶部立即结束，并设定为自由边界；二是根据断层边界理论[11]，认为坡道之外的管道将不受坡面管道移动的影响，将管道在坡道两端处立即结束，并设定为固定边界；三是综合以上两方面，将管道在坡道两端各延长一定距离，再设定为固定边界。三种边界条件见图3，在实际建模时，自然边界和固定约束边界在坡道两端均只增加1个管段节点。

图3 验证模型的边界条件

为了验证不同边界对模型的影响，采用CAESAR II建立了某管道的应力分析模型。管道规格为Φ1219mm×26.4mm，管段坡面总长650m，坡度为55°。向管道内加载水的自重与15MPa的水试压压力后，得到管道在三种边界条件下的轴向及纵向位移见图4～5，位移方向的规定见图1。

三种边界条件下的计算结果表明，整条管道都存在轴向位移，这是由非嵌固管道的热胀效应所产生的。管道的轴向位移沿坡道先增大后减小，表明管道沿坡道下滑的趋势同时受到坡道两端即坡底和坡顶管道的制约。管道的纵向位移与轴向位移的趋势相同，不同之处在于管道两侧出现了纵向位移为0的情况，这是由于建模管道在坡底和坡顶都是水平管段，因此虽然存在轴向位移，但管道实际沿水平方向移动，并没有纵向位移。

图4 不同边界条件下的轴向位移

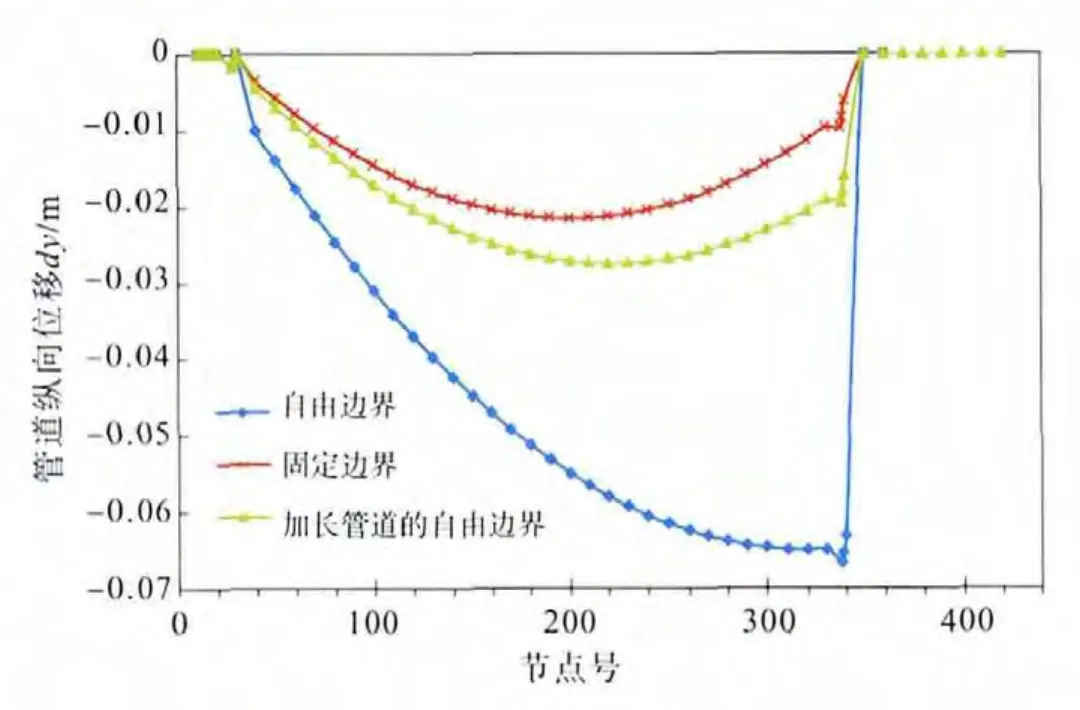
图5 不同边界条件下的纵向位移

分析计算结果可知：自由边界管道在轴向和纵向上均出现了远大于另两类边界的位移。主要原因是忽略了坡顶和坡底管道对坡道上管道的约束作用。而事实上，边坡两端所连接的管道可以通过管土间摩擦力来平衡坡道上管道的重力。因此，自由边界条件忽略这一阻力作用所形成的大位移是不合理的。

另一方面，添加固定约束边界与加长管道的自由边界在变化趋势上是一致的。但加长管道的位移极值较大，且出现极值的位置更靠后。这一现象是坡道管段位移带动相邻管道移动而出现的，在固定约束边界中，无法表达这一移动。因此，加长管段的固定边界条件是未覆土高陡边坡输气管道的最佳简化边界条件。

R.P.Kennedy于1977年提出断层边界理论，指出即使在断层错动这样的大变形条件下，管土之间存在较大相对位移的范围只有十几米到三十米左右。为了保证计算的准确性，规定直径大于300mm的管道，加长距离应不小于200倍的管道直径；而直径小于等于12 in.（DN300）的管道，加长距离不应小于300倍管道直径。

3 加载条件与校核标准

未覆土的高陡边坡管道在水试压过程中所受到的基本载荷，见表2。

在管道的应力分析中，未覆土管道应视作非嵌固管道。根据ASMEB31.8的相关规定，一次、二次应力均应进行校核，需考虑的组合工况及其校核标准见表3。

表2 管道所受基本载荷

表3 组合工况与校核标准

应注意在计算热应力时采用L2-L3而非直接使用T1，其主要的原因是当管道存在非线性约束时，单独加载T1与采用OPE-SUS间的位移结果可能发生反向。为了保证求解结果的准确性，CAESAR II一般在求解EXP工况时采用OPE-SUS的组合工况。

未覆土的管道在水重及水压的共同作用下，可能被拉动下滑。因此，当管道中的一次、二次应力满足要求后，还要对管道的轴向和纵向负位移进行校核。

4 应用实例

某天然气输送管道规格为Φ406.4mm×14.3mm，材料为L360，管道总长626m，落差248m，最大坡度达61.58°。管内介质密度为80 kg/m3，所在地区等级为一级，安装温度10℃，运行温度20℃，运行压力10MPa，水试压压力为15MPa。根据管道基本信息及安装图，在管道两侧添加了加长管道后的固定边界。基于CAESAR II所建成的分析模型见图6，计算得到的各工况条件下的应力和位移极值见表4。

由表4可知，水试压条件下的应力极值远大于其它加载工况。为了进一步分析水试压条件下管道应力的变化趋势，特将该工况下的应力值进行排序，表5为应力最大的5个节点数据。

图6 建成的未覆土高陡边坡模型

表4 各工况条件下的应力和位移极值

表5 水试压条件下的应力计算结果

本实例中管道的最大轴向位移为-4.42 cm，最大纵向位移为-1.92 cm（位移方向的规定可见图1）。管道的最大位移出现在节点281处，位于管道最长且最陡峭边坡的顶端，见图7。

综合管道走向与应力、位移校核结果，可以得出：

a）管道在未覆土条件下的各工况中没有出现应力超限的情况，其中应力最大的为水试压工况，最大应力值占许用应力的60.7%，最大应力节点为139，位于坡底平台与下一段下坡管道的弯头处。

b）根据表5可知，水试压条件下的最大应力位置均为弯头处，但其应力值的大小并不只取决于弯头的角度，还与前后连接的管道是否水平及坡道长短有关，因此最大角度的坡道弯头并不一定是最大应力点。

c）管道的最大轴向位移为-4.42 cm，最大纵向位移为-1.92 cm。管道的最大位移出现在节点281处，位于管道最长且最陡峭边坡的顶端，由此可见，边坡顶的管道是位移最大。

图7 节点281所在位置

5 结论

针对未覆土条件下高陡边坡上天然气管道的实际情况，提出了该类管道的应力分析模型。通过比选三类不同的简化边界条件，确定将坡道两侧有水平增长段的固定约束作为模型的边界条件。建立了四种加载工况，分别为水试压工况、操作工况、持续工况和热应力工况，并基于美国ASMEB31.8标准的要求提出了各类工况的校核方法。通过计算实例验证了应力计算模型和校核方法的可行性。

［1］吴 宏，李 波.西气东输工程隧道内管道施工新方法［J］.油气储运，2003，2（6）：47-52.W u Hong，Li Bo.Latest Methods Used to Build the Pipe in Land Tunnelsin W est-EastGasProject［J］.Oil&GasStorage and Transportation，2003， 2（6）:47-52.

［2］王芝银，袁鸿鹄，王 怡，等.管道穿越土质边坡斜竖井设计参数的确定方法［J］.中国石油大学学报 （自然科学版），2010，34（1）： 105-108.Wang Zhiyin，Yuan Honghu，Wang Yi，et al.New Method of Determining Design Parametersof Inclined Shaft for Oil-Gas Pipeline Crossing Along Soil Slope ［J］.Journalof China University of Petroleum（Edition ofNaturalScience），2010，34（1）:105-108.

［3］俞火明.杭-甬天然气管道沿线某高边坡稳定性分析与加固方案评价［J］.中国港湾建设，2011，176（5）： 47-50.Yu Huom ing.Stability Analysisand Reinforcement Scheme of aHigh Slopealong Hang-Yong NaturalGasPipeline［J］.ChinaHarbour Engineering， 2011， 176（5）:47-50.

［4］周晓莹，郭永华，吕晓华，等.地质滑坡条件下不同因素对油气管道危险性影响分析［J］.工业安全与环保，2012，38（5）：42-44.Zhou Xiaoying，Guo Yonghua，Lv Xiaohua，etal.Study on Effect of Different Factorson Pipelines Risk under Landslide［J］.Industrial Safety and Environmental Protection， 2012， 38（5）:42-44.

［5］龙忠辉.CAESARⅡ管道应力分析软件开发应用［J］.化工设备与管道，2001，38（3）：50-54.Long Zhonghui.Developmentand Application of Piping Stress AnalysisSoftware CAESAR Ⅱ ［J］.ProcessEquipment&Piping， 2001， 38（3）:50-54.

［6］GeorgeM.管道应力分析理论指南［M］.王 昕，译.COADE Inc中国技术服务与培训中心，1998.22-27.George M.Pipe Stress Analysis Theory Guide［M］.COADE Inc China Technical Service and Training Center，1998.22-27.

［7］Stumpf P D，Ainsworth H A，Appleton R A，et al.Technical ReferenceManual［M］.COADE Inc Press，2003.128-221.

［8］Audibert J，Nyman K.Coefficients of Subgrade Reactions for the Design of Buried Piping ［C］.2ndASCESpecialty Conference on Structure Design of Nuclear Plant Facilities，LA，1975.235-244.

［9］Nance A D，Hayden L E，Stumpf PD，et al.B31.8-2010 Gas Transm ission and Distribution Piping Systems［S］.The American Society ofMechanicalEngineersPress，2010.21-27.

［10］帅 健，于桂杰.管道及储罐强度设计［M］.北京：石油工业出版社，2006.10-11.Shuai Jian，Yu Guijie.Stress Design for Pipelines and Tanks［M］.Beijing:Petroleum Industry Press， 2006.10-11.

［11］KharaitiL，George M，Nyman D J.GuidelinesFor the Seism ic Design of O il and Gas Pipeline System ［M］.The American Society ofCivilEngineersPress，1984.70-77.