基于各向异性高斯核方向导数滤波器的图像轮廓检测*

陈雅静，刘 桥，周 骅，张泽均

（1．贵州大学 理学院，贵州 贵阳 550025;2．西安电子科技大学 电子工程学院，陕西 西安 710071）

0 引言

在计算机视觉和图像处理中，对象的轮廓携带了对象形状的重要信息，它是基于图像和视频的目标识别、目标跟踪和三维重建的基础［1］。轮廓检测就成了必须解决的问题，它的任务是定位图像中对象的边缘，目的是为了增强机器理解现实世界的能力。常用的轮廓检测方法有基于梯度的 Roberts 算子［2］、Prewitt算子［3］和 Sobel算子［4］;基于二阶导数 Laplacian 算子［5］、Marr算子［5］和 Canny算子［6］。其中，检测性能最优秀的是Canny算子。

Canny检测算子［6］利用各向高斯核函数对图像进行滤波来降低图像中的噪声对检测结果的影响。为了在检测结果的分辨率与噪声抑制之间寻找折中，高斯核函数的尺度因子不能选的太大或者太小。Canny检测结果中，在真实轮廓周围存在大量的毛刺，而且存在大量由纹理引起的虚假轮廓。

最近，各向异性高斯核函数及其方向导数被用于图像轮廓检测［7］，文献［7］将各向同性高斯核函数与各向异性高斯核函数相结合，获得了较好的检测性能。但该方法的检测结果中仍然存在许多毛刺与虚假轮廓。

本文基于各向异性高斯核方向导数滤波器和图论方法，提出一种新的图像轮廓检测算法。利用各向异性高斯核方向导数滤波器捕捉图像中的方向变化信息，使用与文献［6］中相同的阈值化处理方法来获得图像的初始轮廓检测结果。将初始检测轮廓检测结果转换成无向图表示，利用图论中提取最短路径的方法递归地将初始检测的轮廓转换成简单轮廓集合（只有2个端点的轮廓），然后使用简单的阈值化处理方法消除初始轮廓检测结果中的毛刺与虚假轮廓。将本文方法的检测结果与广泛使用的Canny检测方法相比，本文方法获得更好的检测性能，能更好地提取真实轮廓，而且基本消除毛刺，大大减少了虚假轮廓。

1 各向异性高斯核与各向异性高斯核方向导数

1．1 各向异性高斯核

将高斯核函数在x轴上压缩一定的比例ρ，同时在y轴上拉伸同样的比例ρ，得到各向异性的高斯核函数［7］

式中 ρ为各向异性因子，σ为尺度因子，x=［x y］T为平面坐标。将各向异性高斯函数（1）旋转角度θ，得到一组各向异性高斯核函数

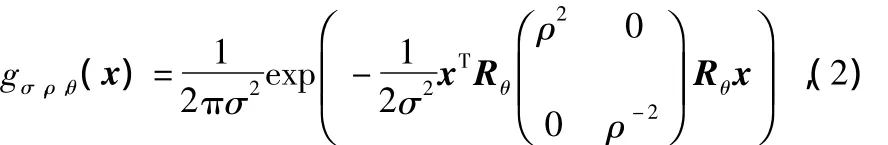
式中 Rθ为旋转矩阵，且

1．2 各向异性高斯核方向导数滤波器

对式（2）中的各向异性高斯函数在θ方向上求方向导数，得到θ方向上的各向异性高斯核方向导数滤波器

图1中给出了16个方向上的各向异性方向导数滤波器。各向异性方向导数滤波器有2个优点:1）它继承了高斯核对噪声的平滑作用，它对噪声的平滑作用只与滤波器的尺度因子σ有关，而与其他的2个参数无关［7］;2）它可以提取图像在各个方向上的变化信息。

2 图像轮廓检测算法

利用各向异性高斯核方向导数滤波器提取图像的各个方向上的变化信息，构造图像的边缘强度映射（edge strength map，ESM）。使用固定的高低阈值在ESM中提取图像的候选轮廓，得到初始的轮廓检测结果。利用图论方法提取初始检测结果中的主轮廓集合，结合各向异性高斯核方向导数滤波器提取的图像的方向信息，消除初始轮廓检测结果中的毛刺和虚假轮廓，得到图像中对象的真实轮廓。

图1 各向异性方向导数滤波器，其中 σ2=4，ρ2=2，θk=kπ/16，k=0，1，…，15Fig 1 ANDDs filter，where σ2=4，ρ2=2，θk=kπ/16，k=0，1，…，15

2．1 初始轮廓检测

利用各向异性高斯核方向导数滤波器对原始图像进行卷积，提取图像的各个方向的变化信息，卷积的计算公式如下

其中，I（x）为图像，*表示二维卷积运算。Gg（x，θ）为x点在θ方向上的变化信息。

将式（4）中获得图像的各个方向上的变化信息组合在一起，得到

很显然，在轮廓附近，Gg（x，θ）的值比较大，而在平坦区域或者灰度变化缓慢的区域，Gg（x，θ）的值比较小。这样，使用与文献［6］中相同的阈值化处理方法，就可以得到图像中轮廓的初始检测结果，即得到图像的候选轮廓。虽然式（4）中的各向异性高斯核方向导数滤波器对轮廓两边的噪声有一定的抑制作用，减少了噪声所引起的虚假轮廓，但由于高斯核自身的影响［8］，导致在对象轮廓附近存在大量的虚假轮廓和毛刺。同时，图像中存在的无关紧要的纹理也会导致大量虚假轮廓的产生。本文结合图论中的最短路径算法与各向异性高斯核方向导数滤波器的特性，来消除初始轮廓检测结果中的虚假轮廓与毛刺。

2．2 毛刺与虚假轮廓的消除

在图像初始轮廓检测结果中，由于高斯核在平滑图像中噪声的同时也会抬高真实轮廓附近像素点的Gg（x，θ）值，这些像素使得在轮廓检测结果中，存在较多的毛刺与真实轮廓相连，这种现象在弱的真实边缘上大量存在。另一方面，自然图像中往往存在无关紧要的纹理，这些纹理将产生大量不需要的虚假轮廓。因此，在图像的轮廓检测中，如何消除检测结果中存在的大量毛刺与虚假轮廓是一个非常重要的问题，也是一个难题。本文将初始检测的轮廓转换成无向图的表示，递归地提取该无向图中具有最大平均权值的路径，将该路径对于的轮廓称为简单轮廓（只有2个端点），利用阈值方法来消除具有较小平均权值的轮廓，得到最终的轮廓检测结果。

用无向图G=（V，E）来表示初始检测结果中的轮廓，V为节点集合，其中的每个节点对应于轮廓上的一个像素点。E为边集，如果i，j∈V，而且i∈Bj或者j∈Bi，Bi和Bj分别为像素点i和j的八邻域像素集合，那么，（i，j）∈E。在无向图G中，给每一个节点i一个权值w（i），权值w（i）为Gg（x，θ），x为节点i对应的轮廓像素点，θ为像素点x的近似轮廓方向。本文使用如下方法估计轮廓上像素点x的近似方向。首先，使用分段线段来近似表示轮廓;其次，提取与近似线段最近的离散方向;最后，将这个近似的方向作为该线段两端点之间轮廓上的像素的方向。本文使用递归细分的方法获得轮廓的分段线段表示，细分方法:连接轮廓上2个端点，成一条线段;找出轮廓上到该线段距离最长的点，如果这个最长距离小于该线段的0．25倍，停止细分该轮廓;否则，在该点处将线段分成2段，继续进行该过程。图2中显示了细分过程。

图2 直线表示的过程Fig 2 Procedure represented using lines

图3中显示了用无向图表示轮廓的例子。图3（a）为提取出来的一个轮廓，图3（b）为它的图表示结果，图中节点上的权值为其对应的像素在其轮廓方向上的变化信息。从图3（b）中可以看出:在轮廓的端点处的像素对应的图节点的度数为1。这些度数为1的节点是提取主轮廓时的开始节点或者结束节点。

图3 轮廓的图表示Fig 3 Graph representation of contour

为了消除虚假轮廓和毛刺，需要将初始检测的图像轮廓进行细分，将一个多分叉轮廓细分成多个没有分叉的轮廓（简单轮廓），细分的结果要求满足2个条件:1）细分出来的每个轮廓的2个端点在原始轮廓中均为轮廓的端点;2）提取出来的轮廓上，所有像素在其对应的方向上的变化信息的平均值最大。将初始检测的轮廓转换成图3所示的图表示，同时，将每个节点上的权值取负数，就可以使用图论中提取最短路径（the shortest path）的算法来递归地提取主轮廓，从而实现多分叉轮廓的细分。图4给出了递归地细分轮廓的算法流程图。

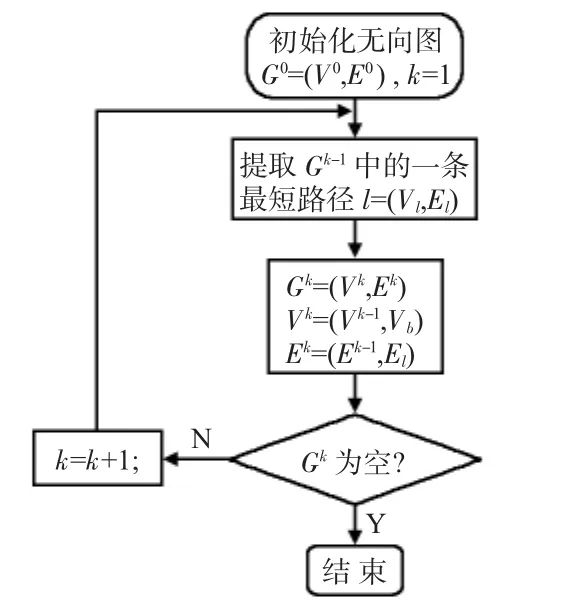
图4 轮廓细分流程图Fig 4 Flow chart of contour subdivision

对于由图4中的算法提取出来的每一个轮廓l=（Vl，El），计算这个轮廓的平均方向变化信息

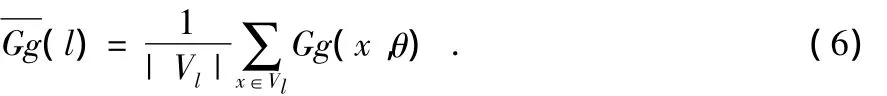
使用阈值化方法来判断图4中的算法提取的轮廓l是不是需要检测的轮廓

其中，T为阈值，轮廓判断函数is_contour（l）为1，表示l为需要检测的轮廓;否则，它为毛刺或者虚假轮廓，需要从初始检测轮廓中消除。

3 实验结果与分析

为了验证本文算法的有效性，将本文算法的轮廓检测结果与现在广泛使用的Canny算法［6］进行比较，本文的所有实验中，Canny算法所有参数设置均为Matlab中的最优设置。本文算法的所有参数设置均统一为:各向异性高斯核的尺度因子σ2为4，各向异性因子ρ2为2，旋转方向的采样数为 16，即方向分别为 θk=kπ/16，k=0，1，…，15。初始轮廓检测中的高低阈值为0．7和0．3。毛刺与虚假轮廓消除中的阈值T为0．45。

图5显示了本文算法的轮廓检测结果与Canny检测结果的比较。从图5中可以看出:本文方法有以下优点:1）本文方法的检测结果中，真实轮廓附近的毛刺基本给消除，大大减少了由于纹理引起的虚假轮廓;2）本文方法提取的轮廓更完整，与真实轮廓更匹配。

图5 没有噪声图像的轮廓检测结果比较Fig 5 Result comparison of contour detection on noise-free images

图6中显示了加入标准方差为10的高斯噪声图像的轮廓检测结果比较。从图6中的检测结果可以看出:本文算法在含有噪声的图像中也能提取出较好的轮廓。综上所述，本文提出的轮廓检测方法具有强的实用性。

图6 噪声图像的轮廓检测结果比较Fig 6 Result comparison of contour detection on noise image

4 结束语

本文基于各向异性高斯核方向导数滤波器，提出一种高效而实用的轮廓检测算法。使用简单的传统边缘检测方法来提取初始轮廓，将初始轮廓转换成无向图表示，利用图论中的最短路径算法递归地将初始轮廓细分成简单轮廓集合，然后，利用简单的阈值化方法消除初始轮廓检测结果中的毛刺与虚假轮廓。将本文方法的检查结果与广泛使用的Canny检测方法相比，验证了本文方法基本消除了噪声轮廓附近的毛刺，而且大大减少了由纹理引起的虚假轮廓。本文方法在噪声图像中也能检测出较好的结果。

［1］ Hu Weiming，Zhou Xue，Li Wei，et al．Active contour-based visual tracking by integrating colors，shapes，and motions［J］．IEEE Trans on Image Processing，2013，22（5）:1778 －1792．

［2］ Roberts L G．Machine perception of three-dimensional solids［M］．Cambridge:MIT Press，1965．

［3］ Prewitt J M S．Object enhancement and extraction［M］．New York:Academic Press，1970．

［4］ Sobel I E．Camera models and machine perception［D］．Palo Alto，Calif:Stanford University，1970．

［5］ Marr D，Hildreth E．Theory of edge detection［J］．Proc R Soc of Lond，1980，B207:187 －217．

［6］ Canny J．A computational approach to edge detection［J］．IEEE Trans on Pattern Analysis and Machine Intelligence，1986，8（6）:679－698．

［7］ Shui Penglang，Zhang Weichuan．Noise-robust edge detector combining isotropic and anisotropic Gaussian kernels［J］．Pattern Recognition，2012，45（2）:806 －820．

［8］ Basu M．Gaussian-based edge-detection methods—A survey［J］．IEEE Trans on Systems，Man，and Cybernetics，2002，32（3）:252－260．