基于模糊支配的生物地理学优化算法及其在含风电场电力系统调度中的应用

赵 简，龚庆武，陈道君，刘 栋

（武汉大学 电气工程学院，湖北 武汉 430072）

0 引言

除了各种新能源的并网运行之外，通过电力系统优化调度，调整不同机组间的负荷分配也是控制废气排放的有效手段之一。与提高传统化石燃料机组效率、加装脱硫处理装置等方法相比，电力系统优化调度具有不需要增加硬件、投资少、见效快的优势。因此，正确和高效地处理含风电场电力系统的优化调度是实现电力生产节能减排的有效手段之一。

传统电力系统优化调度问题考虑经济调度ED（Economic Dispatch）[1]，将发电成本作为单一目标。电力系统经济环境优化调度EED（Economic Environmental Dispatch）模型，在传统ED问题的基础上加入环境影响函数，构建电力系统经济环境双目标优化调度模型[2]。处理多目标优化问题的传统方法是赋权值策略，通过设定权重因子，将多目标问题转化为单目标问题求解[3]。这类方法的缺点在于过分依赖权重参数，需要多次优化寻找帕累托解集，无法求出非凸集中的解。另一种方法是使用帕累托最优的概念评价解的优劣[4]，即解间的支配关系，将优化目标转化为寻找一组符合评价标准的解。然而，原始帕累托最优的概念不仅无法评价互不支配的解的优劣，也不能表示某一解对另一解的支配程度，使用中非常不便。目前，解间支配关系的求解方法可分为NDS（Non-Dominated Sorting）[5]和 MOR（Multi-Objective Ranking）[6]2 种。然而 NDS 和 MOR 都依赖于被支配解的存在，当目标维数增加时，解集中含非支配解的概率大幅下降，对于解的区分度也会随之极大降低[7]。Farina和Amato提出使用模糊支配的方法求解解间的支配关系[8]。模糊支配的定义更接近支配的原始概念，在处理多目标函数的优化问题中具有更好的实用性。

求解优化问题的算法主要分为传统算法和启发式算法2种。后者中目前得到广泛研究和应用的有遗传算法（GA）[9-11]、进化规划算法[12]和粒子群优化（PSO）算法[13-15]等。 Dan Simon 在 2008 年提出一种新的启发式算法——生物地理学BBO（Biogeography-Based Optimization）算法通过模拟自然界不同栖息地种群数量的变化过程寻找优化问题的最优解。文献[17]的研究表明BBO算法在非凸性电力系统经济调度问题上比其他启发式算法具有更好的收敛性、更高的计算效率，所得解的质量更优。但目前BBO算法在电力系统的应用仅限于处理单目标优化模型。

本文提出基于模糊支配的生物地理学FDCBBO（Fuzzy Dominance-Combined Biogeography-Based Optimization）算法，使用模糊支配（fuzzy dominance）的方法计算解间的支配关系，然后用解间的支配关系代替BBO算法中的估价函数，并将其应用于含风电场电力系统双目标优化调度。实例验证表明，FDCBBO算法同使用同样支配算法的遗传算法（FDCGA）、粒子群算法（FDCPSO算法）相比，具有更好的计算性能。

1 含风电场的电力系统双目标优化调度模型

1.1 目标函数

1.1.1 含风电场电力系统发电成本目标

在含风电场电力系统中，采用风电全部优先并网策略，发电成本由火电成本和风电成本组成。火电成本主要是煤耗成本，而风电成本主要是风电场运行成本，分别如式（1）和式（2）所示。

其中，N 为运行火电机组的台数；ai、bi、ci、di、ei为第 i台火电机组的发电费用系数；PTi为第i台火电机组的有功功率输出；PT为由 PTi（i=1，2，…，N）组成的向量；PminTi为第i台火电机组的有功出力下限；Pw为风电场的等值出力；δ为风电场运行费用系数。

由式（1）和式（2）可得系统发电成本目标函数：

1.1.2 含风电场电力系统环境影响目标

电力生产过程中产生的CO2、SO2、NOx等有害气体给生态环境造成了严重的污染和破坏。本文采用环境影响因子y代表电力生产所产生废气排放总量（t／h）[18]：

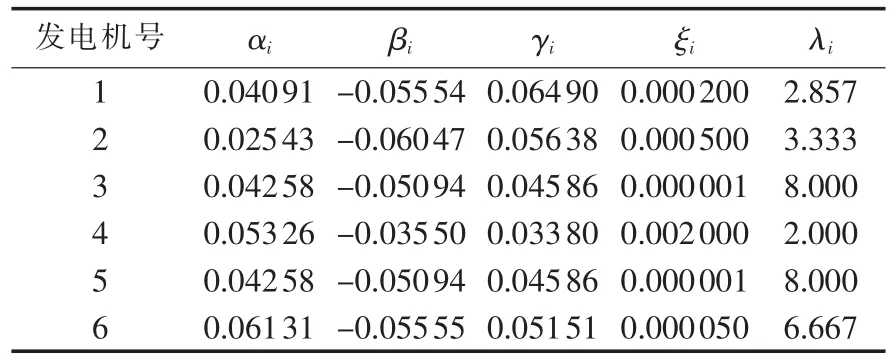
其中，αi、βi、γi、ξi和 λi为环境影响因子系数。

系统环境影响目标函数为：

1.2 约束条件

1.2.1 功率平衡约束

其中，Ploss为网损，PD为有功负荷。火电与风电机组总的有功出力应该能够平衡总负荷与线损之和，Ploss由Kron 公式计算[19]。

其中，Bij、B0i、B00为系统网损参数，Pi、Pj分别为第 i、j台机组的有功出力。

1.2.2 机组出力约束

在稳态运行中，机组有功出力满足上下限限制。

其中，PmTiax和PmTiin分别为第i台机组的有功输出上限值和下限值。

2 FDCBBO算法

2.1 支配度的数值解法

2.1.1 模糊支配

假设最小化问题有Nobj个目标函数fi，其中，i=1，2，…，Nobj。

定义1 i维模糊支配。

定义一个非减的隶属度函数 μidom（fi（X）） [0，1]，i=1，2，…，Nobj。

若 fi（Xu）

定义2 解的模糊支配。

若∀iє｛1，2，…，Nobj｝，Xu≺FiXv，称解 Xu模糊支配解Xv，记作Xu≺FXv，模糊支配的程度可通过计算第i维模糊关系Xu≺FiXv（i=1，2，…，Nobj）的交集得出。 模糊交集可以通过一系列称为t-norms的函数求得，其操作用Ⅰ表示如下：

定义3 群体模糊支配。

考虑一个包含M个解的解集X。若X中的一个解Xv被X中剩余的任意一个解Xu支配，则称Xv在X内被模糊支配。这种情况下，模糊支配的程度可通过对每个可能的μdom（X≺FXv）求并集得出。模糊并集的求法由一系列被称为t-conorms的函数决定。具体方法参见文献[20]。

2.1.2 解的分布密度

某一解在解空间中的分布密度用每维目标函数上与其相邻2点的标准化距离之和表示，如式（9）所示：

其中，O（Xv）为 Xv处 Nobj维封闭超立方体的大小，此超立方体仅包含Xv1个解；Xu、Xw为将解集按第i维目标函数值fi（X）升序排列后与Xv相邻的解。边界解的O值赋为无穷。

由上述分析可知，解的分布密度越小，解集的多样性越好。

2.1.3 非支配度排序

对于待优化解集中的解，采取以下策略进行排序：

a.支配度小的在前；

b.对于支配度相同的解，分布密度小的在前。

采用以上策略处理多目标优化问题，将解集中的解按照优劣程度排序，可以促进帕累托最优前沿POF（Pareto Optimal Front）向理想帕累托曲线收敛及目标解集中的解在POF上的均匀分布。

2.2 BBO算法

BBO算法的参数包括栖息地的适宜度指数、栖息地的特征变量向量、优化问题中变量、某栖息地容纳的种群数量s及概率Ps、最大种群数量smax、迁入率λ、迁出率μ。系统变量包括系统迁移率Pmod和系统最大突变率mmax。算法中主要包括迁移和变异2种操作。

a.迁移。

BBO算法的迁移操作用于修正解集中已存在的解。首先根据Pmod判断是否对解集中的某个解K进行修正；然后使用λ决定是否对此解K中的第i个因子进行修正；最后使用μ从解集中剩余解中选出一个解u，用u的第i个因子代替K中原有的第i个因子。

b.变异。

变异操作用于增加群体的多样性。变异率由该栖息地种群数量概率决定：

其中，mmax为最大变异率，由用户决定；Pmax为栖息地种群数量达到最大时的效率。

2.3 FDCBBO算法

本文在基本BBO算法的基础上，用模糊支配求解解间的支配关系并将解集中的解排序，代替基本BBO算法中的栖息地适宜度指数作为解的评价标准，形成FDCBBO算法。在算法进化过程中，不再直接用迁移、变异后的个体代替原有个体，而是产生一个新的解集，与原解集融合，重新排序，选择2个解集中较好的个体形成下一代解集。FDCBBO算法流程如图1所示。

图1 基于模糊支配的生物地理学算法流程图Fig.1 Flowchart of proposed algorithm

3 算例分析

本文采用IEEE30节点系统验证所提FDCBBO算法的可行性及含风电场电力系统双目标优化模型的有效性。由于阀点效应对火电机组发电费用的影响很小，因此忽略不计。6台火电机组参数见表1和表2。系统负荷PD=2.834 p.u.，风电场运行费用系数δ=0.5元／MW，风电场在节点19接入系统，其有功出力Pw=20%PD。设置3种算法的种群规模及迭代次数均为50。GA采用单点杂交，杂交、变异率分别取1和0.01；PSO算法中惯性常量取0.3，学习因子均取1，邻域粒子数取7。

基于模糊支配的PSO算法、GA、BBO算法求解模型所得的POF分别如图2—4所示。POF两端极值点分别对应最优发电成本解和最优环境影响因子解。图2所示POF的形状与理想帕累托曲线相差很远，解在曲线上的分布极不均匀，两端分布稀疏，中部稍为密集。图3中的POF曲线中部较为光滑，但靠近最优发电成本端的曲线光滑程度较差，曲线的形状较接近理想帕累托曲线；解的分布同图2相比较均匀，但在POF极值点附近的分布仍不够理想。图4是基于本文所提出的FDCBBO算法所得POF曲线，从图中可以看出，该曲线光滑，形状与理想帕累托曲线最接近，且求得的非支配解在曲线上的分布均匀。

表1 发电机发电费用系数及有功容量Tab.1 Cost coefficients of power generation and active power capacities

表2 发电机环境影响因子系数Tab.2 Environmental influencing factor coefficients of generator

表3、表4列出了使用3种算法分别进行10次独立运算得到的最优发电成本解和最优环境影响因子解（表中PTi为标幺值）。通过比较可知，使用FDCBBO算法得到的最优发电成本解与使用FDCGA和FDCPSO算法所得的相应解相比，发电成本和环境影响因子均最小，因此更靠近原点。使用FDCBBO算法得到的最优环境影响因子解的环境影响因子虽然与使用FDCGA求得的相应值同为最小，但其发电成本仍为最小，因此更靠近原点。

综合以上分析可以得知，FDCBBO算法在收敛性和解的多样性方面均优于FDCGA和FDCPSO算法。

图2 基于模糊支配的粒子群优化算法所得的POFFig.2 POF derived by PSO with fuzzy dominance

图4 基于模糊支配的生物地理学算法所得的POFFig.4 POF derived by BBO with fuzzy dominance

表3 不同算法所得最优发电成本Tab.3 Optimal generation cost obtained by different algorithms

表4 不同算法所得最优环境影响因子Tab.4 Optimal environmental influencing factor obtained by different algorithms

在不同风电场有功出力的情况下，使用FDCBBO算法所得的POF曲线如图5所示。负荷一定时，随着风电场有功出力的增加，火电厂的总出力PTs减小。由图5可以看出，随着PTs的减小，发电成本减小的趋势较为明显，而环境影响因子则有缓慢的增加趋势，这是由于发电成本表达式和环境影响因子表达式均由火电机组有功出力的二次函数近似，函数值在最低点附近变化缓慢，远离最低点处变化快。虽然每台机组有独立的有功功率-发电成本特性曲线和有功功率-环境影响因子特性曲线，但是在火电总负荷波动达到一定值时，POF曲线会随火电机组运行特性曲线的总体变化趋势移动。由于火电机组的发电费用系数均为正，在功率的负半轴取到其发电费用特性曲线极小值点，所以在实际运行中火电发电总成本与火电总负荷大小成正比。同时，由于风电发电成本很小，系统发电成本近似与风电场等值出力大小成反比。 环境影响因子系数中，αi、γi为正值，而 βi为负值，在功率的正半轴取到环境影响因子极小值点，所以随着火电机组总出力增大，环境影响因子经历一个先递减再递增的过程。由于风电穿透极限功率有限，负荷一定时，火电机组的总出力变化不大，因此，风电的并网对电力生产环境效益影响十分有限。

随着PTs的变化，POF中发电成本和环境影响因子最大值的变化如表5所示。由于POF形状变化极小，发电成本和环境影响因子最大值的变化即可代表POF位置的变化。

图5 风电并网功率不同时的优化曲线Fig.5 Optimal curves for different grid-connected wind power

表5 发电成本和环境影响因子最大值随火电总负荷的变化Tab.5 Maximum of generation cost and environment influencing factor for different total thermal loads

综上所述，风电的加入对于减少发电成本有显著作用，而电力生产的环境效益则更多依赖于火电总负荷的大小、火电机组的环境影响因子特性曲线及负荷分配方案的选择。

4 结论

本文提出了应用BBO算法求解含风电场电力系统双目标优化调度问题的方法，并通过实例验证了算法的有效性，分析了不同风电场等值出力对含风电场电力系统电力生产经济效益和环保效益的影响，由此可得出如下几点结论。

a.在传统发电成本目标函数中加入风电发电成本，同时考虑污染物排放量作为环保目标，构建了含风电场的电力系统双目标优化调度模型。

b.将模糊支配与BBO算法结合，用于电力系统双目标优化调度问题的求解，实例验证表明，本文所提FDCBBO算法在解集收敛性及多样性方面均优于FDCGA和FDCPSO算法。

c.不考虑风电出力，当火电总出力由小增大时，系统电力生产的废气排量先减小后增大，环境效益先增加再降低。这说明电力生产环境效益的改善与火电总出力及环境效益因子特性曲线有关。

d.当系统内风电全部优先并网时，风电场等值出力的增加会显著降低发电成本，增加经济效益，但是对环境效益的改善则不明显；这也说明电力生产环境效益的改善更依赖于负荷分配方案的选择，同时，更突出了电力系统优化调度研究的重要性。

本文将FDCBBO算法用于双目标电力系统优化调度的求解，并未充分体现出模糊支配与其他支配度数值解法的优势。在本文的基础上，可以进一步改进优化模型，增加目标函数维数，更全面地考虑影响优化调度的诸多因素，体现FDCBBO算法的优越性。