基于混沌量子免疫算法的电力系统无功优化
2013-10-22童沛乐秀璠
童沛,乐秀璠
(河海大学能源与电气学院,江苏南京 210098)
电力系统无功优化是确保电力系统运行安全的有效手段之一。合理的无功分布可以提高电压稳定和减少系统损耗。传统的优化方法包括内点法、梯度法、非线性规划规[1-2]等,都各自具有一定的优越性和适应性,但会对目标函数要求可微,初值条件较高,且易陷于局部极值,求解时间较长,大规模的优化计算无法进行。由于无功优化特殊性,传统的这些优化方法显然不能满足电力系统发展需求。
近年来所提出的人工智能优化算法逐渐被引入到电力系统无功优化的研究中。这些方法投入到实际应用中已取得了良好的效果。文献[3]提出了自适应差分进化算法的无功优化。在该算法中,变异策略和3个控制参数都是依据经验进行自适应的,在约束条件下,电压波动达到良好的效果,系统有功网损与粒子群算法相比显著减少。文献[4]的改进微分进化算法提出了一种提高全局搜索效率的改进策略,在用于电力系统无功优化问题上具有准确、快速、高效的优点。
为了达到全局寻优,本文的混沌量子免疫算法[10](Chaos Quantum Immune Algorithm,CQIA)是融合混沌优化的遍历性、规律性和量子优化的种群多样性的优势,且使用混沌变量来初始化寻优量子抗体。在抗体克隆扩增和变异的过程中采用量子算法所特有的种群更新方式量子旋转门,由量子旋转门更新抗体上的量子相位。最后以IEEE30标准节点系统进行仿真计算,并与其他的优化方法比较结果,表明该算法的可行性和有效性。
1 无功优化数学模型
电力系统无功优化在状态变量不越限的条件下,通过对控制变量的改变来使系统的有功网损最小。控制变量包括无功补偿容量、可调变压器分接头、发电机的端电压;状态变量包括系统的节点电压和发电机的无功功率输出。
1.1 目标函数
系统的有功网损最小为目标函数定义下:
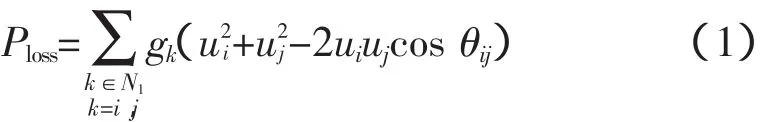
式中,Ploss为系统的有功网损;N1为支路数;gk为之路k的电导;ui为负荷节点i的电压幅值;θij为负荷节点i,j的电压相位差。
1.2 约束条件
等式约束条件为潮流方程:
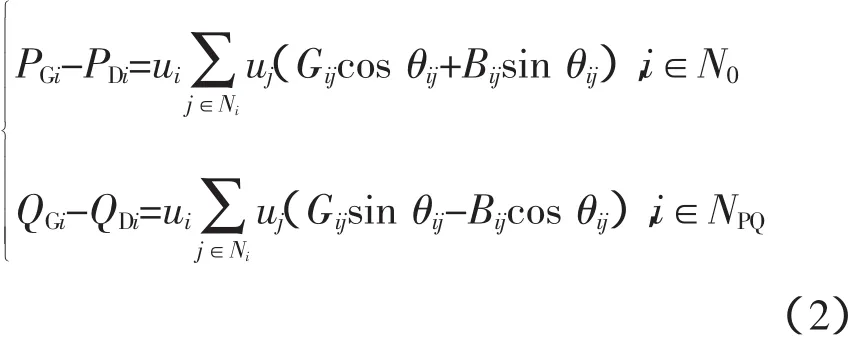
式中,N0是系统中母线总数的集合;Ni是直接与第i母线连接的母线集合;NPQ是PQ型母线集合;PGi、QGi是发电机的有功和无功出力;PDi、QDi是负荷的有功和无功;Gij、Bij是节点ij间的电导和电纳。
不等式约束包括控制变量和状态变量约束,控制变量约束为:
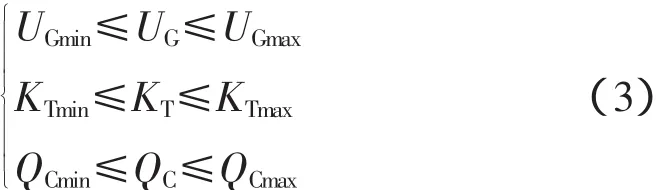
式中,UGmax、UGmin是发电机端电压的上下限;KTmax、KTmin是可调变压器变比的上下限;QCmax、QCmin是补偿电容无功容量上下限。
状态变量约束为:
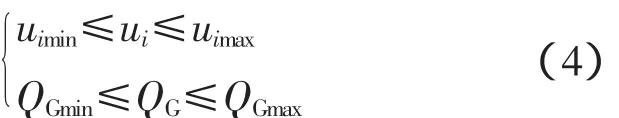
式中,uimax、uimin是节点电压的上下限;QGmax、QGmax是发电机的无功出力上下限。
将状态变量通过罚函数形式导入目标函数:
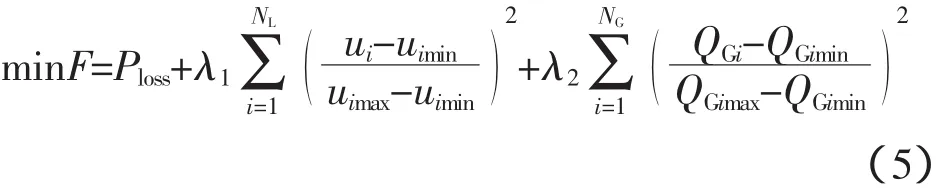
式中,λ1、λ2为惩罚系数;NL为系统节点总数;NG为发电机节点总数。
2 混沌量子免疫算法(CQIA)
2.1 混沌系统
混沌优化方法[5]是用混沌变量进行优化搜索的。由于混沌运动具有随机性、遍历性、规律性等特点,利用类似载波方法将混沌运动的遍历范围扩大到寻优变量的取值范围,然后使用混沌变量来寻优,保证寻优的全局性。产生混沌变量模型为Logistic映射即:

当μ=4时系统为混沌状态,混沌变量的取值范围在[0,1],但不能是0.25、0.50、0.75。在实际寻优问题中需要用式(7)将混沌变量的空间映射到寻优变量的解空间上。

式中,Xn为寻优变量的解,Xn∈[a,b]。
2.2 免疫优化算法
免疫优化算法[7]是基于人体免疫机制,采用克隆选择算子的算法。在算法中,抗原对应于需要解决的问题,抗体是问题的解。寻优的依据是抗体的亲和力,在实际问题对应的是目标函数。亲和力高的抗体通过克隆裂变,产生新的抗体,保证了搜索效率。亲和力低的抗体通过变异操作,提高了全局搜索能力。
2.3 量子进化
量子进化算法[9]的最小单元是量子位,一个量子位的状态可以表示为:

α,β为量子概率幅,满足α2+β2=1。由式(8)可知一个量子态可以是0态、1态,也可以是任意叠加态。一个种群第n个个体有m个量子位则可以定义为:
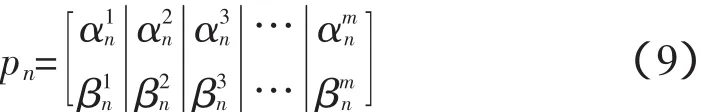
2.4 混沌量子免疫算法
设含有m个变量的函数优化问题可表示为max f(X1,X2,…,Xm)(最小值问题可以变换)优化变量,Xi∈[ai,bi](1≤i≤m)。在使用CQIA优化计算时,抗体对应于求解问题的解,抗体亲和力由目标函数计算到。
初始优化抗体生成,给定m个初始值,用式(6)产生m个混沌变量xi1(1≤i≤m),利用这m个混沌变量初始化种群第一个抗体。然后依次令n=1,2,…,N-1产生另外的N-1个抗体。第n个抗体则如式(10):
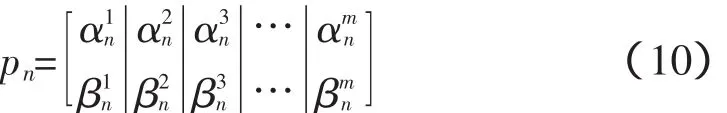
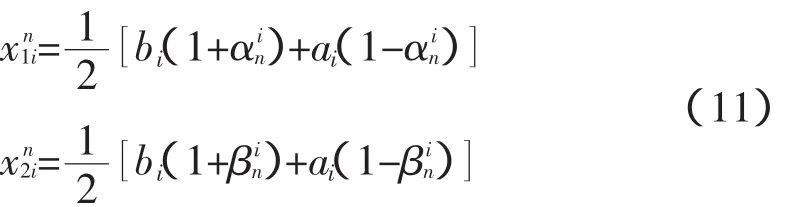

此时Δθki∈ k-λk,λkk,设第k个克隆母体为:
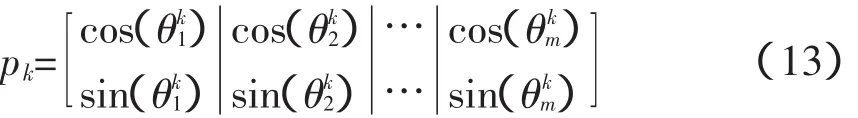
使用量子旋转门后抗体为:
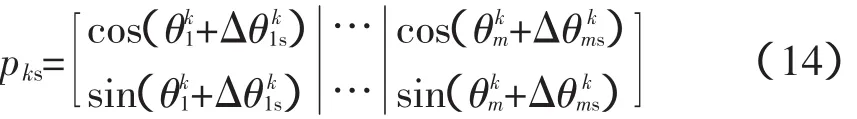
转角方向不需要与当前最优抗体进行比较,有利于提高种群多样性和搜索效率。对于克隆扩增后的抗体中亲和力低的抗体使用变异手段,通过施加混沌扰动来改变量子位的相位。设亲和力最低的r个抗体按照升序排列,则第k个母体变异相角幅值为:
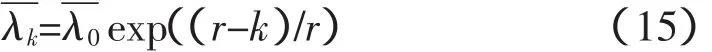
3 CQIA算法在无功优化中应用
将CQIA算法用于电力系统无功优化中,具体步骤如下:
1)根据系统确定节点信息、支路信息、控制变量个数及各变量的取值范围。由控制变量的初始值和式(10)产生第一代寻优量子抗体p1,p2,…,pN。
2)将目标函数F最小值问题转换为最大值问题Ffitness=C/F,其中C为适当的常数。调用软件包对量子抗体潮流计算得出各抗体的亲和力,潮流计算时需要将量子抗体概率幅由单位空间映射到控制变量解空间。
3)在保证种群规模稳定的条件下,依据亲和力的高低进行克隆扩增和变异操作。操作完成后替换上一代亲和力低的抗体形成新一代母体,判断是否满足终止条件,若满足则转步骤4),不满足则转步骤2)。
4)寻找亲和力最高的抗体由式(11)输出结果。
具体算法流程见图1。
4 算例分析
本文以IEEE-30节点系统进行仿真计算,该系统发电机节点有6个,分别为1、2、5、8、11、13,其中节点1为平衡节点,其余为PV节点,剩下的为PQ节点,4个变压器支路(6-9、6-10、4-12、27-28),3个并联电容器节点(3、10、24),标幺值的基准功率为100 MV·A,PV节点电压范围是[0.9,1.1],PQ节点电压范围是 !0. 9 5,1.05",变压器变比范围是 !0. 9 5,1.05",并联电容器无功出力范围是 !-0 . 12,0.36"。算法中的参数设置见表1。
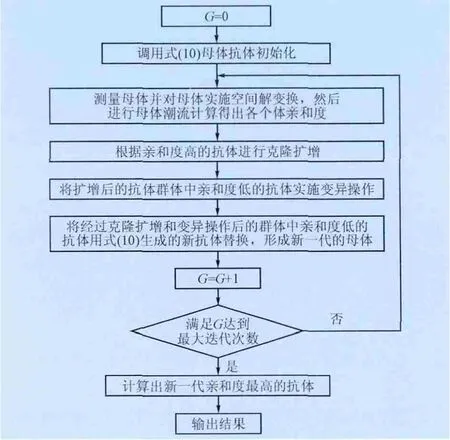
图1 CQIA算法流程图Fig.1 Flow chart of the CQIA algorithm
系统总负荷Pload=2.834,Qload=1.262。初始条件下设置变压器变比和发电机节点电压都为1.0。潮流计算得到∑PG=2.893 86、∑QG=0.980 2、Ploss=0.059 86。3处PQ节点发生了越限,V26=0.933、V29=0.941、V30=0.927。为了验证CQIA算法的正确性和有效性,分别与改进免疫算法[11](IIA)、改进量子遗传算法[12-13](IQGA)进行比较。表2给出了以上3种方法对系统进行30次仿真。
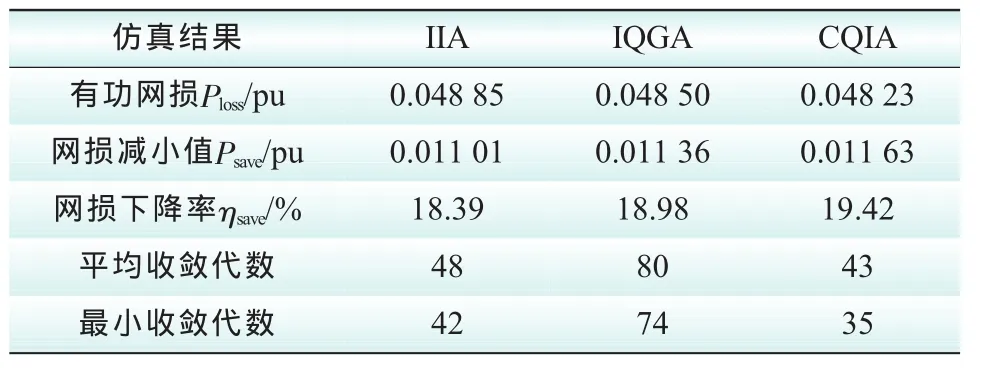
表2 仿真结果统计Tab.2 Statistics of results by three algorithms

表1 参数设置Tab.1 Simulation parameters
由表2统计结果可以看出,所用的CQIA算法优化后的系统有功网损比另外2种算法的有功网损得到了减少。IIA和IQGA的有功网损分别为0.048 85和0.048 50,而CQIA的有功网损为0.048 23,网损下降率较前2种算法明显增大。在收敛速度上看,CQIA在平均43次迭代时收敛到稳定值,而IIA和IQGA平均收敛代数分别为48和80,收敛速度要慢于CQIA,因此CQIA的收敛性比另外2种方法要好。
图2是3种算法仿真过程中同代最优个体平均有功网损曲线。从曲线的收敛速度和收敛值可知CQIA算法不仅在收敛速度上表现较快,而且在系统有功网损上也能够很好地减少,说明该算法适合电力系统无功优化。
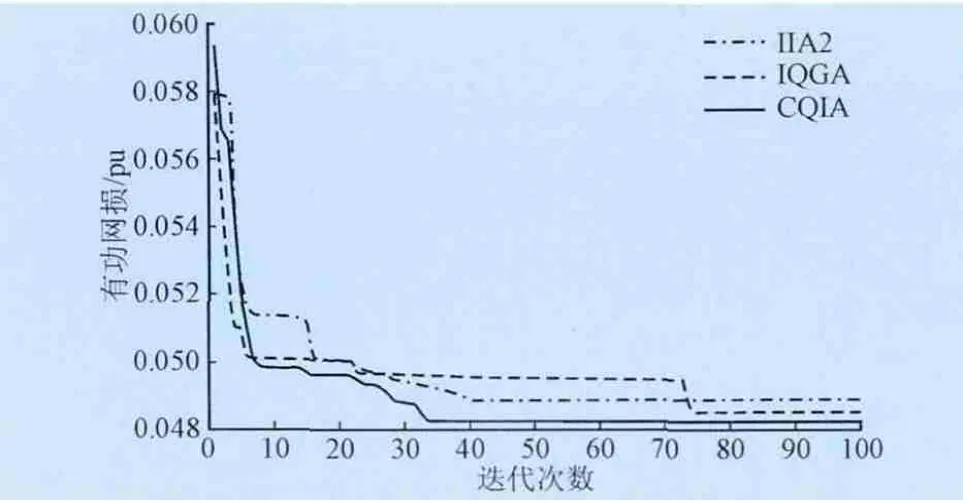
图2 IEEE-30节点系统平均网损收敛曲线Fig.2 The convergence curves of average active power loss for the IEEE-30 bus system
图3 是3种算法优化系统节点电压平均幅值曲线,由图3可知经CQIA算法优化后节点电压均在幅值范围内,均没有发生越限。曲线的平稳度较IIA和IQGA算法后更好,所用的算法用于无功优化后,系统的节点电压均保持良好的水平。
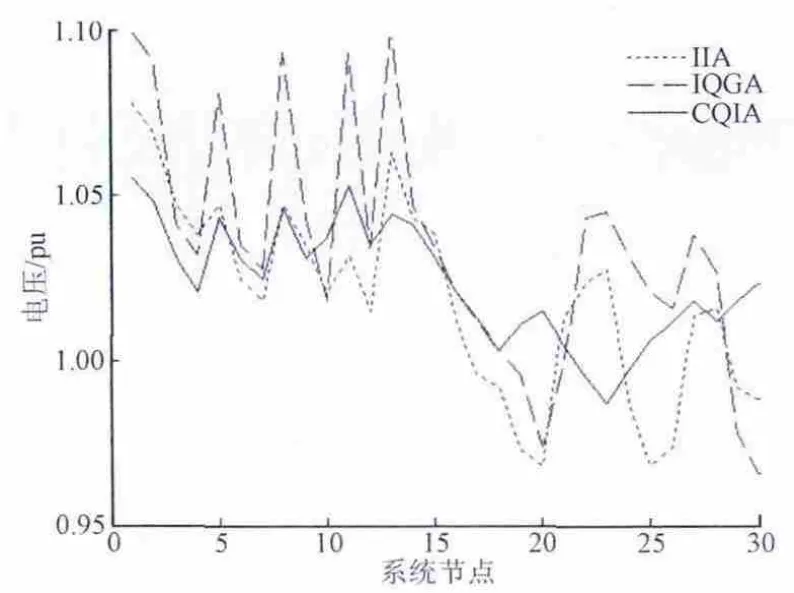
图3 IEEE-30节点系统平均电压幅值曲线Fig.3 The average voltage magnitude curves for the IEEE-30 bus system
5 结论
本文所用的混沌量子免疫算法综合考虑了免疫优化和混沌优化各自在空间搜索的优势以及量子优化的快速高效性。在进化过程中采用量子优化,保持了种群多样性,引入的混沌变量搜索策略,保证算法的全局搜索能力进一步提高。由仿真结果可知CQIA算法收敛速度快,全局寻优能力突出,同时可以维持系统电压处在一个良好范围内,能够有效地用于电力系统无功优化。
[1]MOMOH JA,EL-HAWARY M E,ADAPA R.A review of selected optimal power flowliteratureto 1993.I.Nonlinear and quadratic programming approaches[J].IEEE Transactions on Power Systems,1999,14(1):96-104.
[2] 刘明波,李健,吴捷.求解无功优化的非线性同伦内点法[J].中国电机工程学报,2002,22(9):1-7.LIU Ming-bo,LI Jian,WU Jie.Nonliner homogeneous interior point method for reactive power optimization[J].Proceedings of the CSEE,2002,22(9):1-7(in Chinese).
[3] 赵树本,张伏生,钟继友,等.自适应差分进化算法在电力系统无功优化中应用[J].电网技术,2010,34(6):169-174.ZHAO Shu-ben,ZHANG Fu-sheng,ZHONG Ji-you,et al.An adaptive differential evolution algorithm and its application in reactive power optimization of power system[J].Power Systerm Technology,2010,34(6):169-174(in Chinese).
[4] 刘自发,闫景信.基于改进微分进化算法的电力系统无功优化[J].电网技术,2007,31(18):68-72.LIU Zi-fa,YAN Jing-xin.Power system reactive power optimization based on improved differential evolution algorithm[J].Power Systerm Technology,2007,31(18):68-72(in Chinese).
[5] 赵涛,熊信银,吴耀武.基于混沌优化算法的电力系统无功优化[J].继电器,2003,31(3):20-22.ZHAOTao,XIONGXin-yin,WUYao-wu.Reactive power optimization of power systerm based on chaos optimization algorithm[J].Relay,2003,31(3):20-22(in Chinese).
[6]AZZAM M,MOUSA A A.Using genetic algorithm and TOPSIS technique for multiobjective reactive power compensation[J].Electric Power Systems Research,2010,80(6):675-681.
[7] 王磊,潘进,焦李成.免疫算法[J].电子学报,2000,28(7):74-78.WANG Lei, PAN Jin, JIAO Li-cheng.The immune algorithm[J].Acta Electronica Sinica,2000,28(7):74-78(in Chinese).
[8]ALRASHIDI M R,EI-HAWARY M E.Applications of compu-tation intelligence techniques for solving the revived optimal power flow problem[J].Electric Power System,2009,79(4):694-702.
[9]娄素华,吴耀武.量子进化算法在电力系统无功优化中的应用[J].继电器,2005,33(18):30-35.LOUSu-hua,WUYao-wu.Application of quantuminspired evolutionary algorithm[J].Relay,2005,33(18):30-35(in Chinese).
[10]李盼池,李士勇.求解连续空间优化问题的混沌量子免疫算法[J].模式识别与人工智能,2007,20(5):654-660.LI Pan-chi, LI Shi-yong.A chaos quantum immune algorithm for continuous space optimization[J].PR&AI,2007,20(5):654-660(in Chinese).
[11]郭创新,曹一家.基于改进免疫算法的电力系统无功优化[J].电力系统自动化,2005,29(15):23-29.GUO Chuang-xin,CAO Yi-jia,et al.Power system reactive power optimization based on an improved immune algorithm[J].Automation of Electiic Power Systems,2005,29(15):23-29(in Chinese).
[12]刘红文,张葛祥.基于改进量子遗传算法的电力系统无功优化[J].电网技术,2008,32(12):35-39.LIU Hong-wen,ZHANG Ge-xiang.A reactive power optimization method based on improved quantum inspired genetic algorithm[J].Power System Technology,2008,32(12):35-59(in Chinese).
[13]姚李孝,肖靓,王磊,等.基于改进遗传算法的配电网无功优化[J].电网与清洁能源,2009,25(4):24-28.YAO Li-xiao,XIAO liang,WANG Lei,et al.Reactive power optimization based on improved genetic algorithms in distribution system[J].Power System and Clean Energy,2009,25(4):24-28.
