黄茨滑坡时间预报反分析

李先福，魏雨溪，杨红梅

（1.武汉工程大学环境与城市建设学院，湖北 武汉 430074；2.中国五环工程有限公司，湖北 武汉 430223）

0 引 言

我国是一个多山的国家，特殊的地质条件导致滑坡等地质灾害频发，且人员财产损失严重.据初步统计，我国每年因为滑坡导致的直接经济损失达200多亿元，代价巨大.滑坡预报分为空间预报（区域性滑坡预报、单个滑坡预报等）、时间预报、滑坡灾害范围预报等［1］.其中时间预报因其具有预报困难，且在保护人员财产免受损失方面的重要作用等特点，对此进行研究具有实用意义.

据许强［2］等研究，滑坡时间预报可以分为确定性预报模型、统计预报模型和非线性预报模型.滑坡具有模糊性、灰色不确定性等特点，灰色模型较适用于滑坡时间预报［3－4］.Verhulst模型是非线性预报模型的一种，德国生物学家Verhulst在1987年研究生物的繁殖规律时发现的.该灰色模型可以较好地模拟生物种群的繁衍、生长、成熟和消亡的过程，在预报系统的未来运行状态方面具有明显优势，已广泛运用于交通、工业、农业、经济等领域.晏同珍［5－7］教授认为滑坡也有一个变形、破坏、发展和破坏的过程，二者具有一定的相似性，于是把这一灰色模型引进到滑坡位移时间预报中.

铁道科学研究院西北分院于黄茨滑坡（1995，甘肃）剧烈滑坡前成功预报该滑坡，成为我国滑坡时间预报方面成功的典型案例，并积累了宝贵的监测数据.本研究采用Verhulst灰色模型，结合黄茨滑坡位移监测信息，对该滑坡临滑时间预报进行反分析，并和实际监测值进行对比分析，以验证灰色Verhulst模型应用于滑坡时间预报中的适用性.

1 Verhulst预报模型基本原理

本文采用基于位移信息的Verhulst灰色模型.早在1988年该模型就由晏同珍应用于滑坡的时间预报研究中，1996年殷坤龙、晏同珍等进一步发展完善［8－9］.其微分方程形式如下：

其中，a，b是系数，用灰色系统模型求解.其解为

系数a，b的灰色求解：

滑坡位移监测数据（等时间距 Δt）：x（0）1，x（0）2，…，x（0）n

累加生成操作（AGO）生成数列：x（1）1，x（1）2，…，x（1）n （x（1）k＝x（0）1＋x（0）2＋…＋x（0）k）

根据原始观测数据及累加时辰数列建立矩阵A、B、YN：

a、b系数据式（3）求解：

2 黄茨滑坡概况

黄茨滑坡位于兰州以西60km处的黄河左岸，黄河四级阶地构成的台地的南缘，滑坡前缘直抵黄茨村，直接威胁黄茨村63户居民的生命财产安全.

黄茨滑坡是一个老滑坡，经历过多次滑动.由于多年农业灌溉而产生的沉降裂缝已出现十数年，后演化为滑坡后缘裂缝.西侧顺层面的滑面也已显现数年之久.1994年，前缘剪出裂缝、鼓胀裂缝等陆续出现［8］.

1997年1月27日，铁道科学研究院西北分院根据半年来的调查、监测，分析计算后认为该滑坡会于1月31日至2月7日发生整体滑动，并发出预警报告.后该坡于1月30日凌晨发生滑动.

3 黄茨滑坡时间预报反分析

滑坡体上不同部位的变形和破坏发展情况不同，时间预报应尽量选择不同部分的位移监测数据进行综合分析.根据当时所收集的资料，电子单点位移计A7、B2均位于滑坡后缘，且A7的监测线跨越了后缘裂缝，所记录的数据可以充分说明滑坡当时的变形破坏情况.这里用A7、B2所采集的日位移量数据进行滑坡临滑时间预报.位移监测起始时间为1995年1月23日至1995年1月29日，如表1.

表1 黄茨滑坡位移监测表Table 1 Displacement monitoring table of Huangci landslide

用Matlab编制相应的程序，经过计算后可得到a、b值，从而得到滑坡时间的预测值.据A7位移信息，预计滑坡发生时间为1月28日16时.据B2位移信息，预计滑坡发生时间为2月3日7时.滑坡实际发生时间为1月30日3时，预测值与实际值虽有一定程度的误差，但基本吻合.

以B2位移监测点为例，根据计算得到的a、b值（a＝0.4432，b＝0.0001）和V氏模型的微分方程，可分别计算得到B2监测点在未来各时间点的位移值，从而得到B2监测点位移时间预报曲线.据曲线可以推测得出滑坡体在未来一段时间的变形发展趋势，以供预报工作参考.结果如图1所示.

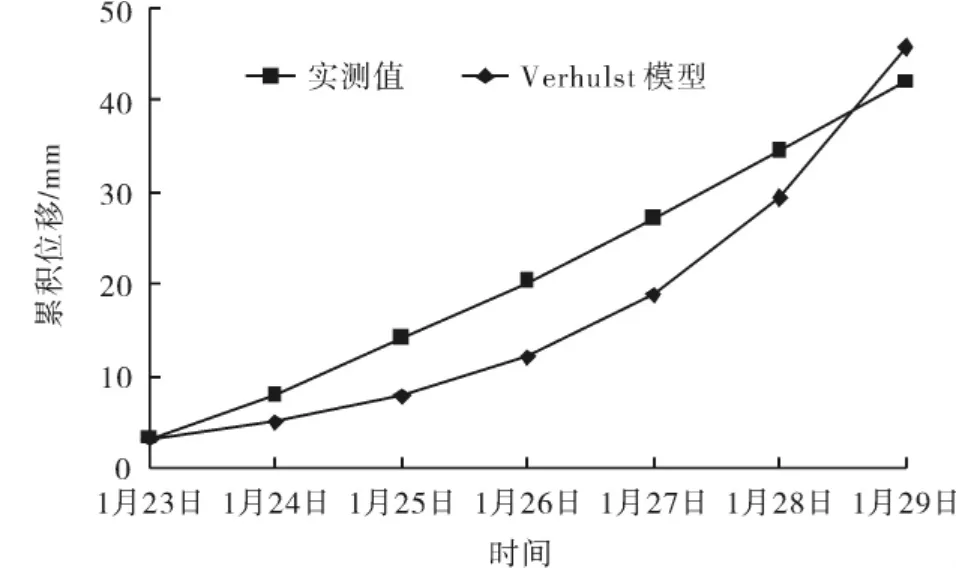
图1 B2监测点位移时间预报曲线Fig.1 Prediction curve of the displacement time in B2monitoring point

由图1知，据Verhulst模型得到的位移预报曲线，滑坡从1995－01－28已经进入明显加速蠕变阶段.Verhulst模型的累积位移时间预报与实测结果拟合较好.由图1的Verhulst位移时间预报曲线可以看出，位移进入加速上升阶段，预示大规模滑坡即将发生.

灰色Verhulst模型要求原始监测数据具有非负、等时距、单调等特征，当原始数据波动较大时，模型的精度较低，可以考虑用一定的数学方法处理原始数据，减少其波动性.

实际监测预报工作中，也不能仅凭一个点的预报结果就做出结论.如果增加样本量，并采用一定的数学办法如插值处理原始数据，剔除病态数据，预计预报精度会有进一步的提高.此外，合理的位移监测点布置、合适的记录时间间隔、位移数据的数学处理及多个监测点位移数据的综合分析有助于提高预报精度.

实际滑坡的发生是一个复杂的地质过程，受地层条件、水文条件、气候特征及人类活动等因素的影响，各滑坡的主要因素及变形机理也不尽相同.因此滑坡时间预报模型的选用需要根据实际情况选用，不可千篇一律地采用同一个预报模型进行预报.这里采用Verhulst灰色模型对黄茨滑坡时间预报的反分析虽然与实际监测结果存在一定的出入，但整体上看，灰色Verhulst模型应用于滑坡时间预报是可行的.

4 结 语

通过对黄茨滑坡的临滑时间预报反分析所作出的结论，得出了灰色Verhulst模型应用于滑坡时间预报的几点结论和建议：

a.滑坡和生物体具有类似生长、生熟、消亡的过程，灰色Verhulst模型应用于黄茨滑坡时间预报，经检验是可行的.

b.经过反分析计算，黄茨滑坡时间预报结果与滑坡的实际滑动时间基本吻合，预测滑坡变形曲线基本与位移监测值展布趋势一致.

c.合理的位移监测点布置、合适的记录时间间隔、位移数据的数学处理及多个监测点位移数据的综合分析有助于提高预报精度.

［1］徐峻龄，廖小平，李荷生.黄茨大型滑坡的预报及其理论和方法［J］.铁道工程学报，1996，7（2）：197－205.

［2］许强，黄润秋，李秀珍.滑坡时间预测预报研究进展［J］.地球科学进展，2004，19（3）：478－483.

［3］肖云，李先福.基于优化的灰色GM模型的滑坡预测［J］.武汉工程大学学报，2012，34（1）：31－35.

［4］温文，吴旭彬.Verhulst模型在黄茨滑坡临滑预报中的应用［J］.人民珠江，2005（5）：39－40.

［5］殷坤龙，晏同珍.滑坡预测及相关模型［J］.岩石力学与工程学报，1996，15（1）：1－8.

［6］崔立志，刘思峰，李致平.灰色离散Verhulst模型［J］.系统工程与电子技术，2011，33（3）：590－593.

［7］程江涛，刘莉.基于Verhulst模型的滑坡位移预测研究及其程序化实现［J］.岩土工程技术.2008，23（5）：217－222.

［8］毛广湘.黄茨滑坡预测预报分析［J］.建筑科学，2007，23（3）：31－33，37.

［9］周柏成，王磊，杨辉建.两种数学模型在黄茨滑坡预报中的应用研究［J］.科技资讯，2007（18）：1－3.