改进型模糊自整定比例积分微分温度控制系统

李 平，王 欣

（武汉工程大学邮电与信息工程学院，湖北 武汉 430074）

0 引 言

真空冶金技术在现代冶金技术中扮演了重要的角色，而温度控制又是真空冶金技术的重要的一环.通常，真空冶金工程中的温度控制采用的是比例积分微分（Proportional Integral Differential，以下简称：PID）控制系统，但是传统PID控制存在超调量大、调节时间长等问题［1］.为了解决上述问题，传统PID控制、模糊控制、人工智能控制、模糊自整定PID控制等方法被应用到温度控制中［2］.由于模糊自整定PID控制算法容易实现，所以该算法被广泛用在温度控制系统中［3］.所以提出一种改进型的模糊自整定PID控制算法对电炉温度进行控制，该算法在传统的PID控制器算法上，计算系统误差及其变化，再根据模糊推理等相关知识来实现控制过程.

1 电炉温度控制系统

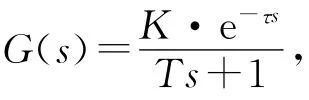
传统PID控制的传递函数模型为：G（s）＝KP（1＋＋Tds），式中KP是比例增益，τ是惯性时间常数，Ti是积分滞后时间常数，Td是积分滞后时间常数，s是传递函数的变量.电炉温度控制系统的模型如图1所示.

图1 传统PID温度控制系统Fig.1 Temperature control system on the conventional PID

2 模糊自整定PID控制器设计

2.1 模糊自整定PID控制器

在传统的PID控制器的基础上，利用模糊推理的原理和变论域的在线PID参数调整知识［5］，对电炉系统进行控制.变论域是指输入域为Ei＝［－Ei，Ei］可以随系统误差ei变化而变化，输出域U＝［－U，U］可以随着控制输出u的变化而自动变化.数学表达式如下：

α（ei）是论域Ei的伸缩因子，β（u）是论域U 的伸缩因子.模糊控制器的调节能力可以通过变论域的α（ei）和β（u）伸缩因子实现.模糊自整定PID控制器的结构图如图2所示.

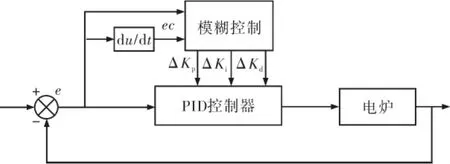
图2 模糊自整定PID控制器Fig.2 Fuzzy self－tuning PID controller

在控制系统中，e是系统误差，ec是系统误差的变化速率，两者作为系统输入参数；ΔKp，ΔKi，ΔKd分别是控制器的比例、积分、微分参数的输出变量.在PID算法的基础上，先计算出误差e和误差变化ec，然后依据模糊子集的隶属关系、参数的控制模型和在线PID参数调整计算出ΔKp，ΔKi，ΔKd.

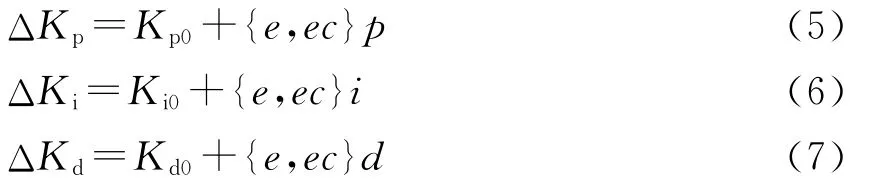
Kp0是控制器的比例参数的初始值；Ki0是控制器的积分参数的初始值、Kd0是控制器的微分参数的初始值.模糊（e，ec，ΔKp，ΔKi，ΔKd）＝（NB，NM，NS，ZO，PS，PM，PB），其中（NB，NM，NS，ZO，PS，PM，PB）表示（负大，负中，负小，零，正小，正中，正大）.根据电炉温度变化特点，ΔKp，ΔKi，ΔKd域分别为｛－3，－2，－1，0，1，2，3｝.

2.2 模糊自整定PID控制规则设计

ΔKp，ΔKi，ΔKd的自整定在不同误差和误差变化情况下有不同的要求：当误差e大时，要求ΔKp较大，ΔKd较小；当误差e和误差变化ec中等时，要求ΔKp，ΔKd适中，ΔKi较小；当误差e较小时，要求ΔKd，ΔKi变大，而误差变化ec较小时，ΔKd应增大.误差变化ec较大时，ΔKd应减小［5］.根据传统PID调节规律和电炉温度变化规律，自整定模糊控制参数ΔKp，ΔKi，ΔKd的规则如表1所示.

根据表1中ΔKp，ΔKi，ΔKd的控制规则，进行参数矫正，公式如下：

式（8）中：Kp0是控制器的比例参数的初始值；Ki0是控制器的积分参数的初始值、Kd0是控制器的微分参数的初始值，一般是现场调试得到的结果.ΔKp，ΔKi，ΔKd是控制器的输出值，Kp、Ki、Kd是调整后的PID实际控量.

表1 ΔKp，ΔKi，ΔKd 控制规则Table 1 Fuzzy Rule forΔKp，ΔKi，ΔKd

3 仿真结果与分析

在Matlab中建立自整定PID控制的电炉仿真结构图，如图3所示.

系统仿真时，PID传递函数中参数分别设置为 K＝80，T＝150s，τ＝20，初始值为 Kp0＝0.017，Ki0＝0.0087，Kd0＝0.001.根据系统中变量响应参数的规则和反复的模拟结果表明，当e＝0.0033，ec＝0.5，Kp＝0.001，Ki＝0.003，Kd＝0.001时PID控制的效果较好.

本文电炉主要用于轻质耐火粘土的生产，所以其参考温度分别设为500℃、1000℃，模拟时间为2000s，响应的结果如图4所示.

图3 模糊自整定PID控制仿真模型Fig.3 Fuzzy self－tuning PID of simulation model

图4 参考温度为500℃，1000℃时两种控制器响应曲线Fig.4 Response curve of the two controllers when reference temperature is 500℃，1000℃

从图4中可以发现，模糊自整定PID控制比传统PID控制的动态响应曲线要好.当控制的温度为500℃时，常规PID控制算法的超调量大约为8%，其调节时间大约在1000s；本文算法的超调量大约为1%，其调节时间大约在600s.当控制的温度为1000℃时，常规PID控制算法的超调量大约为9%，其调节时间大约在1400s；本文算法的超调量为1.1%，其调节时间大约在1100s.本文算法明显超调量减小，响应的速度快，性能有较好的改善.

4 结 语

本文采用改进型的模糊自整定PID控制算法发挥了传统PID控制和模糊控制的优点，能够根据误差e和误差变化率ec对PID的参数进行在线控制修正.在仿真实验中对500℃的炉温控制较为理想，而在1000℃的炉温控制时有一些波动，经分析，是由于在仿真实验时，电炉体积设计较小，加入的干扰温度过高所致，所以在现实生产过程中对电炉温度控制时，本文的算法是有一定的参考价值的.

［1］李卓，萧德云，何世忠.基于Fuzzy推理的自调整PID控制器［J］.控制理论与应用，1997，14（2）：238－242.

［2］刘闯.自整定模糊控制器的设计与优化［D］.辽宁：大连理工大学，2008.

［3］岳建锋.FUZZY－PI控制器在水温控制系统中的应用［J］.天津工业大学学报，2006，25（2）：65－67.

［4］汪新星，张明.利用改进微粒群算法优化PID参数［J］.自动化仪表，2004，25（2）：19－22.

［5］相征，郎郎.基于Fuzzy－PID控制器的网络化智能温度控制系统［J］.工业控制计算机，2008，21（3）：54－57.