含水率对花岗岩残积土邓肯－张模型参数影响

吴能森，赖榕洲，邹文平，林智雄，徐 青

（福建农林大学交通与土木工程学院，福建 福州 350002）

0 引 言

花岗岩残积土是花岗岩经风化后残留在原地的碎屑物，具有很强的结构性，在原位状态或土的微结构未受损伤时呈现高强度、中低压缩性［1］.但花岗岩残积土经过浸水饱和后，承载力降低，压缩性增大，在具有临空面的浸水条件下，花岗岩残积土会因软化崩解而坍塌［2］.事实上，含水率对所有岩土的力学性质都有很大影响，因此也是研究热点之一，如李险峰［3］通过三轴排水剪切试验，研究了含水率对滑坡碎屑土力学特性的影响.土的本构模型是研究岩土力学性质的核心问题，显然，研究含水率对花岗岩残积土本构模型参数的影响具有理论与工程实际意义.近几十年来，国内外学者提出描述土体应力－应变关系的本构模型多达数百个，这些模型基本上可分为弹性、弹塑性及其他各种新型模型.邓肯－张模型因其概念清晰，模型参数明确易得，自提出后40多年来得到了不断完善，被广泛应用于工程实践中［4］.

本研究进行了一系列不同含水率条件下花岗岩残积土的固结排水三轴试验，分析不同围压下花岗岩残积土的应力－应变曲线特点，通过计算得到不同含水率花岗岩残积土的邓肯－张模型参数，分析并归纳含水率对花岗岩残积土邓肯－张模型参数影响的基本规律.

1 模型简介

1963年，康纳（Kondner）［5］在大量三轴试验基础上，提出围压为常数的常规三轴固结试验的加工硬化型应力－应变关系可近似地用双曲线来表示，即：

式（1）中，a、b为试验常数，ε1为轴向应变，σ3为围压，σ1为轴向主应力.

可将式（1）改写为：

式（2）是一直线方程，a、b分别为该直线的截距、斜率，可通过试验数据拟合直线获得.

1970年，邓肯（Duncan）和张（Chang）等［6］根据式（1）提出了包括切线模量Et和切线泊松比μt的邓肯－张本构方程式，简称邓肯－张模型E－μ模型.其中切线模量Et表达式为：

式（3）（4）中：Ei为初始切线模量（kPa），c为土的粘聚力（kPa），φ为土的内摩擦角（°），Rf为破坏应力比，K、n为试验常数，Pa为大气压力（取101.4kPa）.

Ei、Rf与a、b的关系为：

式（5）（6）中，（σ1－σ3）f为土样破坏时的偏应力.

将式（4）进行坐标变换，可变为lgEi～lgσ3直线，则该直线斜率为n，当lgσ3＝1时的lgEi值即为lgK.

2 试验研究

2.1 试验土样

试验土样取自福州晋安区鹤林新城二区某地块，取土深度为12.3～16.8m，土样呈褐黄、肉红色，湿－稍湿，硬塑状态，土样的物理性质指标如下：天然密度ρ＝1.84g／cm3，天然含水率ω＝30.1%，土粒相对密度ds＝2.72，天然孔隙比e＝0.976，液限ωL＝41.1%，塑限ωP＝27.3%，塑性指数Ip＝13.8.经筛分，土样各粒组的分布情况见表1.土样击实试验的最优含水率ωop＝17.4%.

表1 花岗岩残积土粒组分布情况Table 1 Granularity distribution of the granite residual soil

2.2 试验方案

试验仪器为SLB－1型应力－应变控制式三轴剪切渗透试验仪，采用固结排水三轴压缩试验（CD试验）［7］，花岗岩残积土经过风干、碾碎、过孔径为2mm筛后，测定风干后土样的含水率，然后按照设计的含水率制作试样，试样按击实法制备扰动土制样方法制作，试样直径39.1mm，高80 mm.试样含水率以最优含水率为基准，上下相差4%左右，经取整分别为13%，17%，21%.试验固结围压σ3分别取100、200、300kPa，当体积读数变化微小或长时间保持不变时认为试样完成固结.固结完成后，在围压σ3保持不变的情况下，采用应变控制方式，以0.012%／min剪切速率增加轴向压力进行排水剪切，直至试样轴向应变值达到15%时停止试验，试验过程中排水阀始终保持开启状态.自动数据采集系统能够在试验过程中采集试验数据并绘制相关曲线.

2.3 试验结果及分析

2.3.1 试样变形特征及应力－应变特性 各含水率试样在三种不同围压下，均在轴向应变达到15%时呈比较明显的鼓状变形，但尚未发生剪切破坏.各试样的变形情况见图1.图2为各含水率试样的主应力差（σ1－σ3）与轴向应变ε1关系曲线，可见，不同含水率花岗岩残积土试样在固结排水条件下得到的应力－应变曲线形状相似，未出现明显的峰值，均呈非线性的加工硬化型曲线，与邓肯－张模型的条件式（1）基本吻合.

2.3.2 邓肯－张模型参数及分析 根据三种围压σ3作用下试样破坏时的偏应力（σ1－σ3）f试验数据，可绘制出不同含水率下三组试样的强度包线，见图3，得到不同含水率的花岗岩残积土抗剪强度指标c、φ值.

图1 试样破坏时变形特征Fig.1 Deformation of destroyed test samples

图2 （σ1－σ3）－ε1 关系曲线Fig.2 The curves of（σ1－σ3）－ε1

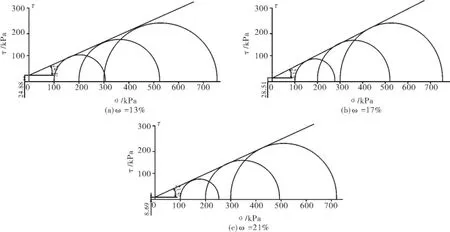
图3 三轴剪切摩尔强度包线Fig.3 The Mohr stress circles of triaxial compression test

将（σ1－σ3）－ε1试验数据按式（2）处理并绘制直线，可得试验常数a、b，进而根据式（5）、（6）得到初始切线模量Ei和破坏应力比Rf.再利用式（4）的线性化变换和绘图，得到试验常数K、n.

以上6个邓肯－张模型参数及主要试验数据见表2.依表2绘制得到各参数随含水率的变化情况，见图4～图8.

表2 不同含水率花岗岩残积土邓肯－张模型参数表Table 2 Parameters of Duncan－Chang model under different water content

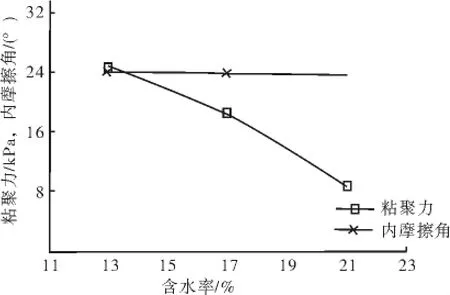
图4 粘聚力c与内摩擦角φ随含水率变化Fig.4 Cohesion c and internal friction angleφ change with the water content

图5 初始切线模量Ei随含水率变化Fig.5 Initial tangent modulus Ei changes with the water content

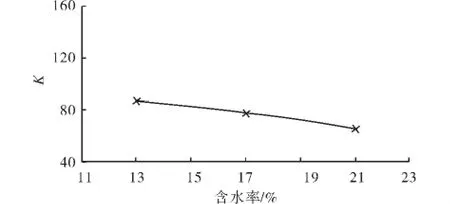
图6 参数K随含水率变化Fig.6 Parameter Kchanges with the water content

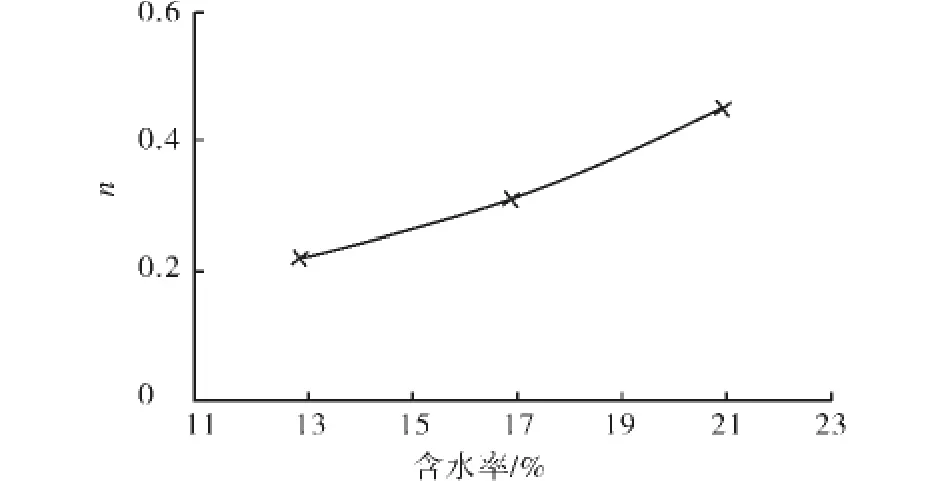
图7 参数n随含水率变化Fig.7 Parameter nchanges with the water content

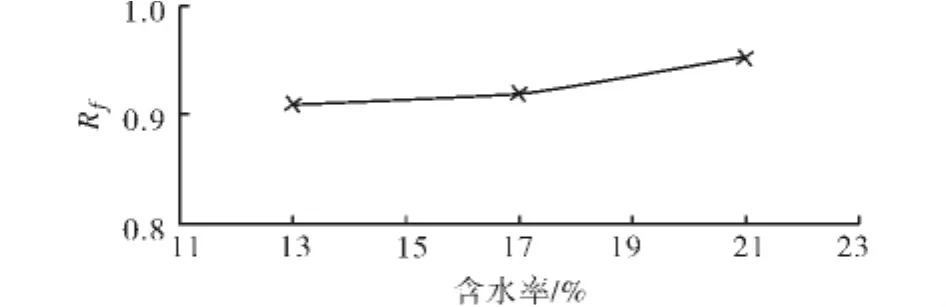
图8 参数Rf随含水率变化Fig.8 Parameter Rfchanges with the water content

由图4可见，含水率对花岗岩残积土抗剪强度指标c、φ值的影响差异显著，虽然c、φ值都随着含水率的增大而减小，但两者的减小幅度相差很大，含水率对c值影响很大而对φ值影响相对微小，该结果与文献［1］的统计分析结论一致.由表1可得：当含水率ω＝13%～17%，ω值每增加1%，c值下降6.40%，而φ值仅下降0.21%；当含水率ω＝17%～21%，ω值每增加1%，c值下降13.26%，而φ值仅下降0.42%.在同等条件下，c值降幅达φ值30倍以上.同时，含水率愈高对c、φ值的影响愈大：以最优含水率ωop为界，含水率大于ωop时的c、φ值降幅大约是含水率小于ωop时的2倍.

由图5及表2可知，花岗岩残积土初始变形模量Ei随着含水率和围压σ3的变化呈现一定规律：在围压一定时，Ei随着含水率的增大而减小，其中围压较小（σ3＝100kPa）时，Ei随含水率增大而减小的幅度较大，而且以最优含水率ωop为界，含水率大于ωop时的Ei值减幅大约是含水率小于ωop时的1.4倍；而围压较大（σ3＝200，300kPa）时，Ei随含水率增大而减小的幅度较小，而且基本呈线性关系.在含水率不变时，Ei值随着围压σ3的增加而增大，特别是围压较小时，围压的增加对Ei值的增大影响更显著.

同样地，其余参数也随着含水率的变化而变化.由图6～图8及表2可知：参数K随着含水率的增大而减小，而且以最优含水率ωop为界，含水率大于ωop时的K值减幅大约是含水率小于ωop时的1.2倍；参数n、Rf均随着含水率的增大而增大：对参数n，含水率大于ωop时的n值增幅大约是含水率小于ωop时的1.56倍；对参数Rf，含水率大于ωop时的Rf值增幅大约是含水率小于ωop时的3倍.

说明一点：参数Rf值一般在0.75～1.00之间［8］，表2的Rf值均在0.90以上，表明实验取轴向应变ε1＝15%对应的偏应力作为破坏偏应力（σ1－σ3）f，与极限偏应力（σ1－σ3）u接近，而此实试样除了继续发生鼓胀变形外，并未出现破坏剪切面，体现了土样的应变硬化特性和应变控制破坏的特点.

3 结 语

a.在不同围压和不同含水率条件下，花岗岩残积土击实试样在三向应力作用下均呈鼓胀变形特征，其固结排水应力应变曲线均为加工硬化型，与邓肯－张模型的条件式基本吻合.

b.花岗岩残积土的邓肯－张模型参数随含水率变化的基本规律是：抗剪强度指标c、φ值，初始变形模量Ei及参数K 均随着含水率的增大而减小；参数n、Rf随含水率的增大而增大.

c.除了内摩擦角φ之外，含水率对花岗岩残积土的邓肯－张模型参数整体上影响较大，其中粘聚力c受影响显著，参数n和低围压时的初始变形模量Ei受影响较显著.各参数与含水率关系曲线均在最优含水率ωop处出现拐点，而且当含水率大于ωop时，其对各参数的影响不同程度地加大.

d.试样制作前筛除了2mm以上粗颗粒（占18.8%），必会影响试验结果，但由于土中水主要与细粒土发生作用，因此预计该影响主要表现在参数的大小上，不会改变其应力应变特性及参数的变化规律.

［1］吴能森.结构性花岗岩残积土的特性及工程问题研究［D］.南京：南京林业大学，2005：51－55.WU Nengsen.A study on characteristics and some engineering problems of granite residual soil with structural nature［D］.Nanjing：Nanjing Forestry University，2005：51－55.（in Chinese）

［2］吴能森.花岗岩残积土的崩解性及软化损伤参数研究［J］.河北建筑科技学院学报，2006，23（3）：58－62.WU Nengsen.A study on calving property and softening damage parameter of granite residual soil［J］.Journal of Hebei Institute of Architectural Science and Technology，2006，23（3）：58－62.（in Chinese）

［3］李险峰.含水率对金坪子滑坡土体力学特性的影响［J］.武汉工程大学学报，2012，34（3）：27－31.LI Xianfeng.Impact of moisture content on mechanical properties of Jinpingzi slip soil［J］.Journal of Wuhan Institute of Technology，2012，34（3）：27－31.（in Chinese）

［4］张学言，闫澍旺.岩土塑性力学基础［M］.天津：天津大学出版社，2004：60－65.ZHANG Xueyan，YAN Shuwang.Fundamentals of geotechnics plasticity ［M ］. Tianjin： Tianjin University Press，2004：60－65.（in Chinese）

［5］Kondner R L. Hyperbolic Stress－stain Response：Cohesive soils［J］.Journal of the Soil Mechanics and Foundations Division ASCE，1963，89（SM1）：115－143.

［6］Duncan J M，Chang C Y.Nonlinear analysis of Stress and Strain in Soils［J］.Journal of the Soil Mechanics and Foundations Division ASCE，1970，96（SM5）：1629－1653.

［7］水利部南京水利科学研究院.GB／T 50123－1999土工试验方法标准［S］.北京：中国计划出版社.Nanjing Hydraulic Research Institute.GB／T 50123－1999Standard for soil test method［S］.Beijing：China Planning Press.（in Chinese）

［8］胡中雄.土力学与环境土工学［M］.上海：同济大学出版社，1997：146.HU Zhongxiong.Soil mechanics and environmental geotechnics［M］.Shanghai： Tongji University Press，1997：146.（in Chinese）