我国区域高等教育水平的综合评价
2013-10-21张海英周志刚
张海英,周志刚,刘 星
(1.天津大学管理学院,天津 300072;2沧州师范学院,教育系 061001)
0 引言
随着我国经济发展区域化和高等教育地区化的进一步深入,高等教育作为形成人力资本的重要途径,引领科技创新、推动经济发展的重要力量,逐渐成为区域经济发展的核心要素之一。如何提升区域高等教育的实力;以及如何缓解供需矛盾,确保有限资源的有效合理利用,最终提高区域高等教育水平,缩小区域差距、促进区域经济长足增长,有着重要的研究意义。
本文以我国31个省区的高等教育为研究对象,在合理选取测度指标的基础上,应用因子分析法和改进的DEA法分别测度高等教育的实力、效率,建立区域高等教育水平的二维综合评价矩阵,并展开分类评价,以求较全面地刻画我国区域高等教育水平的发展现状,为国家及区域经济的战略发展提供有益参考。
1 变量与数据
区域高等教育水平是区域高等教育的发展水平,达到的程度,属于一个比较的概念(刘智运,2009),它既与高等教育的投入产出的数量有关,也与投入产出的质量有关。而前人研究高等教育实力实质上只关注了高等教育水平“量”的比较,研究高等教育效率只关注了其“质”比较。为了全面、准确地表达区域高等教育水平,本文将结合以往研究的成果,并考虑到数据的可获性,拟从高等教育投入、高等教育产出两个方面、17个指标,构建衡量高等教育水平“量”的高等教育实力和“质”的效率指标体系。
高等教育投入是高等教育赖以存在和发展的物质基础,涉及到人力、财力、物力等方面,可量化为以下9个指标。首先,高校教师的数量和质量是高等教育发展的关键因素,因此选择各省区高等学校专任教师数、各省区高等学校专任教师博士比例、各省区每十万人口拥有大学教授数作为人力投入指标。其次,我国高等教育教育经费的来源目前仍主要来自政府财政拨款,故选择各省区高等教育生均预算内教育经费支出、各省区预算内高等教育经费占其财政支出比例情况、各省区高等学校生均教育经费支出等来反映我国区域高等教育的财力投入情况;最后,物力投入一般为具有长期使用价值的存量资产,代表性的指标有各省区生均学校产权校舍建筑面积、各省区生均固定资产、各省区生均教科研仪器设备价值。
高等教育的产出则被公认反映在人才培养、科学研究、社会服务三方面,分别选取以下的8个指标:各省区每十万人口在校本、专科学生,各省区每十万人口拥有在校研究生数,各省区在读外国留学生数,各省区平均每所高校在校生数,高等学校R&D课题及S&T课题的总数,各省区高校属国家重点实验室和国家重点学科数量,各省区拥有“211工程”学校数,各省区拥有“985工程”学校数。
本文指标数据主要来自《中国教育统计年鉴(2008)》、《中国教育经费统计年鉴(2009)》、《中国科技统计年鉴(2009)》及中国学位与研究生网、搜数网等网站。
2 区域高等教育水平综合评价模型
2.1 区域高等教育实力的测算
本文拟建立因子分析模型计算各省区高等教育的实力。因子分析法(Factor Analysis Approach)是一种多元统计方法,其基本思想是通过对相关矩阵或协方差矩阵的内部依赖关系的研究,在最少信息丢失的前提之下,将多个变量综合为少数几个相互独立的主因子,最终达到降维目的。其数学模型如下:

其中X=(X1,X2,…,Xp)是可观测的 p维随机向量,其均值 E(X)=μ,协方差阵Cov(X)=Σ 。 μ=(μ1,…,μp)'为X的均值向量,F=(F1,…,Fm)'(m<p)为不可观测的随机向量,且 E(F)=0 ,Cov(F)=Im,ε=(ε1,…,εp)'满足 E(ε)=0 ,Cov(ε)=D ,Cov(ε,F)=0 。(1)用矩阵表示为:X=μ+AF+ε。AF表示m个主因子能解释的部分,ε表示含信息量很少的残余部分。Fi(i=1,…,m)为主因子,εi(i=1,…,p)为特殊因子,矩阵 A=(aij)p×m为因子载荷阵。本文通过对投入和产出组成的区域高等教育实力指标体系提取的少量主因子,使其能够反映原有多个变量所反映的绝大部分信息,具有较强的解释能力。最后各项因子得分加权汇总,得到代表各省区高等教育实力的综合得分,用Fα表示,

其中di为第i个主因子方差贡献率,Fα(i)为第α个省区在第个i主因子的得分。
2.2 区域高等教育效率的测算
2.2.1 DEA评价模型
数据包络分析(Data Envelopment Analysis,简称DEA)方法由Charnes和Cooper、Rhodes于1978年首先提出,是一种旨在评价多投入、多产出的若干个同质决策单元(DMU,decision making unit)相对有效性的非参数统计方法。DEA方法排除了很多主观的因素,具有很强的客观性,被广泛运用在各个领域中。较为常用的是假设规模报酬不变的CCR模型:
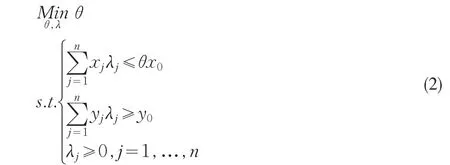
其中,xj为第 j个决策单元的m维投入向量,yj为第 j个决策单元的s维产出向量。x0、y0是被评价的某决策单元DMUj0的投入、产出向量。λj为投入产出指标权系数,θ为DMUj0的相对效率衡量指标。θ介于0与1之间,当θ=1时表示该决策单元DEA有效;而当θ<1时则表示DEA无效。当加入限定条件∑λj=1时,则表示规模报酬变动,即为BCC模型。由CCR模型、BCC模型可计算出总效率值和技术效率值,且总效率可以分解成技术效率和规模效率,表达式为总效率=规模效率×技术效率。
2.2.2 对投入产出指标的降维处理
在实际应用中,传统DEA模型存在着一定的局限性,比如模型对指标数量与样本数量有一定的要求。决策单元样本数量有限而指标过多则会导致DEA模型辨识能力下降,会有过多的决策单元被判断为DEA有效,影响了评价的准确性。就此,Cooper等(2000)指出关于DEA模型选择投入、产出指标数量的首要规则要求:n=max{m×s,3×(m +s) },n为决策单元的样本容量,m和s分别为投入和产出指标的数量。在此基础上,很多学者提出了改进的方法,以求同时达成通过更多的指标信息全面反映待评问题和提高DEA辨识能力两方面的要求。
对于本次评价中存在的同类问题,本文尝试运用因子分析技术,分别对投入、产出指标进行降维处理,以能在尽量保持原指标体系信息量的前提下,减少评价指标总数,降低指标间的相关性。将投入、产出的主因子及各项主因子得分作为DEA模型的新的投入、产出指标和数据,进行DEA效率分析,并得到各省区高等教育效率值θα(α=1,…,n)。
2.3 综合评价模型
以区域高等教育实力Fα为纵坐标,以区域高等教育效率θα为横坐标,绘制区域高等教育水平综合评价矩阵图,如图1所示。

图1 区域高等教育水平综合评价矩阵θa
对于第α个省区其高等教育实力综合得分Fα,若大于均值则认为该省区高等教育实力较强,反之,则较弱。同样,第α个省区的高等教育效率θα,若大于其均值,则认为该省区高等教育效率较高,反之,则较低。以为界,图1中各个省区被划分入Ⅰ、Ⅱ、Ⅲ、Ⅳ四个代表不同高等教育水平的区域。其中Ⅰ区表示区域高等教育的水平高,Ⅱ区、Ⅲ区表示区域高等教育水平较高,Ⅳ区表示区域高等教育水平较弱,各个省区可以据此考察其高等教育实力与效率所处水平,进而施以不同路径和力度的改善,以提高本区域的高等教育水平。
3 实证分析
3.1 区域高等教育实力的测算
本文运用R软件,对2008年我国各省区高等教育实力的17项指标进行因子分析条件检验;计算其特征根、方差贡献率及累积方差贡献率;确定主因子个数为3,其方差贡献率为0.8985;采用方差最大的正交旋转法和regression法提取因子后,计算各省区和东中西部地区综合得分及排名情况,如表1所示,其中东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东、海南11个省区;中部包括山西、内蒙古、吉林、黑龙江、安徽、江西、河南、湖北、湖南9个省区;西部包括广西、重庆、四川、贵州、云南、陕西、甘肃、青海、宁夏、西藏、新疆11个省区。计算全国范围内各省综合得分均值

表1 各省区高等教育实力综合因子得分及排名情况
3.2 区域高等教育效率的测算
由于投入指标数为9,产出指标数为8,样本容量为31,此时决策单元样本容量与指标数量不满足Cooper等所提出的原则,会严重影响DEA的辨识能力,需要对2008年我国各省区高等教育的投入指标和产出指标分别进行降维处理,各自提取主因子,将其因子得分进行非负变换后,建立新的指标体系(见表2),投入与产出指标均减少到3项。对于区域的高等教育系统,投入要比产出更容易实现控制,因而运用DEA Excel Solver对新建指标体系进行以投入为导向的DEA分析,结果如表3所示,计算总效率均值
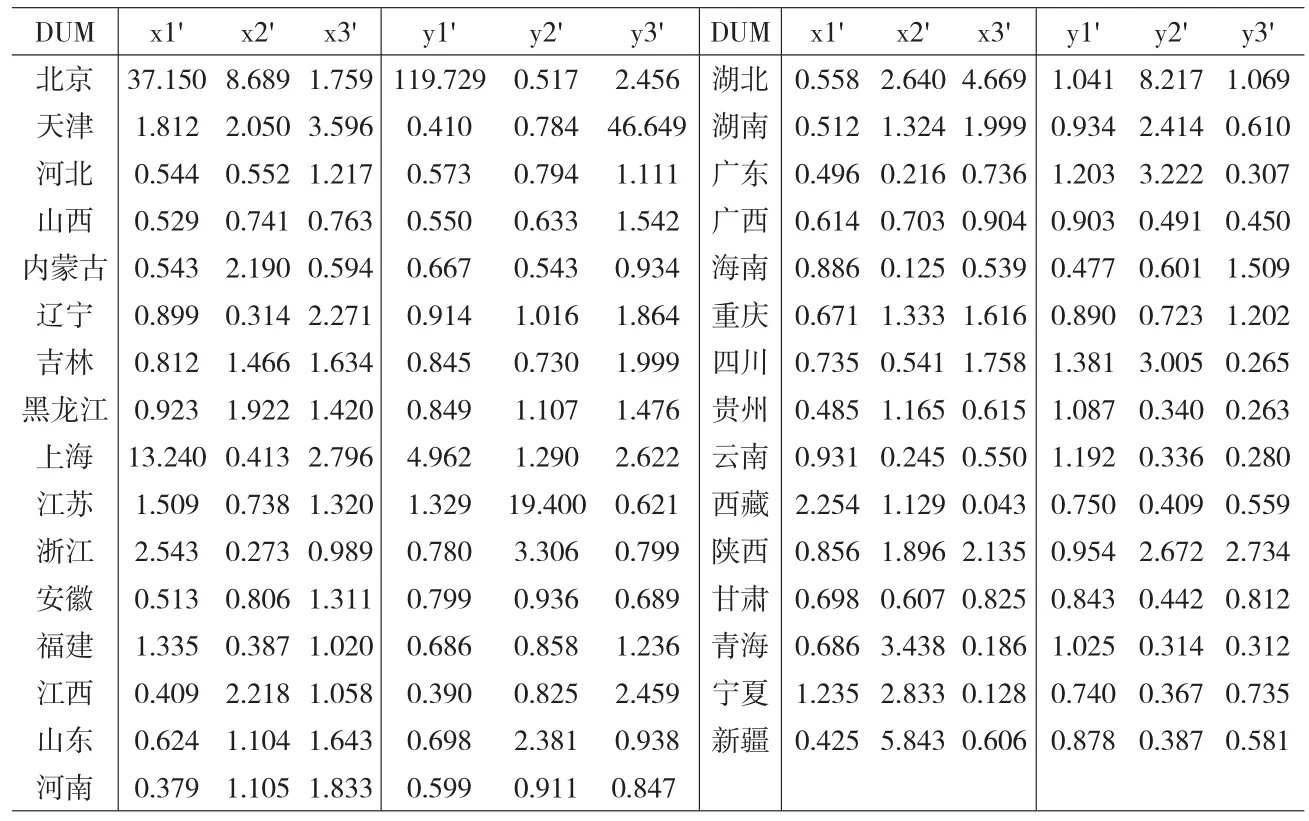
表2 因子分析处理后的各省区高等教育投入产出指标体系X'、Y'
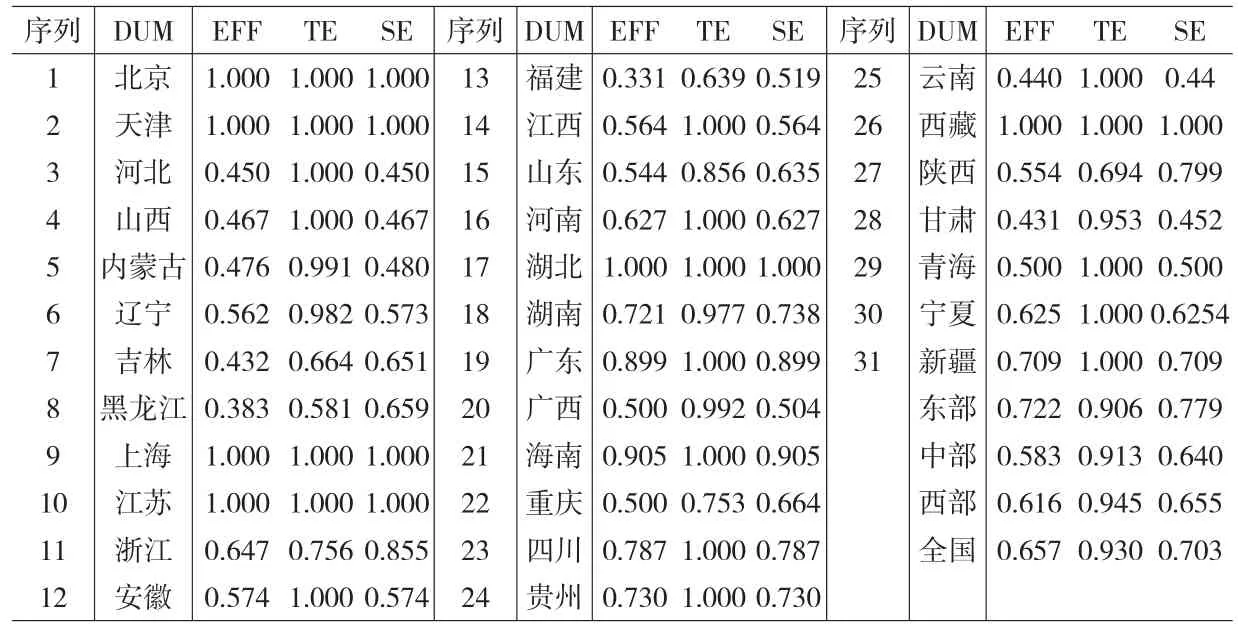
表3 各省区高等教育效率θa
3.3 区域高等教育水平的综合评价
运用R软件将所得的各省区高等教育实力与高等教育效率(EFF总效率)数据画图,并以为界进行分区,得到区域高等教育水平综合评价矩阵图(见图2)。
3.4 区域高等教育水平分析
从高等教育实力维度考察,结合图2与表1可观察到,全国高等教育实力较强的区域有北京、上海、江苏、天津、湖北、广东、浙江、陕西、辽宁、黑龙江、四川、山东等12个省区,其他19个省区高等教育实力较弱。从东中西部比较来看,东部高等教育实力均值显著高于全国平均水平,及中、西部。总体上,全国高等教育实力的分布以向东部、向发达地区聚集为特征,呈现出显著的不均衡,多与区域经济的发展、我国城市化进程、政治政策、教育体制等多种因素有关。
从高等教育效率维度考察,由图2与表3可知,北京、上海、江苏、天津、湖北、西藏等6个省区即高等教育总效率值为1,为DEA有效区域,这些地区能够较充分地利用教育这一稀缺资源;其他25个省区高等教育总效率值小于1,为DEA无效,特别是河北、山西、黑龙江、内蒙古、福建、云南、甘肃等省区高等教育总效率不足0.5,DEA效率低下,这些省区必须重新审视其资源利用情况,进一步合理配置高等教育资源。从东中西部比较来看,东部高等教育总效率为0.722,显著高于全国平均水平及中、西部地区。全国高等教育总效率平均水平为0.657,表明我国高等教育资源有效利用情况总体尚处于较低水平,经过效率分解后,全国平均技术效率为0.930,说明受到组织、管理、制度水平的影响,高教系统中存有一定的教育资源浪费现象。同时由于全国平均规模效率均值为0.703明显低于技术效率,说明现阶段我国高等教育的大众化普遍存在着教育资源投入严重不足问题,势必影响高等教育总效率的水平。从综合的角度来观察,可以将我国各区域的高等教育水平可分为四个不同的类型。第一类区域高等教育水平高,位于综合评价矩阵图的Ⅰ区,有北京、上海、天津、江苏、湖北、广东等7省区。这些省区高等教育的实力强,效率高,应保持和增进现有水平,充分发挥其高等教育领域的头羊作用,通过区域间高等教育的合作,带动其他区域高等教育的发展。
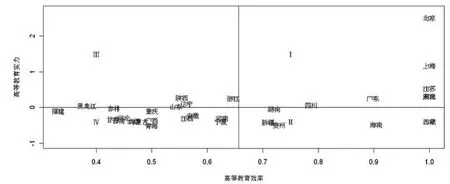
图2 区域高等教育水平综合评价矩阵图
第二类区域高等教育水平较高,位于Ⅱ区,包括湖南、海南、新疆、西藏、贵州等5省区,相对于Ⅰ区,这些省区高等教育实力较弱,但效率却很高,应是高等教育发展的重点支持区域,需优先考虑从增强区域高等教育实力入手,以充分发挥其效率优势以提升其高等教育的水平。
第三类区域高等教育水平较高,位于Ⅲ区,有陕西、浙江、山东、辽宁、黑龙江等5省区,但与第二类不同的是,这些省区高等教育的实力较强,效率却不理想,故应转变以大规模投入为基础的粗放式高教发展模式,在有效调整研发投入的同时,适当的进行制度变革和管理创新,以提高资源的利用效率。
第四类为高等教育水平较弱的区域,位于Ⅳ区,有福建、甘肃、河北、河南等14省区,这类区域的特点是高等教育实力较弱,效率也不高。此类地区需要一方面合理的增强高教实力,集中有限资源解决高等教育发展的关键问题,另一方面给与适当的政策和资金扶持,改善高等教育发展环境,增进高等教育效率。
值得提出的是,不仅不同类别之间的省区,其高等教育水平调整的力度和路径不尽相同。而且对同一类别的省区而言,也需结合其具体情况,选择不同的调整方案。以同处Ⅰ区的北京、广东、四川为例,它们高等教育水平都很高,但北京高等教育实力最强,并且属于DEA有效区域,在既定规模下,可保持原有投入产出及效率水平。而位于其左下方的广东需在高等教育的实力和效率两方面做出小幅的改善,四川省则需为改善这两方面付出更大的努力。
另外,图2还表明高等教育实力较强的省区,投入、产出很高,但其高等教育资源配置相对有效性不一定高;反之,高等教育实力较弱的省区,其高等教育资源配置相对有效性不一定低。以位于Ⅱ区的山东省为例,其高等教育实力较高,但效率值却低于全国平均效率水平;而位于Ⅲ区的西藏虽然高等教育实力较弱,但DEA效率值为1。由此可见,各省区只有统筹兼顾高等教育实力和高等教育效率两个方面,才能有效保证区域高等教育的健康发展并实现区域高等教育水平的稳步提高。
4 结论与建议
本文应用因子分析法和改进的DEA法,从高等教育实力和高等教育效率,构建二维综合评价矩阵,来刻画我国各区域高等教育水平并进行了相应的综合评价和实证分析。结果表明,目前我国区域高等教育实力分布不均衡,而且高等教育效率水平总体偏低,区域的高等教育水平大致可以分为四个不同的类型,并存在着显著的差异。要改善这些现状,一、各省区应始终坚持高等教育优先发展的战略地位,完善投入机制,积极地拓宽高等教育投入的渠道,科学地加大高等教育的投入,重点发展和扶持区域高等教育水平较低的省区。二、推进跨区域高等教育合作,加强东部地区与中西部地区高等教育资源的整合与协调,缩小区域间高等教育发展的差距。三、有必要制定因地制宜的高等教育发展战略,既要注重区域高等教育外延的发展,也要注重其内涵的提高。由于各区域经济社会发展的优势与着力点不同,对各类内、类间的省区的高等教育改善的路径和力度也不同。各区域应避免走入盲目求大求强,趋同发展的误区,发掘自身高等教育优势,抓住发展契机,解放思想,以特色提升高等教育水平,实现多样性高等教育和谐共生,共同发展。四、各省区还应深化改革创新现有高等教育管理体制和育人模式,促进现代大学制度的建立,确保高效地配置教育资源,加快科研成果的转化,提高人才培养的质量,从而提高区域高等教育自身的生产力。
[1]杨明.中国高等教育实力在世界的定位[J].浙江大学学报(人文社会科学版),2003,(5).
[2]杨明.中国教育实力在世界的位置[J].比较教育研究,2000,(1).
[3]籍艳丽.我国区域高等教育的实证研究[J].山西财经大学学报(高等教育版),2006,(4).
[4]刘丽.区域高等教育发展实力分析[J].教育发展研究,2009,(19).
[5]崔玉平.省域高等教育实力的分类评价[J].清华教育研究,2010,(1).
[6]Charnes,A Cooper,W W,Rhodes,E.Measuring the Efficiency of De⁃cision Making Units[J].European Journal of Operational Research,1978,2(6).
[7]Cooper,W W,Seiford,L M,T one,K.Data Envelopment Analysis:a Comprehensive Text with Models-Applications,References and DEA-Solver Software[M].Boston:Kluwer Academic Publishers,2000.
