基于分数Vasicek随机利率模型的保本基金定价研究

付秀艳,刘蕾蕾，陶祥兴,黄文礼

(1.宁波大学 理学院，浙江 宁波 315211；2.中央财经大学 金融学院，北京 102206;3.浙江科技学院 理学院,杭州 310023)

基于分数Vasicek随机利率模型的保本基金定价研究

付秀艳1,刘蕾蕾2，陶祥兴3,黄文礼3

(1.宁波大学 理学院，浙江 宁波 315211；2.中央财经大学 金融学院，北京 102206;3.浙江科技学院 理学院,杭州 310023)

讨论了在分数金融市场环境下，与股票价格指数相关的分红保本基金的定价原理和方法，并且通过风险对冲、随机过程和偏微分方程的方法，推导出了分数Vasicek随机利率模型下与股指挂钩的分红保本基金定价公式，且给出了保本基金的显式解。

保本基金;分数金融市场;风险对冲;偏微分方程;随机利率模型

近年来，股票市场的不景气促使投资者不得不开辟新的投资渠道。投资者既想在一定比例上约束投资最低收益，又想使投资组合收益最大化，这就促成了保本基金的产生。保本基金(Segregated Fund)是指在一定投资期限内，对投资者所投资的本金提供一定比例保证保本的基金，它是一种创新的基金品种。首先要清楚保本基金的设计理念，它是把利息或小部分资产投资于杠杆率比较高的金融产品，而这些金融产品虽然收益较高但风险也较大，如股票、衍生证券、期货等；同时把大多数基金资产投资到低风险收益稳定的金融产品如债券、国债等，这样可以保证基金的大部分收益都是稳定的，且不用承担高风险。因此，即使市场不景气，投资环境比较差，投资结果也会达到预期的保本作用，兑现当初对投资者的承诺。

根据保本基金的设计原理可以看出，对于投资市场波动比较大、走势不容易判断，或者风险厌恶型的投资者，保本基金会是一个较为适合的投资选择。它很好地抓住了投资者的心理，让他们无后顾之忧，不用担心承担很大的损失，因为通过投资保本基金既保证了一定比例本金的收取，又有机会获得基金高风险部分的投资收益。基于此，保本基金备受投资者的欢迎。尤其是在近几年，股票市场行情不明朗且银行存款利率又不理想的情况下，保本基金备受市场和投资者的追捧，它将成为一种新的理想避险品种。然而，保本基金并不是无条件和绝对百分之百的保本，它存在期限上的约束。需要说明的是保本基金有一个重要的特征——半封闭性，即如果投资者在基金没有到期就解除合约，那么投资者将得不到当初的保本比例及投资收益，而且还会承担违约所造成的费用。

基于近几年中国股市的动荡，投资者急于寻求相对稳定的投资途径，保本基金一时间发展迅速，在投资市场所占份额日益增加。中国国内第一只保本基金“南方避险增值基金”于2003年5月发行，且行情看好，成交量不断增加。2004年2月，“银华保本增值基金”发行，随后中国又连发3只保本型基金。在经历了2005年以后的停滞阶段后，保本基金在2010年又迎来新的发展契机。根据《关于保本基金的指导意见》[1]的发布，可以看出保本基金深受国家各有关部门的重视和支持，相信关于保本基金的相关法律法规将不断被完善，它将会迎来更好的运行环境。Wind数据显示，截至2012年10月18日，市场上保本基金的数量已达33只，总规模超过600亿元[2]。保本基金在国内的基金行业占据了一定的地位。

2012年以来A股市场震荡剧烈，投资者叫苦不迭，从而纷纷将资金转向低风险产品。受此影响，以“攻守兼备”著称的保本基金悄然扩容，迎来了新的发展契机。Wind数据显示，截至2012年10月份，年初以来成立的13只保本基金，首募总规模达237.83亿元，平均单只募集规模为18.29亿元[2]。而旗下已拥有3只保本基金的南方基金上演“保本不断档”，近期推出了第四只该类产品——南方安心保本基金。在A股震荡筑底而债市水涨船高的情况下，保本基金扩容之势将延续。

在当前保本基金蓬勃发展的大趋势下，对其合理设计与公正定价是应形势之需，对金融市场的发展具有很重要的现实意义。本研究基于分数Vasicek金融市场模型，考虑与股票价格指数相关的分红保本基金的设计原理和定价方法，推导得出了定价公式。

1 预备知识

1940年Kolmogorov[3]首次在Hilbert空间中定义、研究了分数布朗运动,命名为Wiener。1968年，Mandelbrot和Van Ness第一次提出了分数布朗运动的概念,以下是本研究要用到的相关定义和引理，可为后面保本基金的定价公式推导做理论铺垫。

定义1.1[4]设概率空间(Ω,F,P)，具有Hurst参数为H∈(0,1)(H为一个常数)的分数次布朗运动是一个连续的高斯过程BH={BH(t)∶t≥0}={BH(t,ω)∶t≥0,ω∈Ω}，且满足以下条件：

1)BH(0)=E(BH(t))=0,(t≥0);

式中，E是关于概率测度P的期望；且当H=1/2时，BH(t)就为标准型布朗运动。

分数次布朗运动为自相似过程，且当H∈(1/2,1)时具有长期依赖性，即对所有n=1,2,…，有

分数次布朗运动的这些性质在应用数学及金融工程方面都是非常有用的工具。本研究假设H∈(1/2,1)。

对于一个恒定的H∈(1/2,1)，定义φ(t,s)=H(2H-1)|t-s|2H-2,t,s∈。

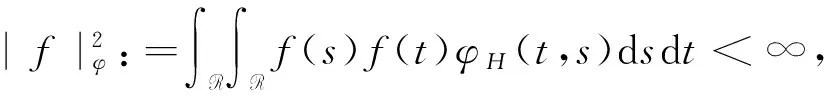
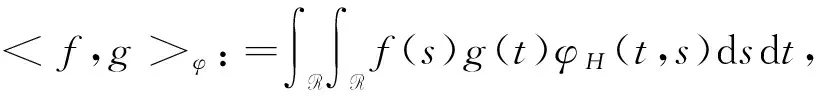
设BH(t)为概率空间(S′(R),F,P)中的分数布朗运动，其中Ω:=S′(R)为R上的减速函数Schwarz空间S(R)的对偶空间。

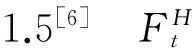
根据定义1.5不难证明如下引理:

引理1.21)BH(t)是拟鞅；

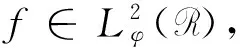
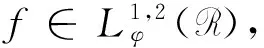
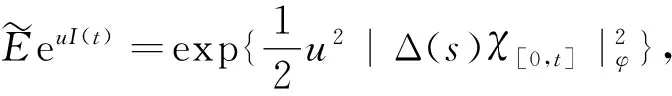
(1)

因为Δ(s)不是随机的，故式(1)就等价于

(2)

综上，就得到了式(2)。

2 数学模型

2.1 基本假设

1) 金融市场不存在套利机会。

2) 金融市场无摩擦，无税收，无交易费。

3) 资产的构成为每份基金面值1元人民币。针对中国的实际情况，特设以下条款：

a.基金到期时的保底收益是每份α元，对于超额收益部分将进行分红，且比例是β(0≤β≤1)；

b.基金全部投资于指数基金，如股票价格指数。

4) 此处，假设指数基金的净值服从分数几何布朗运动，即：

(3)

另外，采用服从分数Vasicek随机利率模型作为这里的市场利率模型，即：

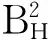
5) 设保本基金的价值C是与时间t、利率rt和指数基金价值St有关的函数，即Ct=C(St,rt,t)。

2.2 数学模型建立

现在假设(ΩF,Ft,P)是具有σ-流的一个概率空间，BH={BH(t),t≥0}是(Ω,F,P)上的分数次布朗运动，Ft是由F所生成的σ-代数流，P是风险中性测度。假设It型分数Black-Scholes市场上只有三类证券,即有风险的标的资产、标的资产的期权与零息票债券，并且记在T时刻到期的零息票债券的价格为Pt=P(r,t;T)。

现有这样的一个投资组合，它包括一份价值为C(S(t),r,t)保本基金、Δ1t份的标的资产S(t)，以及Δ2t份零息债券P(t)，则该资产组合在t时刻的价值为

Πt=Ct-Δ1tSt-Δ2tPt

应用多维分数型It公式，得到如下公式

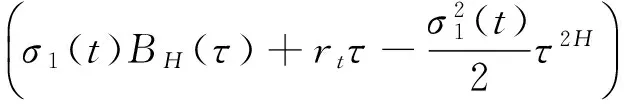
且有

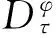
(4)

在[t,t+dt]内有

dΠt=dCt-Δ1tdSt-Δ2tdPt

(5)

为了消除式(5)中的随机项,分别取[8]:

代入式(5)， 得

dΠt=dCt-Δ1tdSt-Δ2tdPt

由无套利原理可知

E(dΠt)=r(t)Πdt=r(Ct-Δ1tSt-Δ2tPt)dt，

结合式(5), 得到了分数Vasicek随机利率下分红保底基金的价值Ct所满足的定价方程

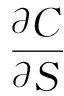
由于有银行提供担保，因此这里就不存在违约的可能性，于是，这里的定解就转化为

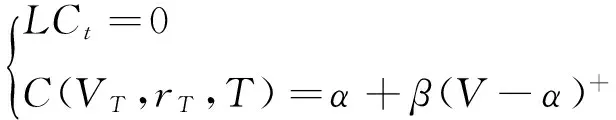
经过运算，最终可以得到

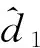
其中

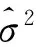
3 结 语

本研究虽然推导得到了分数Vasicek金融市场下保本基金的显式解，但是在现实金融市场中，模型中的假设条件并不能完全满足，比如交易费用；另外一个值得考虑的问题是，保本基金的担保，中国目前发行的保本基金是需要第三方进行担保的，当无担保时，若基金投资市场低迷，发生损失，则基金发起人要兑现当初的保本收益承诺就必须以自有资金来承担投资损失，否则也是对保本基金的违约，在这种情况下，之前的设计条款就不再适用，需要重新设计，再建立新的模型对保本基金定价。

[1] 中国证券监督管理委员会.证监会公告[2010]30号——关于保本基金的指导意见[EB/OL].(2010-06-20)[2012-11-26].http://www.csrc.gov.cn/pub/zjhpublic/G00306201/201011/t20101101_186102.htm.

[2] 叶子.保本基金悄然扩容 南方基金上演“保本不断档”[N].中山商报，2012-10-23(B2).

[3] Kolmogorov A N. Wienersche Spiralen und einige andere interessante Kurven im Hilbertschen Raum[J].Comptes Rendus(Doklady)de L′Académie Des Science de L′URSS,1940,26:115-118.

[4] Black F, Scholes M S. The pricing of option and corporate liabilities[J].Journal of Political Economics,1973,81:637-659.

[5] Vasicek O. An equilibrium characterization of the term structure[J].Journal of Financial Economics,1997,5:177-188.

[6] Lando D. Credit Risk Modeling: Theory and Applications[M].New Jersey: Princeton University Press,2004:119-121.

[7] 黄文礼，陶祥兴，李胜宏.分数维Vasicek利率模型下的欧式期权定价公式[J].数学学报，2012,55(2):199-230.

[8] Necula C. Option pricing in a fractional Brownian motion environment[J].Mathematical Reports,2004,6(3):259-273.

PricingresearchforsegregatedfundunderfractionalVasicekstochasticratemodel

FU Xiuyan1, LIU Leilei2, TAO Xiangxing3, HUANG Wenli3

(1. Faculty of Science, Ningbo University, Ningbo 315211, China; 2. School of Finance, Central University of Finance and Economics, Beijing 102206,China; 3. School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China)

We propose the design principle and pricing method about dividend segregated fund related to stock index under the background of fractional financial market.We have the pricing formula of dividend segregated fund related to stock index under fractional Vasicek stochastic rate model, making use of risk hedging,stochastic process and partial differential equation,and obtain explicit solution finally.

segregated fund; fractional financial market; risk hedging; partial differential equation model; stochastic rate model

O211.5;F224.0

A

1671-8798(2013)01-0001-05

10.3969/j.issn.1671-8798.2013.01.001

2013-01-06

国家自然科学基金资助项目(11171306)

付秀艳(1987— )，女，安徽省阜阳人，硕士研究生，研究方向为金融数学。

陶祥兴，教授，博士，主要从事调和分析与偏微分方程研究。