瑞利衰落信道下扩频信号隐分集性能分析
2013-10-20刘丽哲沈斌松
刘丽哲,沈斌松
(中国电子科技集团第五十四研究所,河北石家庄 050081)
0 引言
瑞利衰落信道是一种无线电信号传播环境的统计模型。无线电信号通过这种信道到达接收端后,具有显著的快衰落特征,衰落幅度(10%时间与90%时间被接收信号电平超过的电平分贝数之差)高达13.4 dB,严重影响了通信质量[1,2]。为了有效克服信号衰落,工程上常采用分集接收技术,即利用信号的空间选择性、频率选择性和时间选择性等,将所需要传送的信息复现成若干个基本独立的信号,收端将之合并,使信号相互弥补和加强,从而达到平滑信号衰落,保证信息平稳传输目的[3,4]。按照分集信号获取方式,分集接收技术分为2类:一类是诸如空间分集、频率分集的显分集技术,依靠增加设备通道数实现;另一类是隐分集技术,在不增加设备通道数的基础上,通过巧妙的信号波形设计实现。
隐分集技术因其具有简化设备的优越性,在工程设计中得到青睐,其中采用扩频信号的失真自适应接收机(Distort Adaptive Receiver,DAR)就是一个典型实例。这种接收机能够将接收到的扩频信号在时域压缩成窄脉冲并分离出衰落独立的多径信号,经合并处理后获取可观的隐分集增益[5],且隐分集增益与多径时延功率谱和合并方式密切相关,至今未见通用公式,针对扩频信号的DAR,提出了一种适用于瑞利衰落信道的扩频信号隐分集增益分析方法。
1 扩频信号的DAR隐分集获取原理
工程中常用的扩频信号主要有随机序列直接扩频(DS)和线性调频(Chirp)扩频2种方式,两者在波形设计方面各有优势:DS解扩简单,扩频序列多样,便于频谱复用,但其多径分辨能力仅为2/B(B为扩频后信号带宽);Chirp解扩较为复杂,而且扩频样式仅有2个,但其多径分辨能力强,为1/B,是DS 的一倍[6,7]。因此,在实际工程应用中,应根据具体的应用场合灵活选择。
虽然2种扩频方式分辨多径能力和解扩方式不同,但二者的接收处理流程和DAR工作原理相同,分别如图1和图2所示。
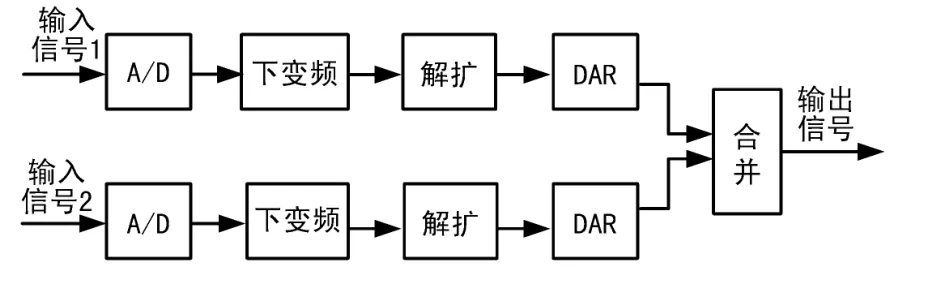
图1 扩频信号的接收处理流程图
图1以2重显分集为例,假设系统设计能分辨出2个多径,则两路中频输入信号分别依次经A/D采样、下变频和解扩处理后,得到时域压缩、多径分离的窄脉冲信号,如图2所示。在后续DAR中,采用逆调制方式提取与窄脉冲信号同频、同相、同包络的载波信号,并将之与窄脉冲信号进行鉴相、积分处理,实现匹配接收,即最佳接收功能。另外,每个显分集支路的各个衰落互相独立的分离多径分量,经过鉴相、合并处理后,能量累积起来,从而获取隐分集增益,每个多径等效一重显分集;多个显分集支路合并为最大比值合并。

图2 扩频信号的DAR工作原理图
2 扩频信号隐分集性能分析
2.1 系统模型
瑞利信道采用分集接收技术的系统离散时间模型如图3所示。

图3 瑞利信道系统离散时间模型
假设有M个显分集通道传送携带相同信息的信号,各个分集通道的衰落过程hm(t),(m=1,2,…M)是相互独立的;各个分集通道受到相互独立的零均值加性高斯白噪声 nm(t),(m=1,2,…M)的干扰,并且各个分集通道的高斯白噪声具有相同的功率谱密度N0。
假设各分集通道的时延功率谱一致,均为离散的L径结构,则信道响应hm(t)可表示为[8]:

式中,am,k(m=1,2,…M;k=1,2,…L)为第 m 个分集通道中多径k的衰落因子,服从瑞利分布,并且满足:

φm,k(m=1,2,…M;k=1,2,…L)为第 m 个分集通道中多径k的相移因子,服从[0,2π]的均匀分布;
τm,k(m=1,2,…M;k=1,2,…L)为第 m 个分集通道中多径k的时延参数。
信道响应确定后,各个分集通道的接收信号可以表示为:
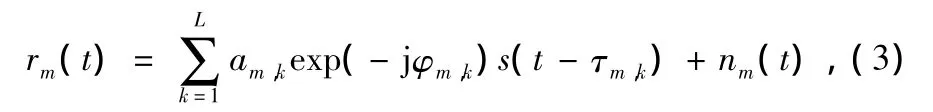
当信号的比特能量为Eb时,各个分集通道接收信号的平均归一化信噪比可以表示为:

式中,Eb/N0为每分集支路归一化信噪比。
2.2 单接收通道下最佳接收性能
当只有一个接收通道时,接收信号表示为:
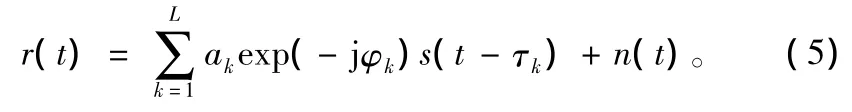
假设各个多径分量的衰落因子服从相同参数的瑞利分布(等强多径),即满足:
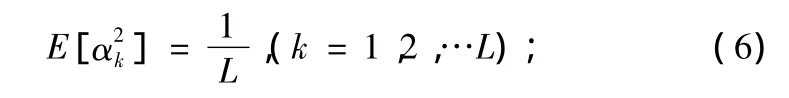
则分离出的L条多径分量最大比合并后的瞬时归一化信噪比γb可以表示为[9]:
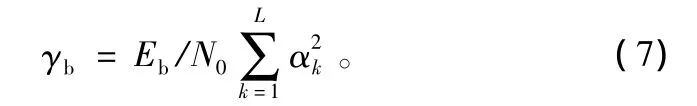
其概率密度函数可以表示为[10]:

根据BPSK/QPSK平均误码率公式,可知,在单接收通道、等强多径选衰信道下BPSK/QPSK的平均误码率表示为[11]:
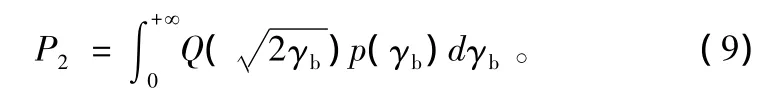
现实中,瑞利信道的各个多径分量的强度并不相等,而是服从瑞利分布,并且满足:
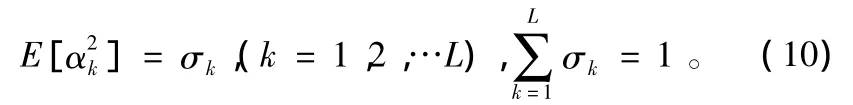
此时,L条多径分量最大比合并后的瞬时归一化信噪比γb则由式(8)变为:
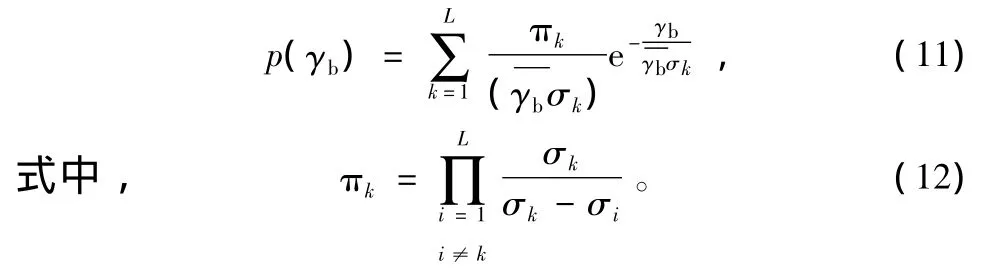
分别将式(8)和式(11)代入式(9)得到3、5、7径等强与不等强(各多径强度如表1所示)时,BPSK/QPSK的平均误码率曲线,如图4所示。

表1 多径强度分布

图4 单通道多径选衰信道下平均误码率曲线
由图4可以看出,单通道多径选衰信道下,扩频信号获取了可观的隐分集增益,且分离多径越多,隐分集增益越大,如多径由3个增加为5个时,1×10-5误码率处的隐分集增益增加约4 dB;相同多径条件下,多径等强比不等强多径的隐分集增益大,如1×10-5误码率处约大1 dB。
2.2 多接收通道下最佳接收性能
当系统有m个接收通道时,接收信号可用式(3)表示,现假设各个分集通道的多径分量衰落因子仍服从瑞利分布,并且满足:

分离接收信道的M×L条多径分量并将各个多径分量最大比合并后的瞬时归一化信噪比γb的概率密度函数可以表示为:
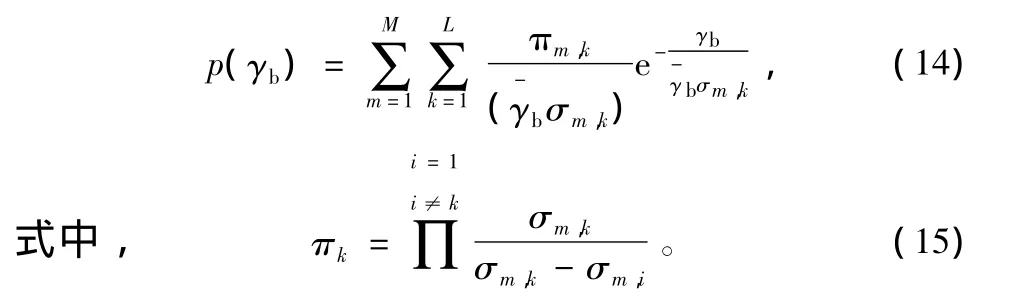
分别将式(14)代入式(9)得到3、5、7径不等强(各多径能量如表1所示)时,BPSK/QPSK的平均误码率曲线,如图5所示。

图5 分集接收信道下BPSK/QPSK平均误码率曲线
由图5可知,多重分集接收的多径选衰信道下,扩频信号的隐分集依然可观。值得说明的是,由于分集重数的增加会使分集改善效果越来越小,因此,图5中多径个数发生相同变化时,4重显分集条件下的隐分集增益要小于2重显分集条件下的隐分集增益。
3 实例测试
搭建具有2重显分集通道的通信系统测试平台,在瑞利信道条件下,测试扩频信号DAR在不同多径时延功率谱时的误码性能,从而验证上述隐分集性能分析的正确性。
系统主要技术指标如下:①传输速率:256 kb/s;②扩频带宽:20 MHz;③多径分辨能力:0.05 μs;④分集重数:2重;⑤解调方式:DAR相干解调。
信道多径时延分别为0.25 μs和0.4μs,多径能量分布分别选用表1中的5径和7径模型,实测误码与理论误码对比曲线如图6所示。由图6可知:当多径时延为0.25μs时,系统能分辨出5条多径,当信噪比小于10 dB时,其隐分集效果低于5径理论曲线,这是低信噪比下工程性能损失大导致;当信噪比高于10 dB时,实测曲线与5径理论曲线平行,达到其隐分集效果;
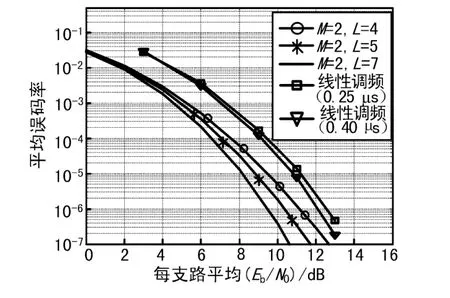
图6 二重分集选衰信道下平均误码率实测曲线
当多径时延为0.4μs时,设置的7条多径均能被系统分辨出,当信噪比小于10 dB时,其隐分集效果优于5径理论曲线,但达不到7径理论曲线;当信噪比高于10 dB时,系统可达到7径隐分集效果。
综上所述,实测曲线与理论曲线吻合,该隐分集分析方法可用于指导工程实践。
4 结束语
瑞利衰落信道中,采用扩频信号的DAR凭借其抗干扰、频谱复用、隐分集增益显著以及系统简单等优点,应用十分广泛,但其隐分集性能分析较为复杂,迄今未见通用公式。提出的隐分集增益分析方法既考虑了多重分集、多径数量对隐分集增益的影响,又考虑了多径强度对隐分集增益的影响,通用性很强,同时,实测结果也进一步验证了分析方法的准确性,对工程实践具有重要的指导意义。
[1]徐松毅,李文铎.瑞利衰落信道下非独立多重分集接收性能分析[J].电子学报,2003,31(11):1682-1685.
[2]中国人民解放军总参谋部通信部.对流层散射远距离通信[M].北京:中国人民解放军战士出版社,1982.
[3]刘丽哲.瑞利衰落信道下带内频率分集性能分析[J].无线电通信技术,2012,38(6):35 -37.
[4]张明高.对流层散射传播[M].北京:电子工业出版社2006.
[5]王斌.失真自适应接收机在散射信道中的应用[J].无线电工程,2005,35(7):3 -6.
[6]GOECKEL D.Performance of a Direct Sequence Spread Spectrum System with Rake Reception in a Multipath Fading Environment[C]//IEEE ISSSTA,1994:465 -469.
[7]WYSOCKI T A. Generalized Chirp Modulation Technique,Eur.Trans[J].Telecommun.Related Tech,1995,6(6):679 -683.
[8]张贤达,保铮.通信信号处理[M].北京:国防工业出版社,2000.
[9]KAASILA V P.Bit Error Probability of a Matched Filter in a Rayleigh Fading Multipath Channel,IEEE Trans[J].Commun,1994,42(234):826 -828.
[10]PROAKIS J G.数字通信 (第4版) [M].张力军,张宗橙,译.北京:电子工业出版社,2003.
[11]樊昌信,张甫翊,徐炳祥,等.通信原理[M].北京:国防工业出版社,2001:150-155.
