双回耦合输电线路的零序参数在线测量

梁志瑞，宫瑞邦，牛胜锁，赵 飞，张思为

（华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003）

0 引言

在电力系统中，需要测量线路的零序集中参数和零序分布参数。线路的零序集中参数表征的是线路的零序参数整体集中的效应，零序分布参数表征的是均匀分布在线路上的零序电气参数。目前，在很多地方由于线路走廊受限，同杆架设的线路日益增加，若采用传统离线测量方法，停电的影响范围将越来越广。因此，为了尽可能地避免因测量造成线路断电，通过尽量少次数的测量获得线路零序参数，提出了在线测量方法。

国内外针对输电线路零序参数在线测量的研究已进行了十几年。文献［1］在“一字形”零序集中参数电路模型的基础上提出了增量法，文献［2鄄4］介绍了增量法相关的硬件组成及测量过程，文献［5鄄7］在增量法的基础上提出了微分法、积分法等。“一字形”电路模型只考虑线间电磁耦合，忽略线路对地及线间的导纳，随着线路长度的增加及电压等级的升高，若不考虑线路的电容电流，使用该模型来测量计算会造成偏差。文献［8］对线路模型进行了改进，考虑了线路的对地零序导纳，通过建立零序分布参数和零序集中参数间的转换关系，将测量线路零序集中参数和测量零序分布参数结合起来。但是由于文献［8］所使用的线路模型没有考虑线间零序导纳的影响，而且对于线路参数矩阵的转换不够准确，最终未得到线路参数的精确测量算法。

本文针对双回耦合输电线路，综合考虑其线间电磁耦合和线路对地及线间电容的影响，建立它的零序分布参数电路模型和零序集中参数电路模型，推导零序集中参数与分布参数间的转换矩阵，研究其线路零序集中参数和分布参数的在线测量算法。

1.1 零序分布参数电路模型

1 双回耦合输电线路的零序电路模型

平行架设的双回耦合输电线路1、2参数完全一样，导线采取逆相序布置，沿线路近似采取一个全循环换位方式，线路参数沿线均匀分布。

根据零序电气量具有“大小相等、相位相同”的特征，对两回线进行解耦，最终可以用2根线路来代替原线路，构成两线-地的零序分布参数电路模型，如图1所示。记i回线路j端零序电压、零序电流相量分别为 Uij、Iij，j=1 时表示线路的首端，j=2 时表示线路末端。

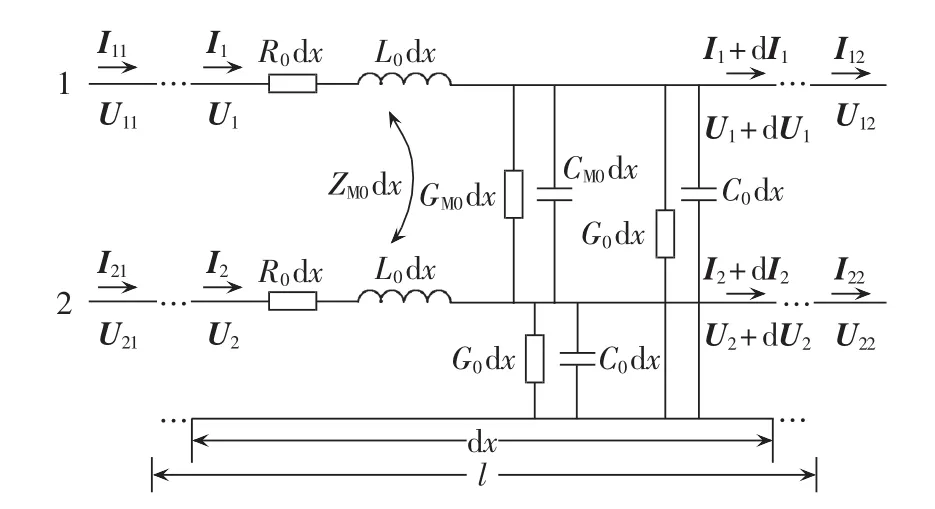
图1零序分布参数电路模型Fig.1 Circuit model with zero鄄sequence distributed parameters

图中，R0、L0为单位长度线路零序自电阻、自电感，ZM0为两回线间单位长度线路零序互阻抗，G0、C0为线与地之间单位长度线路的零序漏电导、零序电容，GM0、CM0为两回线间单位长度线路的零序漏电导、耦合电容，d x无限趋近于零，l为线路耦合段总长度。

记由 R0、L0、RM0、LM0构成的矩阵 Z0为线路的零序分布阻抗参数矩阵，由 G0、C0、GM0、CM0构成的矩阵Y0为线路的零序分布导纳参数矩阵。Z0、Y0分别为：

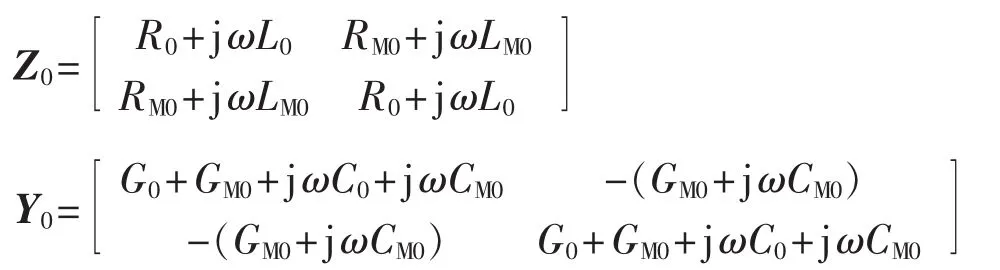
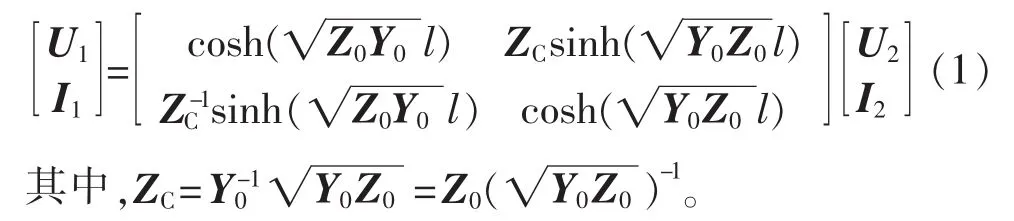
1.2 “双Π形”零序集中参数电路模型

根据电力系统分析的一般原理，当只关心线路两端的电气量时，可以将双回耦合线路等值为一个四端口的网络，进一步将其等值为“双Π形”零序集中参数电路模型，如图2所示。

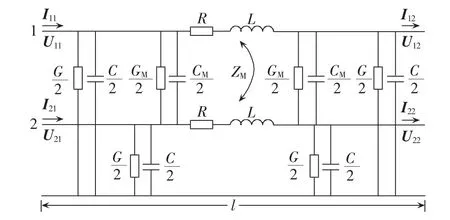
图2 “双Π形”零序集中参数电路模型Fig.2 Double-Π-shaped circuit model with zero-sequence lumped parameters

在此电路模型中，将线路总阻抗串联在线路上，将线路的总导纳等分为两部分，分别并联在线路的始、末端。图2中，R、L为线路零序集中自电阻、自电感，ZM为两回线间零序集中互阻抗，G、C为线与地之间的零序集中漏电导、零序电容，GM、CM为两回线间零序集中漏电导、耦合电容。

记由 R、L、RM、LM构成的矩阵 ZΠ为线路的零序集中阻抗参数矩阵，由G、C、GM、CM构成的矩阵YΠ为线路的零序集中导纳参数矩阵。ZΠ、YΠ分别为：

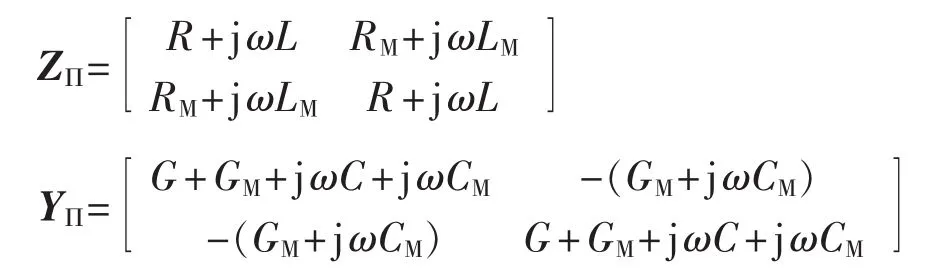
“双Π形”零序集中参数模型的网络传输方程如式（2）所示。

1.3 2种电路模型的转换

零序分布参数电路模型和“双Π形”零序集中参数电路模型是针对同一系统的不同表示形式，所以二者是等价的，因而2个电路模型的网络传输函数相等。根据式（1）和式（2），可以求出2种电路模型相应参数矩阵间的转换关系，如式（3）所示。

为讨论线路零序参数的分布特性与线路长度间的关系，进一步将式（3）变形为式（4）。式（4）中kZ、kY分别表示由Z0、Y0构成的转换矩阵。可以证得，当l趋于 0时，kZ、kY趋近于单位阵I。

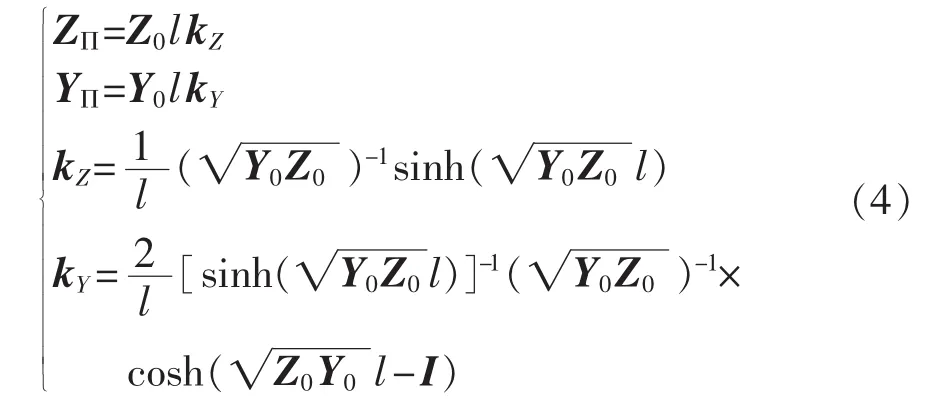
因此在线路长度较短时，双回耦合输电线零序参数的分布特性可以忽略，线路的零序集中参数可以近似等于零序分布参数与线路长度的乘积。当线路较长时，必须考虑分布特性。

2 双回耦合输电线路零序参数在线测量原理

输电线路零序参数在线测量是指在尽可能减少系统停电的前提下，测量线路两端的零序电压、电流，通过求解由线路参数、线路两端零序电气量构成的方程，获得输电线路的零序参数。

电力系统在正常运行时，线路两端的零序电压、电流很小，不能满足测量要求。因此，就需要通过改变运行状态，在线产生较大的零序增量，求解由线路参数、线路两端零序电气增量构成的方程，获得输电线路的零序参数。为保证准确地测量线路两端的零序增量，需要满足2个条件：一是在线产生足够大的零序增量；二是需同步测量线路两端的电气量。目前，多篇文献[9-14]描述了在线产生零序增量的方法，诸如将系统的运行方式从正常运行变为首端断相、末端接不平衡负荷、区外单相接地短路和区外双相接地短路等；线路两端电气量同步测量主要通过日渐成熟的基于GPS同步测量技术实现。

2.1 增量法原理

在改变系统运行方式后，会产生零序增量，记ΔU11、ΔU21、ΔU12、ΔU22、ΔI11、ΔI21、ΔI12、ΔI22为线路首末两端产生的零序电压、电流增量，ΔU1=[ΔU11，ΔU21]T，ΔU2=[ΔU12，ΔU22]T，ΔI1=[ΔI11，ΔI21]T，ΔI2=[ΔI12，ΔI22]T。

根据图2所示的“双Π形”零序集中参数模型，由式（2）推导出系统的伏安特性方程如式（5）所示。

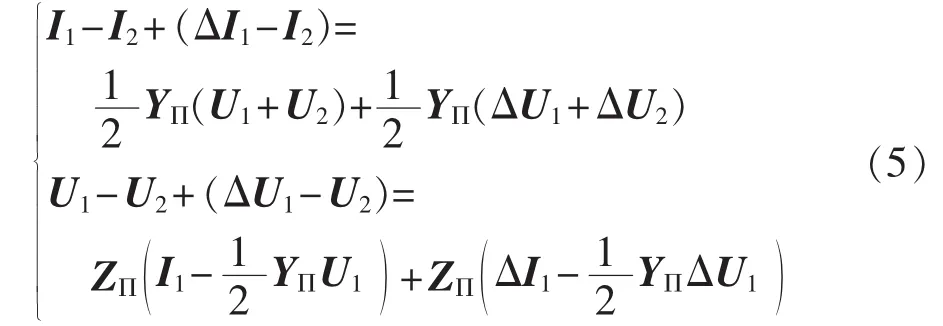
一般情况下，输电线路是一个线性系统，满足叠加原理。因此，式（5）可以认为是正常运行状态和零序增量的叠加。最终，基于线路首末端零序增量的增量方程如式（6）所示。

2.2 零序集中参数测量算法

线路的零序集中阻抗参数矩阵ZΠ的对角元素相等，非对角元素相等，同理于零序集中导纳参数矩阵YΠ。令2个矩阵的对角元素为Z、Y，非对角元素为ZM、YM。对式（6）所示的增量方程进行等价变形，得到用矩阵相乘形式表示的新增量方程，如式（7）、（8）所示。

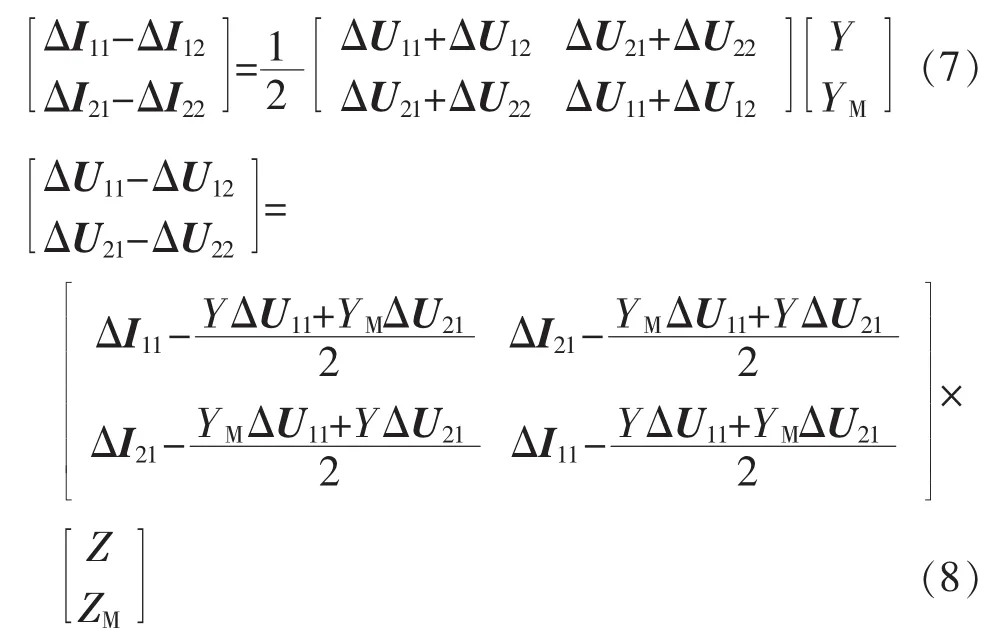
根据式（7），零序集中导纳参数矩阵YΠ中的对角元素Y和非对角元素YM的测量算法如式（9）所示。

将Y和YM代入式（8）中，得到Z及ZM。Z和ZM的表达式比较复杂，由于篇幅限制就不再列出，其测算原理与导纳的测算原理一致。经过上述一系列的工作，最终得到矩阵 ZΠ、YΠ。

零序集中参数的测量算法如式（10）所示。

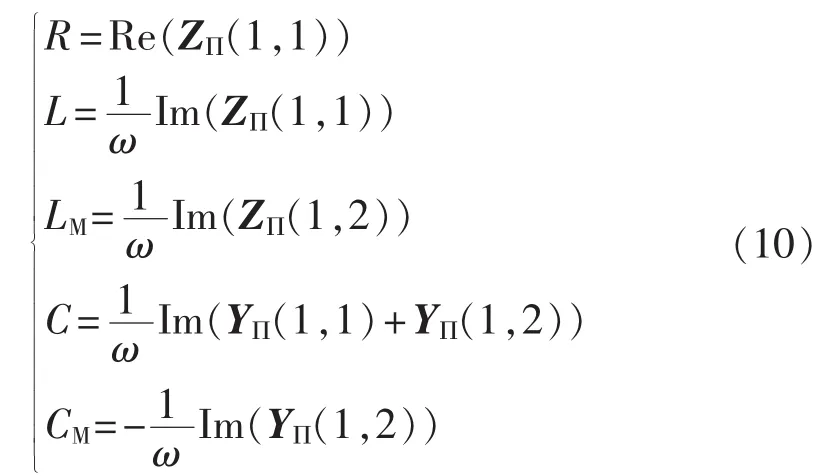
2.3 零序分布参数测量算法

在分布参数电路模型中，由于电阻、电感、电容和电导这些参数是均匀分布在线上的，因此必须用单位长度的输电线所具有的参数表示[15]。统称单位长度的输电线上具有的零序参数为线路的零序分布参数，在电力系统中，单位长度通常取1 km。

2.3.1 短线路零序分布参数测量算法

在线路长度较短时，对式（4）分析可知，“双Π形”集中参数电路模型与零序分布参数模型的转换矩阵kZ、kY近似于单位阵I。因此在测算短距离线路的零序分布参数时，可以令kZ、kY等于I，忽略线路波过程的影响。

短线路零序分布参数的测量算法如式（11）所示。

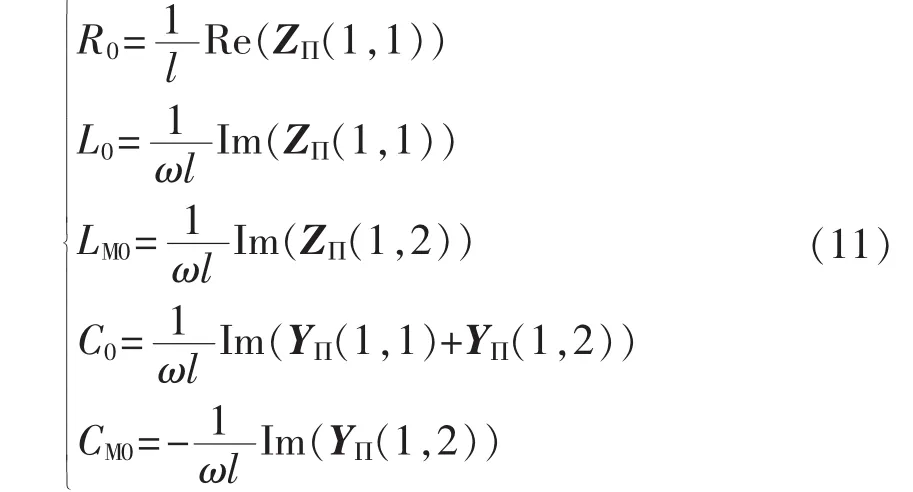
2.3.2 长线路零序分布参数测量算法

对于长距离输电线路，转换矩阵kZ、kY受线路长度的影响，已不能近似于单位阵I，需要对零序集中参数矩阵进行准确修正。根据式（3），将分布参数矩阵 Z0、Y0用 ZΠ、YΠ表示，如式（12）所示。

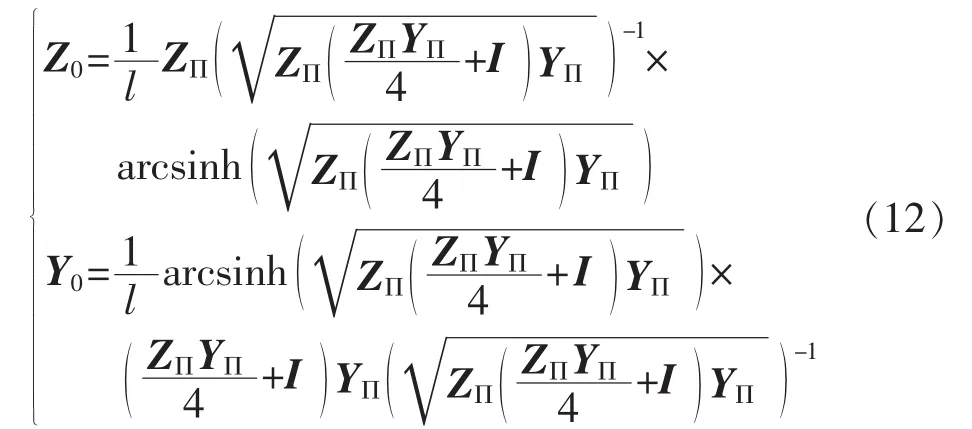
在测得线路的零序集中参数矩阵ZΠ、YΠ后，代入式（12）测算分布参数矩阵Z0、Y0。最后，长距离输电线路零序分布参数的测量算法如式（13）所示。

3 仿真及分析

为讨论本文所提耦合输电线路零序参数在线测量算法的准确性，在MATLAB中建立双回500kV线路系统，进行数字仿真。以三峡电站的出线为例[16]，导线型号为LGJ-630／55×4，分裂导线的分裂间距为450 mm，避雷线型号为 LHAGJ-150／25，杆塔为S1型，500kV双回耦合输电线路元件模块分布参数如下：R0=0.045 44 Ω／km；L0=1.551 9 mH／km；LM0=0.53105mH／km；C0=5.658nF／km；CM0=2.7894nF／km。

本文将仿真5种能产生零序电流增量的运行方式，即离线注入零序电流、首端断相、末端接不平衡负荷、区外单相接地短路和区外双相接地短路等，其中离线注入零序电流属于离线测量方法。

基于短线路零序分布参数测量算法在断开一回线路A相运行方式下的测量结果及误差如表1所示。基于长线路零序分布参数测量算法在断开一回线路A相运行方式下的测量结果及误差如表2所示。其他4种运行方式的仿真结果及误差的变化规律与表1及表2中的一致，限于篇幅，此处不再列出。

从表1可以看出，线路长度小于100 km时，仿真结果的误差较小，随着线路长度增加，误差增大。从表2可以看出，5条不同长度线路的仿真结果的误差都很小，除电阻外其他参数误差的数量级都为10-4。综合对比表1和表2，仅线路长度为60 km时，两表仿真结果的误差相近。

表1 基于短线路零序分布参数测量算法的仿真结果及误差Tab.1 Simulative results and error of measuring algorithm for zero-sequence distributed parameter of short line

表2 基于长线路零序分布参数测量算法的仿真结果及误差Tab.2 Simulative results and error of measuring algorithm for zero-sequence distributed parameter of long line

在实际中，当线路长度较短时，线路参数的分布特性可能没有仿真模型中的理想，应用中长线路零序分布参数测量算法测量短距离线路的零序参数可能会有较大的误差。因此，综合仿真结果，短线路零序分布参数测量算法适用于测量长度小于60 km的500kV线路，长线路零序分布参数测量算法适用于测量长度大于60 km的500kV线路。

此外，从表2中可以看出，线路长度小于150 km时，线路零序自电阻的测量误差相比其他参数略大，约为2%。这是由于线路零序自电阻要比电抗小一个数量级，在仿真中会有截断误差，因此不以电阻值的测量误差作为判断算法准确性的标准。随着线路长度逐渐增加，由数量级差异造成的截断误差会减小，如表2中当线路长度为500 km时，误差的绝对值已经减小到0.057%，可以证明这一点。

4 结论

本文建立了双回耦合输电线路的零序分布参数电路模型和“双Π形”零序集中参数电路模型，推导了零序集中参数与零序分布参数间的转换关系，提出了短线路零序分布参数在线测量算法和长线路零序分布参数在线测量算法，并进行了仿真验证。仿真结果表明，短线路零序分布参数测量算法适用于测量长度小于60 km的线路，长线路零序分布参数测量算法适用于测量长度大于60 km的中长距离线路，实验结果误差的数量级为10-4。本文提出的“双Π形”零序集中参数模型考虑了对地导纳和线间导纳影响，将输电线路零序集中参数在线测量与分布参数在线测量结合起来，可以为电力系统潮流计算和继电保护提供参考。