基于超级电容储能系统的动态电压恢复器研究

易桂平，胡仁杰

（东南大学 电气工程学院，江苏 南京 210096）

0 引言

近年来，电能质量问题越来越受到人们的关注，用户对供电质量的要求也越来越高。电能质量的异常通常表现为幅值或波形的异常，如电压暂降、三相不平衡、电压波动与闪变、谐波及频率变动等。其中电压暂降是目前最为普遍、危害最大的动态电能质量问题，抑制电压暂降的装置主要有并联型的配电静止无功补偿器（D-STATCOM）及串联型的动态电压恢复器（DVR）［1-2］。这些补偿装置可以补偿无功功率，但不能补偿有功功率，补偿性能易受到限制。

目前普遍采用的储能技术有电池、燃料电池、飞轮储能、超导储能等，其中电池储能历史悠久、技术成熟稳定、应用也相当地广泛，但存在工作环境要求高、运行维护复杂、使用寿命短等缺点。超级电容器是近几年来出现的一种新型储能技术，与电池储能相比具有许多显著的优势，因其具有循环使用寿命长、功率密度高、响应时间快、充放电效率高、控制简单和无污染等众多优点而被广泛地应用于大功率短期的充放电场合下。在电网电压波动的情况下，超级储能电容器可通过释放或吸收负荷端的有功功率来改善其电压质量。

本文对采用超级电容储能元件的DVR进行了分析，建立了基于等效电路的超级电容储能系统模型，提出了双向DC/DC变换器和双向DC/AC变换器的相关控制策略，仿真实验结果验证了该恢复器拓扑结构及其控制策略的有效性和正确性。

1 DVR对电压暂降的补偿分析

超级电容器储能 DVR的主电路如图1所示［3-4］，其主要由超级电容器组、电压型双向DC/DC变换器、电压型双向DC/AC变换器和控制装置组成。

当电网电压Us发生暂降时，DVR通过变压器串联在电路中，同时产生补偿电压UDVR来保持负荷端电压UL的幅值不变。由图1可得：

图1 超级电容器储能动态电压恢复器的主电路Fig.1 Main circuit of DVR based on SCES

设 UL的幅角为 0°，则将式（1）展开后得：

其中，Us、UDVR、UL、IL分别为 Us、UDVR、UL、IL的幅值；Zs为线路阻抗；α为UDVR的幅角；β为Zs的幅角；δ为Us的幅角；φ=arctan（QL/PL）。则 DVR 的容量为：

根据式（3）可画出DVR的对应相量图，如图2所示。

图2 DVR的相量图Fig.2 Phasor diagram of DVR

此DVR所补偿的电压幅值大小为：

在负荷电流给定的条件下，要使得DVR的容量最小，电压应取最小值，此时应该满足：

求解式（6）得：

则依据已知条件可以计算出Us的幅角δ值，再将得出的δ值分别代入式（3）和式（4），就可得到串联型DVR的最小容量和最小注入电压。

假设没有超级电容器储能单元，DVR只补偿无功功率，则此时应该满足：

代入式（3）可得：

要满足等式（9），就必须同时满足如下不等式：

从以上分析可以看出采用纯无功方式不一定能补偿电压暂降，因此，补偿方案应将逆变器等主回路装置的容量和储能系统的容量有机地结合起来，采用超级电容作为DVR储能单元，可在经济和技术上都获得比较合理的方案［5-8］。当电源电压发生暂降时，储能单元经升压逆变器输出有功功率；当电源电压出现骤升时，储能单元吸收整流器降压后的有功功率，来维持负荷电压的稳定。

2 DVR的数学模型

2.1 双向DC/DC变换器的数学模型

本文采用的非隔离型Buck-Boost双向DC/DC变换器结构见图 3［9-11］。

图3 非隔离型Buck-Boost双向DC/DC变换器Fig.3 Non-isolated bi-directional Buck-Boost DC/DC converter

设VT1的导通时间为d，以理想电容电压uC和电感电流iL作为状态变量，采用状态空间平均法，建立相应的状态方程如下：

则在稳态工作点（uC0，iL0，iload0，d0，us0）处有：

在稳态工作点处施加扰动：uC=uC0+ΔuC，us=us0+Δus，iload=iload0+Δiload，iL=iL0+ΔiL，d=d0+Δd，忽略二阶分量，线性化后可得到相应的小信号模型：

取电容电压uC、电感电流iL与输出电流io为输出量，则可得系统的输出方程：

线性化后可得：

由式（13）和式（15）建立 Buck-Boost双向变换器，系统框图如图 4 所示［7］。

图4 Buck-Boost双向变换器系统框图Fig.4 Block diagram of bi-directional Buck-Boost converter system

2.2 双向DC/AC变换器的数学模型

双向DC/AC变换器主电路结构如图5所示［7-14］，直流电压Ud经过PWM电路后产生逆变桥的输出电压Ui，Ui通过二阶LC滤波器得到正弦波输出电压UC′，即 DC/AC变换器的输出，L′和 r分别为滤波电感及其等效阻抗，C′为滤波电容。

图5 双向DC/AC变换器主电路Fig.5 Main circuit of bi-directional DC/AC converter

对于图5的全桥DC/AC变换器，忽略逆变桥的滞后作用，将其看作比例环节，根据LC滤波器可以写出以［UC′，IL′］T为状态变量的状态方程：

其中，UC′为电容电压，IL′为电感电流，Ui为逆变桥输出电压，其值为：

其中，S*是开关函数，当 VTl、VT4管导通，VT2、VT3管关断时，S*=1；反之，S*=0。

2.C 提示:A项,铜与浓硝酸、稀硝酸反应的产物不同;B项,钠与氧气在常温条件下的反应和在加热条件下反应的产物不同;C项,氢气与氯气无论是加热还是点燃条件下的产物都是HCl,不受反应物用量、条件、反应物浓度的影响;D项,氯化铝与少量氢氧化钠溶液反应生成氢氧化铝,与足量氢氧化钠溶液反应生成偏铝酸钠,产物不同。

显然，由于开关器件具有开通和关断2种状态，导致方程非线性，但是在2种状态期间，方程又是线性的，所以可以用分段线性化来进行系统建模。这种方法在数字控制中应用十分广泛，而且利用计算机的数值计算功能可以对系统进行仿真，它可以精确地模拟电路的工作过程，借助可视化软件可以对结果做出直观的分析。但是，在某些场合，尤其是频域分析中，分段线性化会使主电路的传递函数复杂化，增加系统分析和设计的难度。因此，系统建模通常采用状态空间平均法，它是基于输出频率与响应频率远小于开关频率的情况，在一个开关周期内，用变量的平均值代替其瞬时值，从而得到连续状态空间平均模型。在此基础上，运用小信号分析法，可以非常方便地使用频域分析的各种工具。

当SPWM是线性调制时，输出脉宽与参考正弦波幅值成正比，将开关函数用近似表示为：

其中，D为占空比；UM为三角载波峰值；Ur为调制波幅值。

令调制度 M=Ur/UM，并将式（18）代入式（17）后得到：

将式（19）代入式（16）得到：

式（20）就是利用状态空间平均法建立的状态空间平均模型，可以推出其频域传递函数：

可见系统近似为一个二阶振荡环节，尤其是在空载状态下，由于等效电阻r很小，系统近似为无阻尼振荡环节，对扰动的抑制能力很弱。

图6 双向DC/AC变换器的数学模型框图Fig.6 Mathematical model of bi-directional DC/AC converter

3 DVR的控制策略

3.1 双向DC/DC变换器的控制策略

已有研究表明，在恒定功率负载条件下，由于恒定功率负载的负阻特性，使得控制系统存在正极点，所以开环不稳定，并且为非最小的相位系统。同时，Buck-Boost双向变换器为二阶非线性仿射系统，即使在某一稳态点处对其进行线性化，也可能失去大信号稳定性；且参考输入或者输出功率变化的动态过程体现了非线性，不宜用线性模型表示。因此，为了保证Buck-Boost双向变换器在各种负载条件下，尤其是恒功率负载条件下的静态、动态特性，根据本文串级控制的思想以及稳定直流侧电压的控制目标，可以采用电感电流和电容电压状态双闭环反馈控制，控制系统框图如图 7所示［14-16］。

图7 控制系统框图Fig.7 Block diagram of control system

由图4和图7可建立电流的内环传递函数：

其中，D0为稳态占空比，其值在（0，1）范围内。如果不考虑控制系统的延时，电流内环则可表示成增益为K的比例环节。而对于电容电压外环，采用恒压控制时有ΔuC_ref=0，则可建立电压外环传递函数：

由式（23）可知，Δus和 Δiload的变化将引起母线电压的波动ΔuC。为了减少母线电压的波动，一是可以增大母线的电容，但会使得系统的体积增大，同时也会减缓系统的响应速度；二是通过加强控制器GVR（s）的作用，但是如果负荷波动较大，短时间内仍然会引起母线的电压波动。为了抑制Δus和Δiload的变化对母线电压的影响，可以引入功率前馈的方法，其系统控制框图如图8所示。

由图8可建立电压外环传递函数：

结合式（12），由式（25）可知，如果忽略电源损耗rs及电感，取Kf=1/K则可完全消除Δus和Δiload带来的影响，即理论上直流母线电压不再受电源电压和负荷电流的影响，暂态情况下仍然保持稳定。

图8 带功率前馈的系统控制框图Fig.8 Block diagram of system control with power feed-forward

3.2 双向DC/AC变换器的控制策略

电压相位一般通过锁相环（PLL）来监测，假定同步旋转坐标系d轴的方向和a相电压的方向一致，根据abc/dq坐标变换可求得负荷电压的d轴和q轴分量：

其中，uf为负荷额定电压的标幺值；ufd和ufq分别为负荷电压d轴和q轴分量的标幺值。根据负荷变化和电源电压可得到负荷电压的d轴和q轴参考值：

其中，Pf为负荷额定功率的标幺值；ufd，ref为负荷电压d轴分量的参考值；ufq，ref为负荷电压q轴分量的参考值。

为了通过实现解耦控制来提高DVR的响应速度，本文采用前馈补偿的PI反馈控制法来控制此DVR，控制原理如图9所示。图中，ufa、ufb和ufc为负荷相电压；usa、usb和 usc为电源相电压；ia、ib和 ic为双向DC/AC变换器交流侧的输入电流［16-19］。

图9 双向DC/AC变换器控制框图Fig.9 Block diagram of bi-directional DC/AC converter control

实现控制策略的关键是如何选择滤波器。为滤除经过同步旋转坐标变换后的电流和电压的负序分量，本文采用陷波低通滤波器，此种滤波器的响应速度较快。当负荷电压信号变化时，控制信号Δufd和Δufq分别通过比例积分（PI）环节产生电流控制信号id，ref和 iq，ref，采用解耦前馈控制得到电压控制量 urd和urq后，再经过dq/abc坐标变换成参考电压ura、urb和urc，最后将其输入到SPWM调制器中。

4 系统仿真实验

基于PSCAD/EMTDC软件平台对所设计的DVR进行了仿真分析。电源功率因数为0.99；供电频率为50 Hz；负荷的线电压额定值为0.4 kV，额定功率为15kW；负载为三相对称电阻。超级电容器采用ESMA公司30EC402U模块，单个电容器模块电压为45 V、电容为330 F、等效串联电阻为9 mΩ、最大功率为20 kW，超级电容器组由上述4个模块串联而成。在0.2～0.3 s，a、b、c三相分别发生 10%、50% 的电压暂降和电压中断，仿真结果如下。

a.a、b、c三相同时发生10%的电压暂降。仿真波形如图10、11所示。

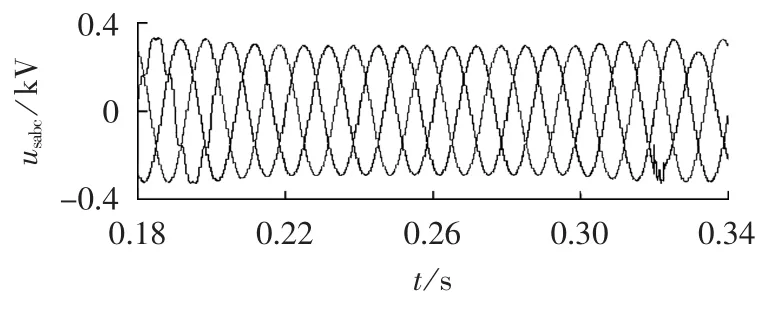
图10 发生10%电压暂降时的三相电压波形Fig.10 Three-phase voltage waveforms during 10%voltage sag

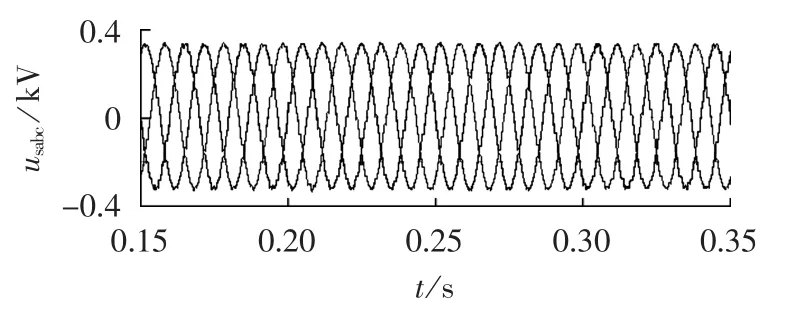
图11 补偿后的三相电压波形Fig.11 Three-phase voltage waveforms after compensation

b.a、b、c三相同时发生50%的电压暂降。仿真波形如图12—15所示。

c.a、b、c三相同时发生电压中断。仿真波形如图16、17 所示。

图12 发生50%电压暂降时的三相电压波形Fig.12 Three-phase voltage waveforms during 50%voltage sag

图13 补偿后的三相电压波形Fig.13 Three-phase voltage waveforms after compensation

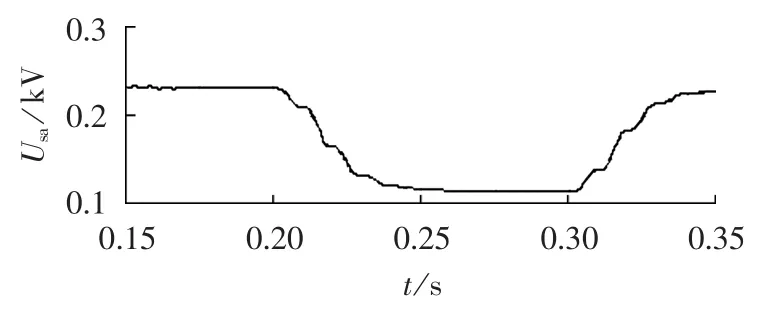
图14 补偿前a相电压有效值Fig.14 RMS value of phase-a voltage before compensation

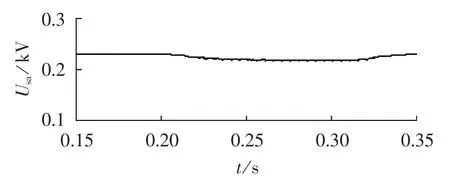
图15 补偿后a相电压有效值Fig.15 RMS value of phase-a voltage after compensation

图16 电压发生中断时的三相电压波形Fig.16 Three-phase voltage waveforms during voltage interrupt

图17 补偿后的三相电压波形Fig.17 Three-phase voltage waveforms after compensation

5 结论

本文对DVR的补偿特性进行了分析，可以看出无储能DVR补偿时电压幅值和电压相位无法完全兼顾，且补偿范围有限，补偿前后对负载的冲击较大。因此，为了达到比较好的补偿效果，利用超级电容器作为直流侧的储能单元，在电源电压发生暂降时可调节负荷电压，提高负荷电压的稳定性。仿真结果表明了本文所设计的DVR具有良好的动态补偿性能和负载适应性，同时也验证了其拓扑结构及控制策略的正确性和有效性。