基于多元非线性回归模型的环型中压配电网最大供电能力评估方法

吴云亮 ，沈阳武，林 超 ，彭晓涛 ，孙元章 ，许良柱

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.凯里供电局，贵州 凯里 556000）

0 引言

城市配电网作为联系终端用户与发、输电系统的重要纽带，是城市建设和经济发展的重要基础设施，担负着给终端用户提供安全、可靠、优质电能的关键职责［1］。科学合理地评估城市配电网的最大供电能力对于优化系统网架结构及指导城市电网的规划和运行具有巨大的经济价值和现实意义［1-3］。

目前计算配电网供电能力的方法主要有以最大最小负荷倍数法［4］、网络最大流法［5］和变压器容载比法［6］为代表的传统方法，数学优化方 法［7-8］及 基于N-1安全准则和主变互联的新方法［9-10］。传统方法虽然深入到变电站馈线层面评价配电网的供电能力，但是计算方法一般比较繁琐，在网络结构比较复杂的情况下不一定能得到准确的结果。数学优化方法着眼于建立配电网供电能力的优化模型，如文献［7］提出了一种求解配电网最大供电能力的线性规划模型。该方法基于直流潮流计算，以网络能供应的最大负荷为目标函数，虽然能够提高计算速度，但是忽略了母线电压幅值的变化以及线路的电阻。文献［8］提出一种基于信赖域法的城市电网最大供电能力计算方法。该方法基于交流潮流计算，以网络最大负荷供电能力为目标函数，并考虑了线路热稳定、变压器容量等约束条件。该方法需要在每一个搜索点采取参数摄动法对目标函数进行二阶等值，等值模型的精度对结果影响较大，并且计算的复杂度极大增加。由于上述方法［4-8］在计算过程中没有考虑到N-1供电安全准则，而城市电力规划设计导则中对规划电网具备任一线路停运或者变电站一台主变退出运行时仍能保证向用户持续供电的要求做出了明确规定［11-13］，因此出现了基于N-1供电安全准则和主变互联的新方法［9-10］。

上述研究的对象主要针对开环运行的配电网，而关于环型供电的城市中压配电网最大供电能力的研究却鲜有报道。基于这种考虑，本文提出了一种基于多元非线性回归模型的环型中压配电网最大供电能力评估方法。首先基于潮流跟踪理论确定线路功率的主导开闭所负荷，并建立线路功率与主导开闭所负荷之间的多元非线性回归模型。随后在此基础上，提出了以变电站下网功率之和最大为目标函数，以电网N-1供电安全准则下的变电站主变、线路传输容量限制及开闭所容量限制为约束条件的环型配电网最大供电能力求解模型，并利用序列二次规划算法获得该模型的全局最优解。最后，通过8节点环网算例和凯里城区2015年规划双环配电网算例验证了本文所提方法的可行性和有效性。

1 中压配电网环型供电网架结构

1.1 环型网架结构设计实例

本文以凯里城区2015年规划双环配电网（如图1所示）为例说明中压配电网的环型供电网架结构。从规划运行的角度讲，该结构的提出主要是为解决凯里城区由于线路通道及土地资源比较紧张，负荷中心不能新建变电站作为支撑电源，供电可靠性较低和线路负载率过高的问题。

由图1可见，该网架结构以110kV变电站为电源，由10 kV开闭所通过“手拉手”联络分别构成2个中压环型配电网络的主干网架。

变电站至开闭所及开闭所之间均采用双回电缆供电。2个环型主干网架上的开闭所由变电站直接供电，其中内环由3座110 kV变电站通过10个开闭所进行供电，外环由4座110 kV变电站通过16个开闭所进行供电。变电站与开闭所之间的馈线不带负荷，负荷经开闭所输出馈线直接供电。

图1 凯里2015年规划双环配电网结构Fig.1 Structure of 2015’planned double loop distribution network of Kaili

1.2 环型网架结构的特点

a.实现了分层分区供电。供电区域简明清晰化，便于实现配电网自动化，同时体现了电源深入负荷中心的原则。

b.供电可靠性极大提高。在内环或外环仅有一座110 kV变电站的情况下，环网仍然能为重要负荷进行不间断供电。

c.短路电流的限制问题。可采用减小输电网与配电网之间及其内部的电磁环网通路、110 kV变电站10 kV母线和开闭所10 kV母线联络分母运行、110 kV变电站10 kV侧安装限流电抗器等措施将短路电流限制在断路器的开断能力之内。

d.运行经济性问题。可利用全寿命周期成本分析法来评估闭环供电方式的长期经济效益。由于闭环运行短路电流的有效抑制，原配电网的保护设备大部分可再次利用，故主要的电网一次投资成本是由线路改造成本构成。同时由于供电质量和可靠性的提高，电网运行成本和故障引起的缺电成本都将大幅度下降，随着运行时间的增长，这部分成本下降所带来的经济效益会愈加明显。

因此，与常规的中压配电网不同，本文研究的环型网架模型能在大部分的时间内保持闭环供电方式。

2 线路功率分摊的多元非线性回归模型

2.1 潮流跟踪基本原理

潮流跟踪是指在潮流分布已经确定的情况下，确定负荷吸收的功率从哪些支路以多大的份额传送过来或支路的传输功率被哪些负荷以多大份额使用［14］。根据文献［15］，负荷对线路功率的汲取关系可由式（1）表示。

其中，Pst为任一线路s-t的传输功率；PLi-st为任一节点 i的负荷 PLi对 Pst的汲取；KLit为 PLi对 Pst的汲取系数，其具体计算方法可参见文献［15］。

2.2 负荷对线路功率汲取的多元非线性回归模型

对一个给定的电力网络，通过式（1）可以求得节点i的负荷对线路s-t汲取的有功功率PLi-st。由Weierstrass第一定理知［16］：任何函数都可用多项式以任意精度逼近，因此PLi-st可由PLi的r次多项式表示：

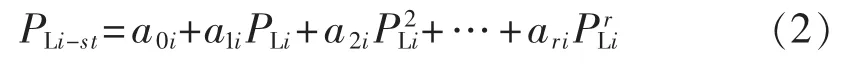
其中，a0i、a1i、a2i、…、ari为回归系数，可通过 r+1 组不同负荷分布情况构成的样本数据组（PLik-st，PLik）（k=1，2，…，r+1）求得。式（2）为节点 i的负荷对线路s-t汲取功率的非线性回归模型，其能够直观地反映出节点i的负荷对线路s-t汲取功率随自身负荷变化的定量关系。

实际电网中，节点i的负荷对线路s-t的汲取功率不仅与自身的大小相关，而且与电网中其他负荷的分布相关。因此为计及所有负荷对PLi-st的影响，本文提出了节点i的负荷对线路s-t汲取功率的多元非线性回归模型，如式（3）所示。

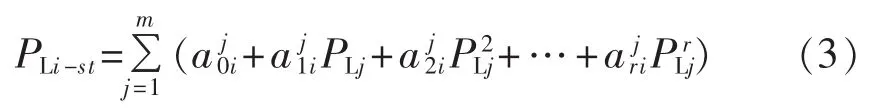
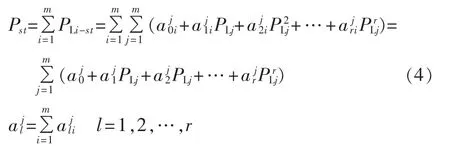
2.3 基于潮流跟踪理论的主导负荷选择

实际系统中不同负荷对Pst的影响各不相同，在建立式（4）的过程中可以剔除那些对Pst影响较小的负荷，只考虑对Pst影响较大的负荷，这样可以减少式（4）的复杂度，进而加快优化问题的求解速度。基于这种考虑，本文提出了负荷对线路功率的贡献因子指标以遴选对Pst影响较大的主导负荷。式（5）给出了贡献因子的计算公式。

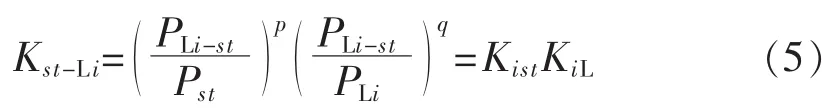
其中，Kist为节点i的负荷从线路s-t汲取的功率占总线路功率的比重，Kist越大，表明线路s-t供给节点i负荷的功率越多；KiL为节点i的负荷从线路s-t汲取的功率占自身负荷大小的比重，KiL越大，表明节点i的负荷从线路s-t汲取的功率越多；p和q为幂指数权重，主要根据经验进行选取，一般 p和 q的取值范围为0.8～1，本文取p=q=0.9。Kst-Li越大，表明节点i的负荷对Pst的影响越大。

考虑系统的多种负荷分布情况，Pst的主导负荷可以由 Kst-Li的均值来确定。的计算公式为：

2.4 多元非线性回归模型的修正

确定Pst的主导负荷后，在建立式（4）时只需计及主导负荷对Pst的影响。因此式（4）可修正为：

其中，Dst为Pst的主导负荷集合。回归系数通过主导开闭所不同负荷分布及相应负荷分布情况下线路s-t功率的样本数据组，由最小二乘原理得到的。通过改变系统中开闭所负荷大小，再由潮流计算得到每一组开闭所负荷分布情况下线路s-t的功率，即可得到主导开闭所负荷PLj与线路s-t功率Pst的多组样本数据。

根据式（7），即可直接由主导开闭所负荷求出配电网中所有线路的传输功率，而不需要在负荷改变时每次都重新进行潮流计算。需要说明的是：在环型供电中压配电网中，线路s-t既能代表变电站的供电出线，也能代表开闭所之间的联络线，因此变电站供电出线的下网功率和开闭所之间联络线的传输功率均可由式（7）表示。

3 环型供电中压配电网最大供电能力的评估模型

城市环型供电中压配电网的最大供电能力是指在满足各种可靠性和安全性约束的条件下，中压配电网所能供应的最大负荷。求解环型供电中压配电网最大供电能力的目标函数可定义为［7-8］：

在不考虑网络损耗的前提下，中压配电网中各节点的负荷之和等于变电站下网功率和配网中的电源出力之和，即：

其中，Dsub为变电站供电出线集合，Dg为配网电源集合。

通常情况下，对于配网中的电源，可以当作负的负荷进行处理，对于同一负荷节点上的电源和负荷，两者可以进行叠加，根据负荷的大小和电源的出力等效为一个正（负）的负荷。基于这种考虑，式（9）可以重写为：

其中，P′Li为等效后的负荷功率，m′为等效后的负荷节点数目。

由式（10）可知，环型供电中压配电网的最大供电能力可以等效为变电站下网功率的最大值，即：

系统运行的约束条件包括电网N-1供电安全准则下的变电站主变、线路传输容量约束及开闭所容量约束。

为了计及配电网N-1供电安全准则，变电站主变和线路传输容量必须满足一定条件，即：

其中，Simax、Simin分别为变电站主变容量的上、下限；Pstmax、Pstmin为线路s-t传输容量的上、下限。本文考虑线路在正常运行状态下的传输容量上限按其额定传输容量的50%来确定。

开闭所容量决定了该节点可带负荷范围，即：

其中，P′Limax、P′Limin分别表示节点i等效负荷的上、下限。

4 基于序列二次规划算法的模型求解流程

式（11）—（13）所示的最大供电能力模型是一个带约束的高维非线性优化问题，考虑到序列二次规划算法的超线性收敛速度、全局收敛性和高效处理不等式约束的优势［17］，本文采用序列二次规划算法实现环型供电中压配电网的最大供电能力的求解。具体步骤如下：

a.确定配电网网架结构、线路和负荷等参数，形成基础数据库和网络拓扑图；

b.采用蒙特卡洛数值摄动法［8］，确定配电网中各开闭所的若干组负荷分布值；

c.针对步骤b中确定的不同负荷分布情况分别进行潮流计算，在此基础上由式（1）确定各开闭所负荷对线路功率的汲取情况；

d.通过式（5）和式（6）确定线路的主导开闭所，并建立式（7）所示的线路功率与主导开闭所负荷的多元非线性回归模型；

e.建立如式（11）—（13）所示的环型供电中压配电网最大供电能力模型；

f.采用序列二次规划算法对最大供电能力模型进行求解。

5 算例分析

为了验证本文所提方法的正确性和有效性，以8节点环型配电网算例和凯里城区2015年规划双环配电网为例分别计算其最大供电能力。

5.1 8节点环型配电网算例

8节点环型配电网的结构如图2所示。该环型配电网由6个10 kV开闭所组成环网，环网通过2个110 kV变电站进行供电。开闭所与开闭所之间及变电站与开闭所之间都由双回线路相连。

图2 8节点环型配电网结构图Fig.2 Structure of an 8-bus loop distribution network

表1给出了各开闭所负荷的初值和分布范围。在开闭所负荷为初值的情况下，各开闭所负荷对线路a—f功率的汲取情况如表2所示。

表1 开闭所负荷初值及分布范围Tab.1 Initial value and range of switching station loads

表2 开闭所负荷对线路功率的汲取Tab.2 Extracted power of switching station load from transmission line

对照表2，以线路b为例，可知其功率5.7475MW分别分配给开闭所1为0.2728 MW，分配给开闭所2为5.4747 MW；同时以开闭所4为例，可知其分别从线路c、d汲取功率0.6547 MW、7.9453 MW。

在每个开闭所的负荷范围内，通过蒙特卡洛法模拟开闭所的负荷变化，分别由式（1）计算各开闭所负荷对线路功率的汲取情况，并通过式（5）和式（6）确定线路功率的主导开闭所负荷，结果如表3所示。

表3 最大供电能力下的开闭所负荷Tab.3 Switching station loads under maximum power supply capability

图3中线路功率为标幺值，由图3可知，由多元非线性回归模型求出的线路功率值与潮流计算的结果基本一致的，最大误差为3%，说明本文采用的多元非线性回归模型能准确反映出电网的实际运行状况。当电网中的负荷分布已知时，能够通过多元非线性回归模型经过简单的多项式计算获得线路传输功率的大小，而不需要进行潮流计算。

图3 回归模型与潮流计算对比结果Fig.3 Comparison of results between regression model and power flow calculation

在确定了线路功率与开闭所负荷之间的多元非线性回归模型之后，采用序列二次规划方法求解式（11）—（13）所示的最大供电能力目标函数，可得环型供电中压配电网的最大供电能力为45.9 MW。表4给出了中压配电网在最大供电能力情况下开闭所至变电站线路的下网功率。

表4 最大供电能力下的开闭所至变电站线路下网功率Tab.4 Transmission line power transferred from switching stations to substations under maximum power supply capability

5.2 凯里城区2015年规划双环配电网算例

针对如图1所示的凯里城区2015年规划双环配电网，按照第4节的步骤求解其最大供电能力，结果如表5、6所示。

由表5知，图1所示的凯里城区2015年规划双环配电网最大供电能力为205.75MW，大于其2015年负荷预测值178 MW。由表6可知，在最大供电能力对应的开闭所负荷情况下，变电站至开闭所的线路功率基本接近其N-1准则下的稳定极限（双回线路的稳定极限为8MW），即线路负载率得到了最大限度的利用。将表5对应的最大供电能力下的开闭所负荷代入到电力系统仿真综合程序PSASP中进行N-1潮流计算校核可知，断开电网中的任一条线路，其他线路或变压器均未出现过载现象；同时在此负荷水平下，任一开闭所负荷的少量增加都会造成N-1校验时某些线路功率超过其容量限值，由此可证明利用本文方法求取环型供电中压配电网的最大供电能力是有效的。算例网络的供电能力评估经过6次迭代之后目标函数即收敛，寻优程序的运行时间很短。

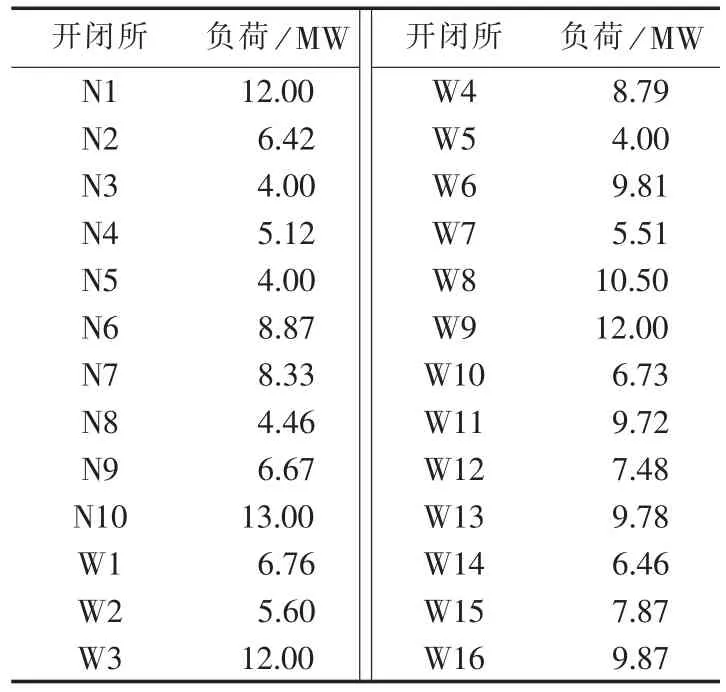
表5 最大供电能力下的开闭所负荷Tab.5 Switching station loads under maximum power supply capability

表7给出了分别采用序列二次规划算法、粒子群算法及遗传算法求解最大供电能力的结果及程序的运行时间。

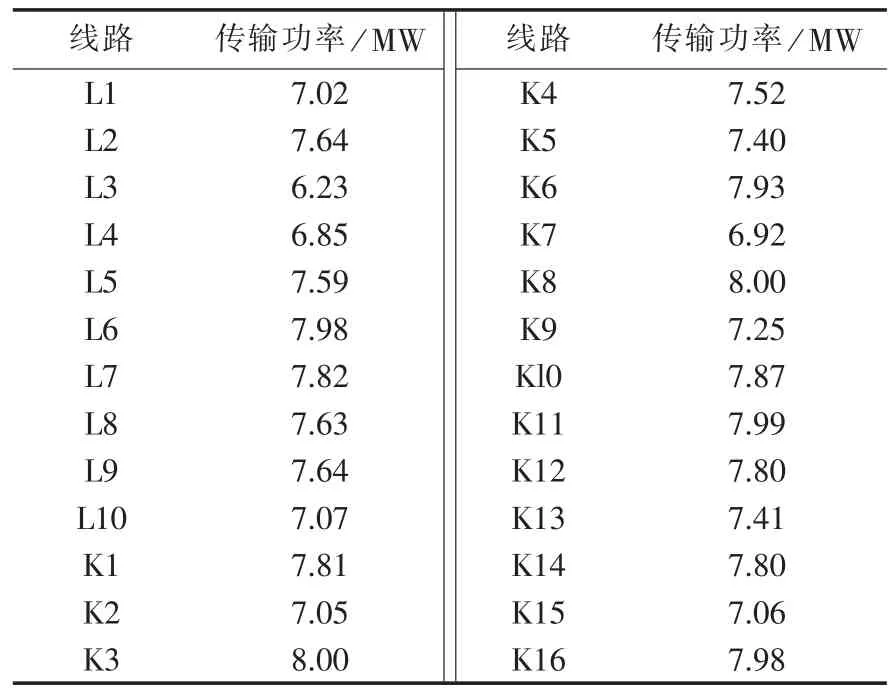
表6 最大供电能力下的变电站至开闭所线路下网功率Tab.6 Transmission line power transferred from substations to switching stations under maximum power supply capability

表7 不同求解算法的结果比较Tab.7 Comparison of results among different algorithms

由表7可知，采用序列二次规划算法得到的最大供电能力比粒子群算法和遗传算法的结果大。其主要原因在于本文提出的最大供电能力模型以变电站至开闭所线路的有功功率之和最大为目标函数，包含了网络中的有功损耗部分。同时采用的序列二次规划算法由于具有全局收敛的特点，因此能够获得目标函数的全局最优解，而演化类的粒子群算法和遗传算法由于具有随机性，每次求解结果不确定，往往比较难以获得目标函数的全局最优解。

6 结论

本文首先介绍了中压配电网环型供电网架结构特点，然后提出了一种基于多元非线性回归模型的环型中压配电网最大供电能力求解模型，最后针对2个实际系统算例利用序列二次规划算法获得了该模型的最优解。本文所提方法不仅计及了电网N-1供电安全准则的要求，同时能够避免优化模型求解过程中的潮流计算。仿真结果表明：本文所提的最大供电能力求解模型是可行和有效的，采用序列二次规划算法进行寻优，最优解收敛迅速，计算时间短。本文的研究结果可为城市环型中压配电网的规划和运行提供一定的参考依据。