基于偏最小二乘法评价低渗透砂岩储层质量

胡作维，李 云

(油气藏地质及开发工程国家重点实验室 成都理工大学，四川 成都 610059)

引 言

低渗透油气资源在中国油气勘探开发中具有重要的战略地位，近年中国低渗透油气产量所占比例持续增大，未来中国实现油气产量稳产、增产必将更多地依靠低渗透油气的高效勘探开发［1］。中国低渗透油气藏具有含油气层系多、油气藏类型多、分布区域广等特点，是导致目前中国低渗透油气勘探开发中存在诸多难点的重要原因。尽管低渗透油气藏的形成与很多地质因素有关，但微观孔隙结构对低渗透砂岩储层质量的直接控制作用越来越为大家所认同，因而近年来孔隙结构分析在低渗透砂岩储层评价工作中的重要意义越来越得到大家的重视［2－4］。然而，与孔隙结构有关的参数众多，难以确定哪些参数更能直接表征低渗透砂岩储层质量的好差。为此，本文应用偏最小二乘法评价不同孔隙结构参数对低渗透砂岩储层质量的表征能力。

1 计算结果

偏最小二乘法(Partial Least Squares，简称“PLS”)由 Wold［5］等在 1983 年首次提出，是一种多因变量对多自变量的多元统计数据分析方法，能够将主成分分析、典型相关及多元线性回归分析有机地结合起来，尤其适用于变量多重相关性、小样本等情况下多对多线性回归分析［6－7］。

在实际计算过程中，本文采用了鄂尔多斯盆地姬塬地区长2油层组低渗透砂岩储层52组实际数据，将储层质量评价参数——孔隙度(%)y1、渗透率(10－3μm2)y2作为因变量，孔隙结构参数——排驱压力(MPa)x1、中值压力(MPa)x2、最大汞饱和度(%)x3、孔喉均值x4、分选系数 x5、变异系数 x6、歪度x7、结构系数x8作为自变量;同时，为了保证偏最小二乘回归模型具有更高的合理性和精确性，本文依据主成分判别椭圆方法剔除特异数据点，以及根据交叉有效性(Q2)原则(Q2≥0.0975)判断某个主成分的引入是否对回归模型预测能力具有明显的贡献作用［7］。

在偏最小二乘回归计算过程中，最终剔除了分布在判别椭圆外的11个特异样本点;同时，当孔隙度回归模型提取到第6个主成分t6时，Q2＜0.0975，因而只需提取5个主成分即可满足模型的精度要求(表1);当渗透率回归模型提取到第6个主成分t6时，Q2＞0.0975，但第6个主成分t6对因变量y2的解释能力并没有进一步提升，因而同样只需提取5个主成分即可满足模型的精度要求(表1)，最终偏最小二乘回归分析获得了孔隙结构对低渗透砂岩储层质量影响的标准化回归方程，计算结果如表 1所示。

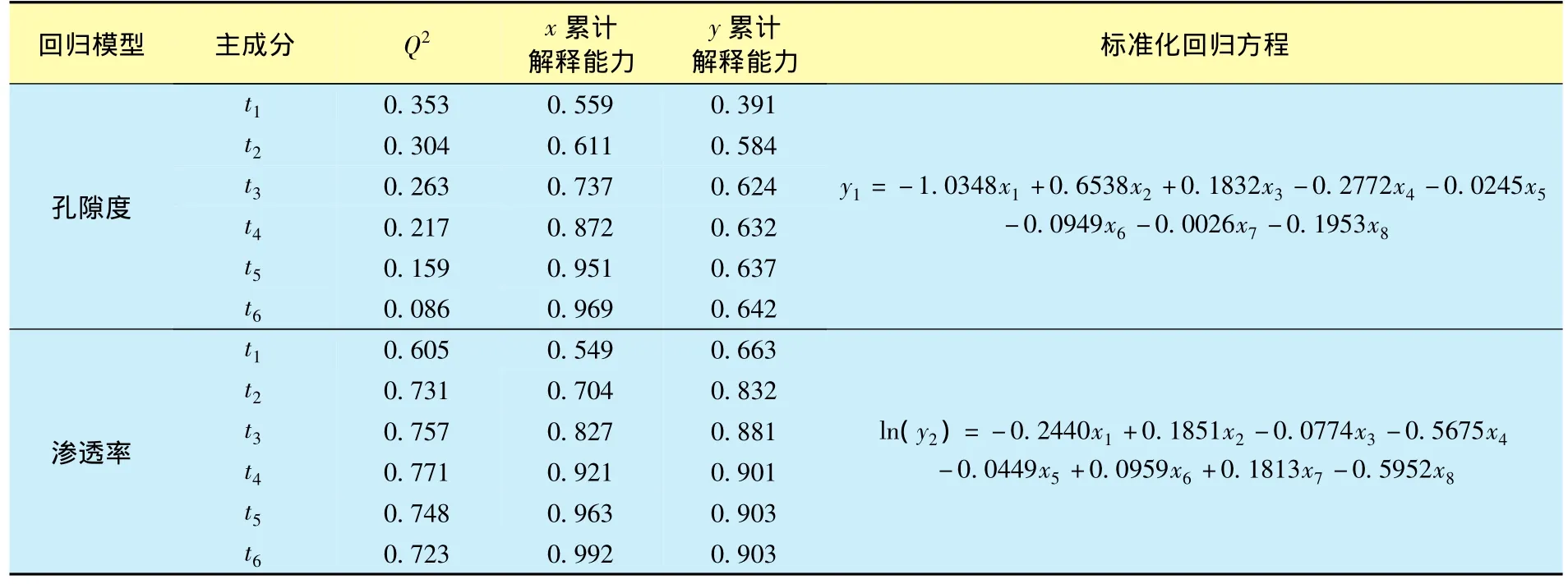
表1 偏最小二乘回归分析结果

2 综合评价

2.1 孔隙结构对孔隙度的影响

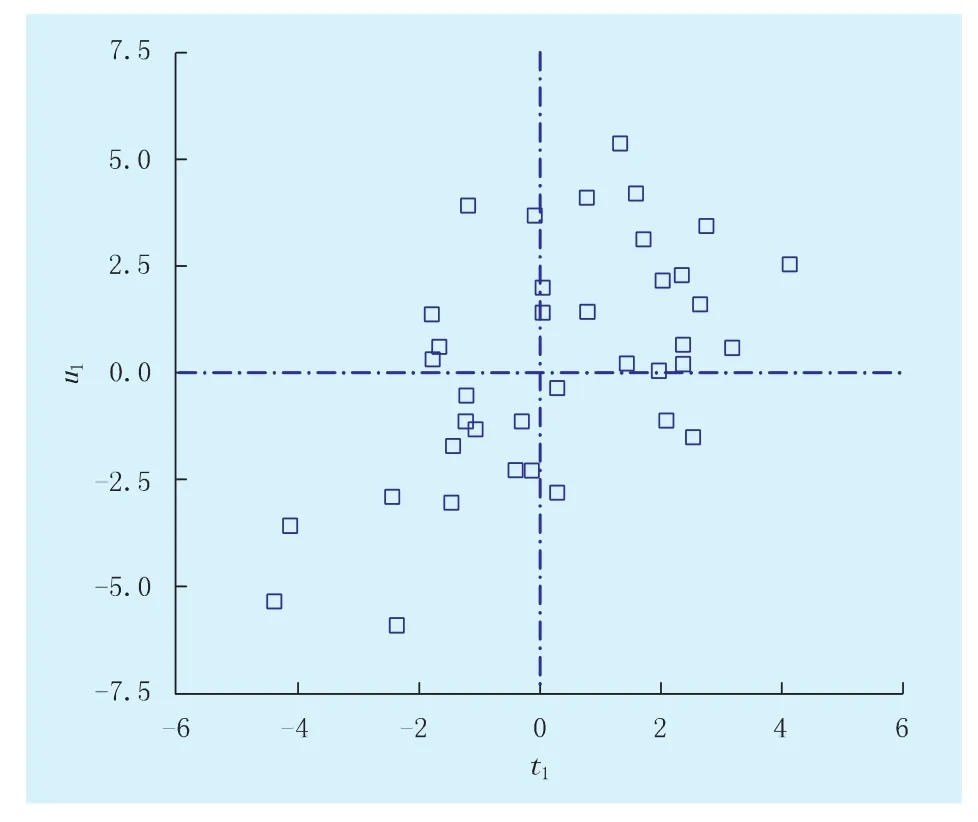
图1 孔隙度偏最小二乘回归模型的u1/t1散点平面图

为了检验孔隙度偏最小二乘回归模型(表1)的可靠性，本文利用因变量主成分u1和自变量主成分t1构成的u1/t1散点平面图作为初步判断依据(图1)。由图1可知:因变量y和自变量x之间存在较明显的线性关系，因而孔隙度偏最小二乘回归模型设定较合理;同时，本文利用还原后的非标准化孔隙度回归方程(y1=23.2101－6.6592x1+0.8215x2+0.0869x3－1.0177x4－0.1070x5－3.9636x6－0.0158x7－0.4185x8)以及参与回归建模的41组实际数据进行回判计算，并用实测孔隙度数据与之对比检验其预测效果(图2)。由图2可知:计算孔隙度与实测孔隙度的吻合程度比较高，平均绝对误差为1.22%，平均相对误差为7.56%，因而孔隙度偏最小二乘回归模型可以在较大程度上体现主要孔隙结构参数对低渗透砂岩储层孔隙度的影响作用。

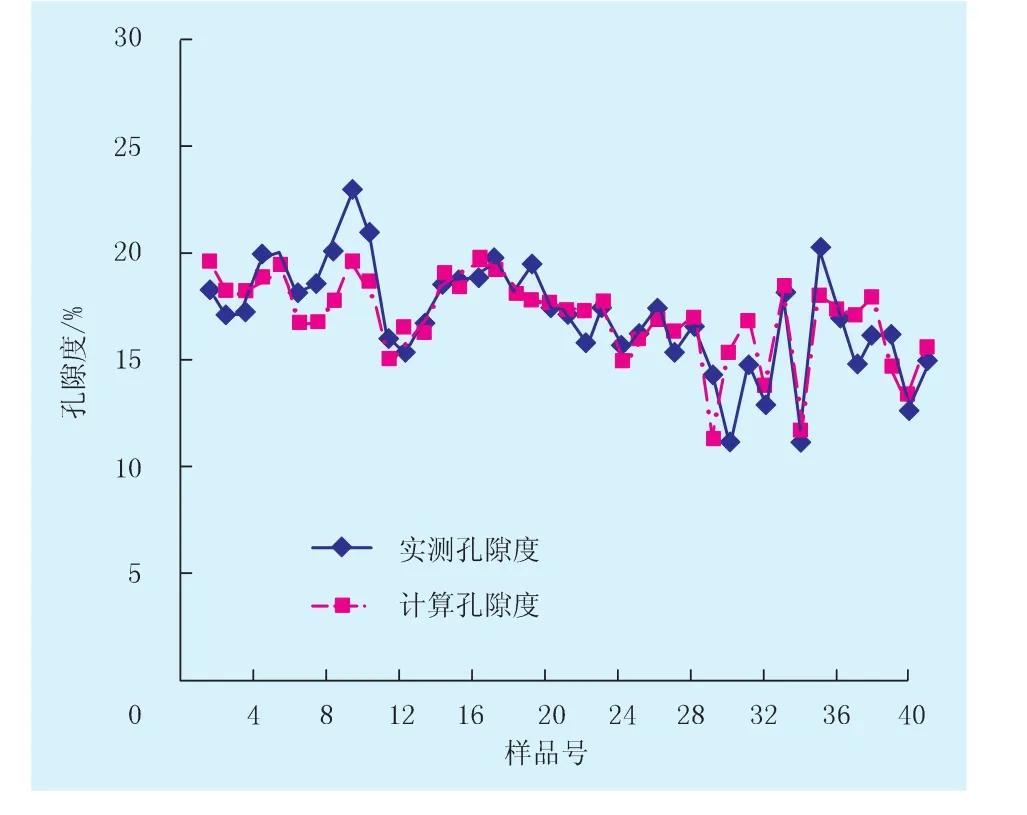
图2 偏最小二乘回归模型的计算孔隙度与实测孔隙度对比

变量投影重要性指标(VIP)可以判断不同自变量对因变量影响的重要性，当某个自变量的VIP＞1时，可认为这个自变量对因变量有显著影响;反之，当某个自变量的VIP＜1时，则可认为这个自变量对因变量只有细微影响。因而，本文通过孔隙度偏最小二乘回归分析获得的不同自变量VIP(表2)可知:排驱压力x1、中值压力x2、孔喉均值x4、变异系数x6的VIP＞1，而其余自变量的VIP＜1;即排驱压力 x1、中值压力 x2、孔喉均值x4、变异系数x6对低渗透砂岩储层孔隙度具有显著的影响作用。

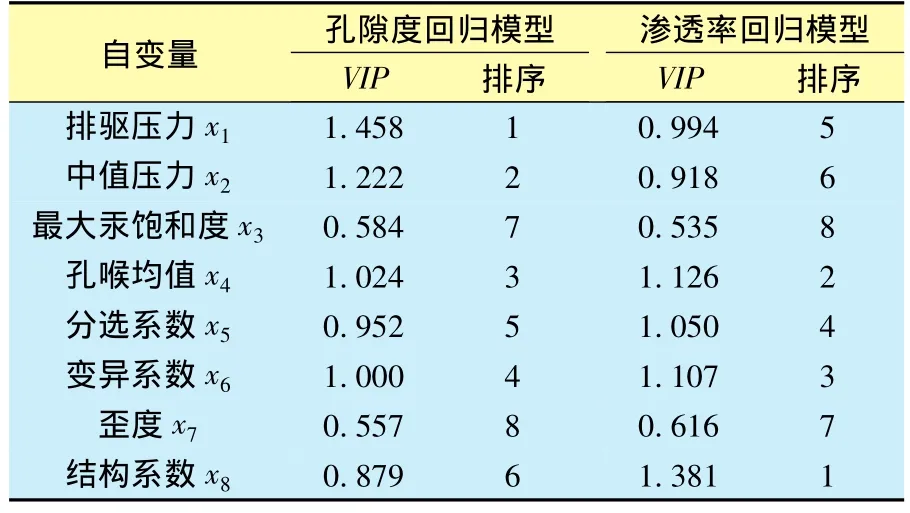
表2 自变量投影重要性(VIP)计算结果

同时，由孔隙度偏最小二乘回归模型的标准方程(表1)可知:排驱压力x1、孔喉均值x4、变异系数x6与孔隙度y1是负相关关系，中值压力x2与孔隙度y1则是正相关关系;而且两组自变量权重系数(w*)和因变量回归系数(r)构成的r1/r2散点平面图也显示:孔隙度y1与排驱压力x1、孔喉均值x4、变异系数x6高度负相关，而与中值压力x2明显正相关(图3)，因而排驱压力x1、孔喉均值x4、变异系数x6是影响低渗透砂岩储层孔隙度的主要负面因素、中值压力x2是影响低渗透砂岩储层孔隙度的主要正面因素。

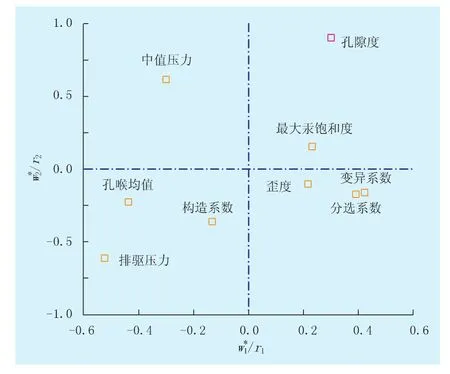
图3 孔隙度偏最小二乘回归模型的r1/r2散点平面图

值得注意的是，尽管上述中值压力作为影响低渗透砂岩储层孔隙度的主要正面因素似乎有悖于人们的一般认识［8－9］(中值压力越大，岩石的渗滤能力越差;反之，岩石的渗滤能力越好)，但这种情况显然与低渗透(尤其超低渗透)砂岩集中以细孔为主的特殊孔隙大小分布特征有着密切关系，如很多低渗透砂岩虽然具有较大的中值压力，但仍然具有较大的孔隙度。此外，本文孔隙度偏最小二乘回归模型对孔隙度y1的累积解释能力只达到了0.642(表1)，这反映了孔隙结构只是影响低渗透砂岩储层孔隙度大小的1个重要因素，诸多其他复杂地质因素都会或多或少、或正面或负面影响低渗透砂岩储层孔隙度的大小［10－11］。

2.2 孔隙结构对渗透率的影响

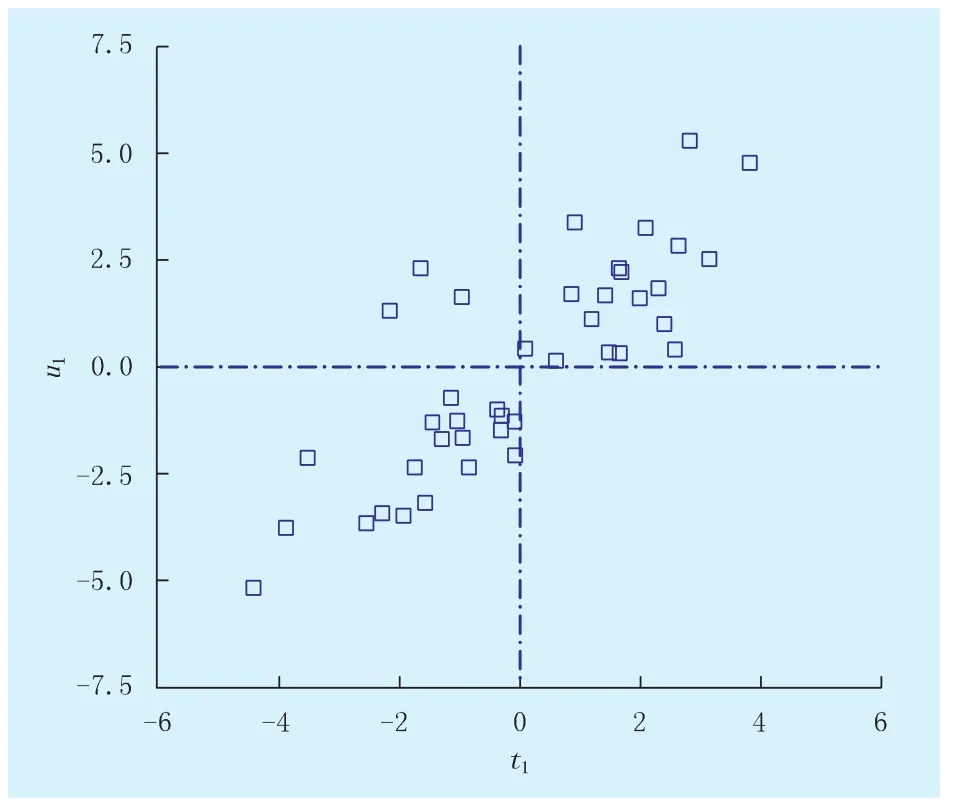
图4 渗透率偏最小二乘回归模型的u1/t1散点平面图

同样，为了检验渗透率偏最小二乘回归模型(表1)的可靠性，本文利用u1/t1散点平面图作为初步判断依据(图4)。由图4可知:因变量y和自变量x之间存在明显的线性关系，因而渗透率偏最小二乘回归模型设定合理;同时，本文利用还原后的非标准化渗透率回归方程(lny2=16.3539－0.8552x1+0.1267x2－0.0120x3－1.1349x4－0.1071x5+2.1824x6+0.5951x7－0.6948x8)以及参与回归建模的41组实际数据进行回判计算，并用实测渗透率数据与之对比检验其预测效果。由图5可知:计算渗透率与实测渗透率的吻合程度比较高，平均绝对误差为2.39×10－3μm2，平均相对误差为32.4%，因而渗透率偏最小二乘回归模型同样可以在较大程度上体现主要孔隙结构参数对低渗透砂岩储层渗透率的影响作用。

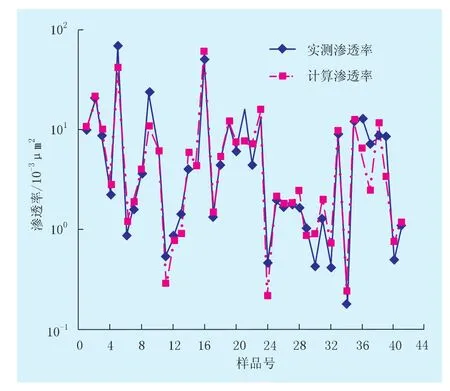
图5 偏最小二乘回归模型的计算渗透率与实测渗透率对比图

本文也通过渗透率偏最小二乘回归分析获得的不同自变量VIP(表2)可知:结构系数x8、孔喉均值x4、变异系数x6、分选系数x5的VIP＞1，而其余自变量的VIP＜1;即结构系数x8、孔喉均值x4、变异系数x6、分选系数x5对低渗透砂岩储层渗透率具有显著的影响作用。同时，由渗透率偏最小二乘回归模型的标准方程(表1)可知:结构系数x8、孔喉均值x4、分选系数x5与渗透率y2是负相关关系，变异系数x6与渗透率y2则是正相关关系;而且r1/r2散点平面图也显示:渗透率y2与结构系数x8、孔喉均值x4、分选系数x5高度负相关，而渗透率y2与变异系数x6明显正相关，因而结构系数x8、孔喉均值x4、分选系数x5是影响低渗透砂岩储层渗透率的主要负面因素、变异系数x6是影响低渗透砂岩储层渗透率的主要正面因素。

事实上，由上述偏最小二乘回归分析获得的影响低渗透砂岩储层渗透率的主要因素与人们一般认识一致［8－9］:渗透率较高的岩石往往具有较大的变异系数以及较小的孔喉半径均值、结构系数、分选系数;渗透率较低的岩石则往往具有较小的变异系数以及较大的孔喉半径均值、结构系数、分选系数。此外，本文渗透率偏最小二乘回归模型对渗透率y2的累计解释能力已经达到了0.903(表1)，这直接反映了孔隙结构是影响低渗透砂岩储层渗透率高低的主要因素，即低渗透砂岩孔隙结构直接决定了储层渗透率，因而在今后的低渗透砂岩油气田的勘探开发过程中仍然需要更多关注岩石的微观孔隙结构特征。

3 结论

(1)通过偏最小二乘回归分析法建立的孔隙结构对低渗透砂岩储层质量影响的回归模型具有较好的可靠性和实用性。

(2)排驱压力、孔喉均值、变异系数是影响低渗透砂岩储层孔隙度的主要负面因素，中值压力则是影响低渗透砂岩储层孔隙度的主要正面因素。

(3)结构系数、孔喉均值、分选系数是影响低渗透砂岩储层渗透率的主要负面因素，变异系数则是影响低渗透砂岩储层渗透率的主要正面因素。

(4)偏最小二乘回归分析法可以为评价孔隙结构对低渗透砂岩储层质量的影响提供一些有价值的基础资料和思考方向。

［1］胡文瑞.中国低渗透油气的现状与未来［J］.中国工程科学，2009，11(8):29－37.

［2］王允诚.油气储层评价［M］.北京:石油工业出版社，1999:75－141.

［3］杨希濮，孙卫.鄂尔多斯盆地低渗透油藏孔隙结构特征及影响因素分析［J］.特种油气藏，2011，18(6):44－47.

［4］胡作维，黄思静，马永坤，等.鄂尔多斯盆地姬塬地区长2油层组砂岩储层孔隙结构特征［J］.断块油气田，2012，19(5):588－591.

［5］Wold S，Albano C，Dunn LLL W J，et al.Pattern recognition:finding and using regularities in multivariate data［C］//Martens H，Russwurm Jr H.Food research and data analysis:proceedings of the IUFoST symposium.London:Applied Science Publishers，1983:147－188.

［6］王惠文.偏最小二乘回归方法及应用［M］.北京:国防科技出版社，1996:200－234.

［7］王惠文，吴载斌，孟洁.偏最小二乘回归的线性与非线性方法［M］.北京:国防工业出版社，2006:97－127.

［8］罗蛰潭，王允诚.油气储集层的孔隙结构［M］.北京:科学出版社，1986:80－139.

［9］王允诚.油层物理学［M］.北京:石油工业出版社，1993:160－197.

［10］沈立成，黄思静，刘洁，等.用多元逐步回归方法评价储层孔隙度的控制因素［J］.成都理工学院学报，2002，29(6):610－616.

［11］蒲秀刚，黄志龙，周建生，等.孔隙结构对碎屑储集岩物性控制作用的定量描述［J］.西安石油大学学报:自然科学版，2006，21(2):15－17，25.