四轴球体研磨机研磨轨迹的研究
2013-10-17程相文王凌霄
程相文,王凌霄
CHENG Xiang-wen,WANG Ling-xiao
(河北联合大学 机械工程学院,唐山 063009)
0 引言
研磨技术已经不再仅仅是一种机加工方法,它已经逐渐发展成为一门艺术。研磨加工是超精密加工的重要加工手段,该技术已经发展成为后续抛光和特种加工获得超光滑表面不可缺少的工序,甚至直接通过研磨加工就已经能够获得超光滑表面。主要包括平面研磨,曲面研磨和球面研磨。因为研磨质量的好坏直接关系到工件的工作精度,所以对决定着研磨质量好坏的研磨轨迹行研究是非常必要的。目前关于轨迹的研究逐渐增多,但是主要集中在对平面轨迹的研究[1],关于球面研磨轨迹研究相对较少。能够提出均匀性评价的研究就更少。浙江工业大学的袁巨龙[2]以及河北理工大学的程相文教授[3]对球面研磨轨迹均匀性做了深入细致的研究。本文对四轴球体研磨机的研磨原理以及研磨轨迹进行研究,并且提出研磨轨迹均匀性的评价方法,为加工获得更优质的球面提供评价标准。
1 四轴球体研磨机的结构及其成球条件
1.1 四轴球体研磨机结构介绍
四轴球体研磨机的机构如图1所示。研磨机由空间相互对称布置的四根轴组成。轴在伺服电机的驱动下可以实现正转和反转。四根轴中Ⅰ轴铅锤布置,其余三根轴与水平面成β=19.4712°,并且在水平面的投影的夹角为ψ=120°。这四根轴在空间组成一个正四面体,任意两轴之间的夹角均为φ=109.4712°,四面体的体心也就是所有轴的交点位置,就是被加工球坯的位置。
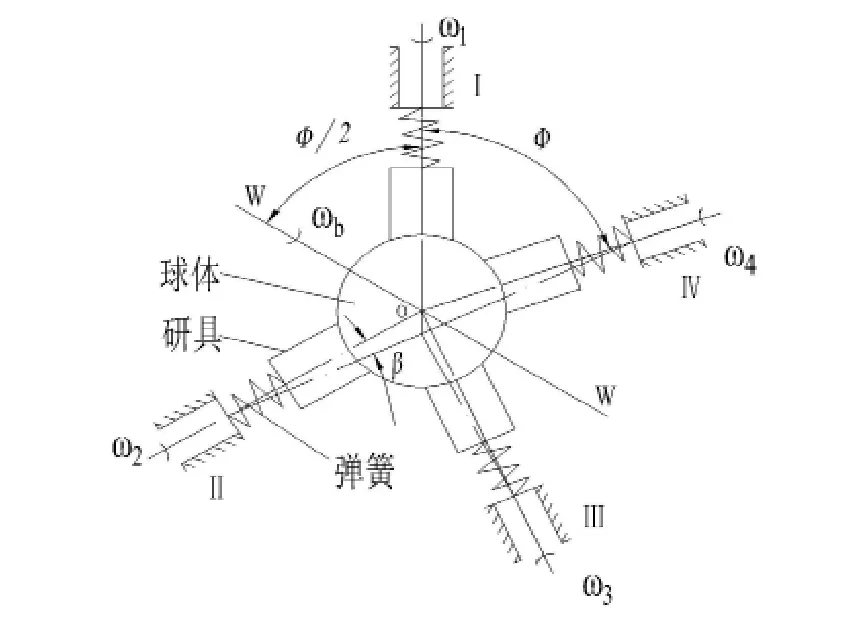
图1 四轴球体研磨机结构简图
1.2 四轴球体研磨机成球条件分析
四根轴的端部分别装有杯状研具,四研具将球坯包络从而进行加工研磨。四根轴拥有相同的转速ωi=ω(i=1,2,3,4)。通过改变轴的正反转向可以改变球体转动轴的位置即改变球坯的自旋角,从而实现球的研磨。真正意义上能够实现球坯研磨的条件是两个研具正转两个研具反转。也就是说只有6种轴的转向组合(见表1)才可以实现球坯研磨。

表1 轴的转向情况
2 研磨轨迹的分析与仿真
2.1 坐标变换
根据坐标转换法,空间直角坐标系上任意一点P0(x0,y0,z0),绕空间任意轴u按逆时针旋转θ角后的坐标为P(x,y,z),他们之间的坐标转换矩阵为:

ux,uy,uz为u在三个轴上的方向向量并且满足ux+uy+uz=1
所以P0和P的转换关系为:

2.2 研磨轨迹分析
四根轴空间位置分布以及各项参数都基本相同,所以四轴上研具相对与工件的轨迹研究方法相同,为了方便轨迹数学模型的建立,在四研具上分别建立局部坐标系ox1y1z1,ox2y2z2,ox3y3z3和ox4y4z4。为了对四研具的轨迹进行统一,需要再建立一个全局坐标系oxyz,由于Ⅰ轴位置的特殊性,所以把Ⅰ轴的局部坐标系作为全局坐标系。如图2所示,原点O为局部坐标系和全局坐标系的坐标原点,oz与Ⅰ重合,x轴位于ⅠOⅡ平面内,且水平。 以研具的轴线为x′轴,z′轴分别在Ⅰ轴和Ⅱ、Ⅲ、Ⅳ轴的平面内,且与x′轴垂直,建立研具局部坐标系的,以研具上一点为研究对象来分析研具的坐标变换。以表1中的第一种情况为例对轨迹进行分析。
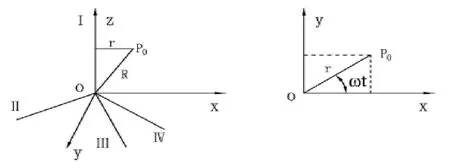
图2 研具的坐标系
研具Ⅰ上任意一点P1(x1、y1、z1)在局部坐标系下的坐标为:

因为研具Ⅰ的局部坐标系和全局坐标系是同一坐标系,所以无需进行坐标转换。
研具Ⅱ上任意一点P2(x2、y2、z2)在局部坐标系下的坐标为:
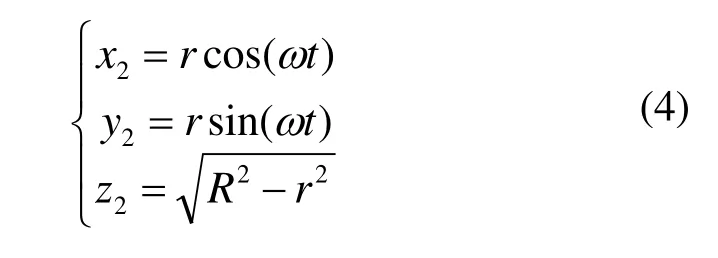
将研具Ⅱ的局部坐标系绕y轴逆时针旋转19.4712°转换到全局坐标系下,转换矩阵为:

研具Ⅲ上任意一点P3(x3、y3、z3)在局部坐标系下的坐标为:

将研具Ⅲ的坐标系绕z轴逆时针旋转120°,再绕y轴逆时针旋转19.4712°变换到全局坐标系,转换矩阵为:

研具Ⅳ任意一点P4(x4、y4、z4)在局部坐标系下的坐标为:
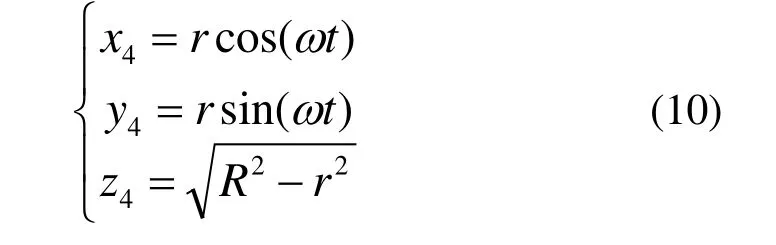
研具Ⅳ的坐标系绕Z轴逆时针旋转240°,再绕Y轴逆时针旋转19.4712°变换到全局坐标系,转换矩阵为:
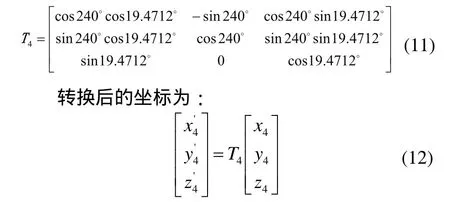
四个轴上的轨迹坐标都已经统一到了全局坐标系下了,接下来按照公式(2)做一次坐标转换就得到了最终的轨迹坐标。因为是以表1的第一种情况作为研究对象,通过几何计算得到转换公式T中ux=cos35.2644°,uy=cos90°,uz=cos54.7356°。这样就能得到最后的轨迹坐标(X,Y,Z)。
研具Ⅰ的运动轨迹方程为:
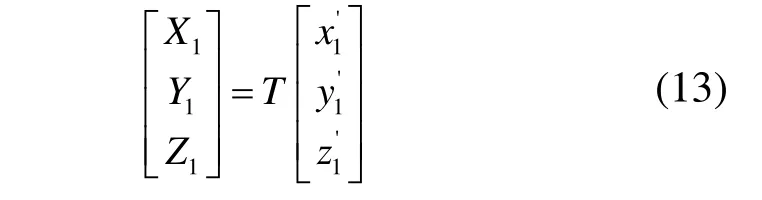
研具Ⅱ的运动轨迹方程为:

研具Ⅲ的运动轨迹方程为:

研具Ⅳ的运动轨迹方程为:

以上是表1中情况1的轨迹推导过程,其他情况的轨迹推导过程与之相同,在此就不再赘述。
2.3 轨迹仿真
以上介绍了情况1研具相对于球体的研磨轨迹方程的推导过程,按照同样的方法分别将其他情况的研具的研磨轨迹方程推导出来。这样能够得到球体研磨六种情况下的轨迹方程。借助Matlab软件,将6种情况研磨轨迹分别进行仿真,结果如图3所示。
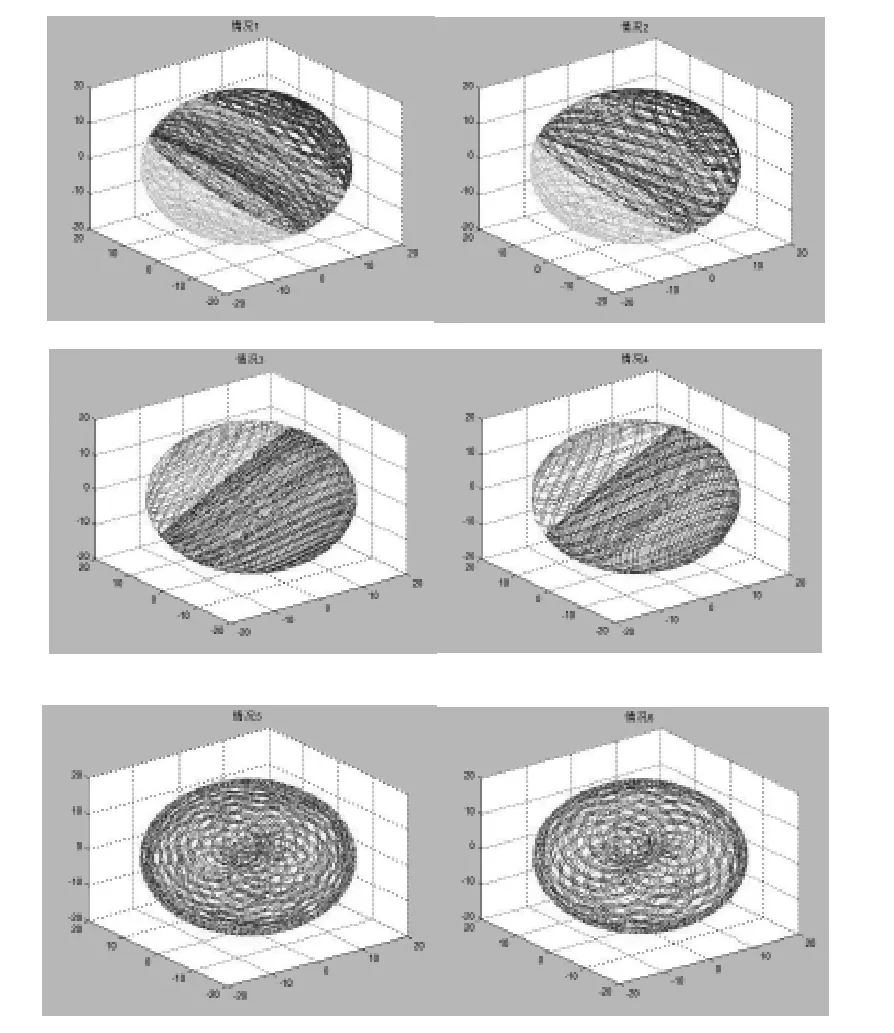
图3 情况1-6研磨轨迹仿真图
由图可见每一种情况的研磨轨迹都能均匀完整的覆盖了整个球体。将六种情况的研磨轨迹叠加,仿真结果如图4所示。仿真结果表明6种研磨情况的叠加能更好的实现研磨轨迹的均匀分布。
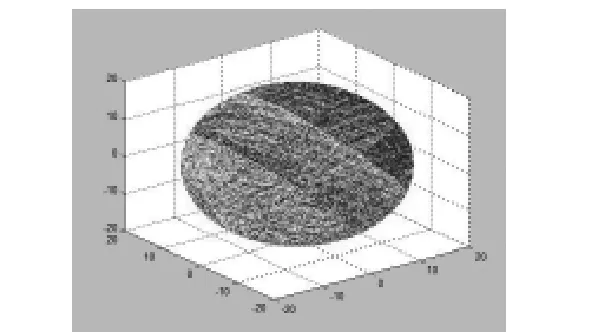
图4 研磨轨迹仿真图
3 研磨轨迹均匀性评价
随着仿真结果的出现,我们发现四轴球研磨机研磨轨迹能均匀的布满整个球面。直观上看研磨效果很好,但是仅仅通过对研磨轨迹仿真图视觉上的观察就对轨迹是否均匀做出评价过于勉强,量化的轨迹均匀性评价对于轨迹评价来说是件必不可少的工作。本文提出通过求解球面上任意一圆环与轨迹交点,把相邻两点间的距离作为轨迹均匀性的评价标准。在球面坐标系下如图5建立一个圆环的方程,为了简化计算过程可以假设一个特殊情况,令φ=0,这样圆环就是在yoz面上的一个圆,将圆环方程和轨迹方程联立,这样方程组就变成时间t和角度θ方程组。

图5 球坐标系
运用matlab软件计算可得到对应t时刻的角度值θ,再计算出任意相邻两个角度的角度差值,这样相邻点间的距离就很容易求得了,再对这些距离求方差,从而就得到了轨迹的均匀性评价标准。图6分别是在100,200,300,400,500秒内轨迹间距的大小。从图的走势来看,随着研磨时间的增加轨迹均匀性呈现越来越好的趋势。
4 结束语
本文通过对四轴球体研磨机机构及其运动特点进行分析研究,并通过坐标转换法对研具相对球坯的运动轨迹进行了研究,模拟仿真了6种情况下的轨迹状况以及最终的轨迹叠加,研磨轨迹能均匀的布满整个球坯,最后又提出一种研磨轨迹均匀性的评价方法,研究结果表明随着研磨的进行,研磨轨迹呈现变好的趋势,对生产加工有指导性建议。
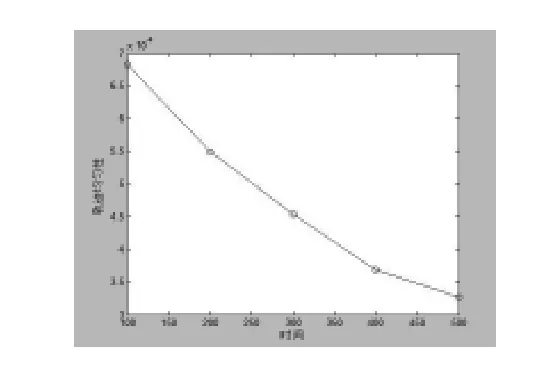
图6 轨迹均匀性
[1] Pei-Lum Tso,et al.A study of carrier motion on a dualface CMP machine[J].Journal of materials processing technology,2001:194-200.
[2] Zhou Z Z,Zheng J J,YuanJ L,et al.Simulation of a ceramic ball lapping process under dual rotating plates lapping mode[J].International Journal of Computer Applications in Technology,2007:2-4.
[3] 程相文,林福严,孙新民,等.静电陀螺仪球形转子的研磨运动轨迹分析[J].工艺与检测,2009:90-93.
[4] 孙新民,李树文,王永梁.四轴球体研磨机的运动学分析[J].机械设计与制造,2000(2):65-67.
