吊拉组合加固中斜拉索索力的参数化分析

鄢生全

(广东长大公路工程有限公司第一分公司)

1 引言

采用斜拉索加固悬索桥完成后，斜拉索在加劲梁处的竖向分力是变化的，即斜拉索协助主缆受力的工作状态是不断变化的，因此确定影响斜拉索索力变化参数的程度对精确分析加固效果至关重要。

2 工程概况

某悬索桥为管线越深沟的构造物，建成于1989年，设计跨度108 m，理论矢高10.8 m，矢跨比为1/10。该桥设两根主缆，主缆由四根钢丝绳组成，钢丝绳规格为 GB1102-74.6×37+1×52-1 600，重力式锚碇。全桥共设35对吊杆，吊杆由Φ26 mm的圆钢加工而成。加劲梁与主塔均采用空间钢桁架结构。

由于提高产量要求，拟对悬索桥进行技术改造提升承载能力，经过方案比选增加8根斜拉索协助主缆受力，以提高主缆的安全系数。

3 斜拉索索状态计算原理

斜拉索计算的常见方法有悬链线法、抛物线法和有限元法，其中悬链线法为精确计算方法，计算公式如下

式中:q为单位索长重量;H为拉索水平方向分力;其余参数意义见图1所示。

图1 悬链线法计算示意图

由积分可得悬链线的长度S为

悬链线由轴力引起的弹性伸长量△S为

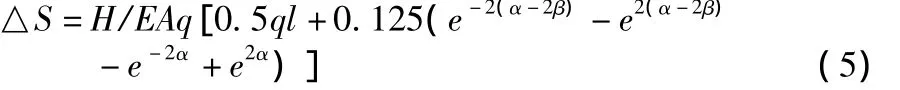
于是，索的无应力索长S0为

温度对无应力索长的影响可以表示为

根据公式(1)～(7)建立方程关系，分析斜拉索张拉后索力随环境温度和位移变化的情况，计算原理如下:(1)斜拉索张拉完成后，根据斜拉索张拉索力以及l、c可以得出张拉完成时环境温度作用下的无应力索长S0;(2)环境温度和l、c发生变化后，由环境温度可得出S温度，根据S温度以及变化后的l、c可得出新斜拉索索力。上述关系建立的方程为超越方程，可以采用迭代法求解。

4 斜拉索索力参数分析

悬索桥加固后，影响斜拉索索力变化的因素主要有参数l和c以及环境温度。该悬索桥斜拉索初始张拉力为85 kN，斜拉索初始张拉温度为10℃，以具有代表性的1号(最短斜拉索)、3号(最长斜拉索)斜拉索为例，分别分析各因素对斜拉索张拉后索力变化的影响情况。1号、3号斜拉索的计算参数见表1。

表1 1号、3号斜拉索计算参数

4.1 环境温度

斜拉索无应力索长随着环境温度发生变化。当环境升温时，斜拉索无应力索长增长，斜拉索索力就会减小;当环境降温时，斜拉索无应力索长减短，斜拉索索力就会增大。

图2 斜拉索索力受环境温度影响情况

由图2可知，1号、3号斜拉索张拉后索力随温度变化的关系近似于线形关系，1号斜拉索的温度-索力关系直线的斜率大于3号斜拉索，环境温度对短斜拉索索力的影响程度大于长斜拉索。

4.2 加劲梁处斜拉索锚固位置位移

加劲梁处斜拉索锚固位置位移包含竖向位移和水平位移。由图3可知，斜拉索3的竖向分力与竖向位移的关系近似于线性关系，而斜拉索1的竖向分力与竖向位移的关系为非线性关系。加劲梁处斜拉索锚固端向下位移时，斜拉索竖向分力显著增大，而向上位移时，斜拉索竖向分力变化较小。短斜拉索的竖向分力受加劲梁处斜拉索锚固端竖向位移影响程度大于长斜拉索。

由图4可知，斜拉索3的竖向分力与水平位移的关系为非线性关系，斜拉索1的竖向分力与水平位移的关系近似于两段斜率不同的直线。加劲梁处斜拉索锚固端向跨中位移时，斜拉索竖向分力显著增大，而向边跨位移时，斜拉索竖向分力变化较小。短斜拉索的竖向分力受加劲梁处斜拉索锚固端水平位移影响程度大于长斜拉索。

图3 斜拉索索力受c的变化值影响情况

图4 斜拉索索力受l的变化值影响情况

4.3 主塔位移

主塔位移包含竖向位移和水平位移。主塔向跨中发生纵向位移时，l值减小，主塔向边跨发生纵向位移时，l值增大;主塔向下发生竖向变形时，c值减小，主塔向上发生竖向变形时，c值增大。

图5 斜拉索索力受主塔纵向位移影响情况

图6 斜拉索索力受主塔竖向位移影响情况

由图5可知，斜拉索加劲梁处竖向分力受主塔纵向位移影响较小，位移-竖向力关系近似于线性关系。

由图6可知，斜拉索加劲梁处竖向分力受向下的主塔竖向变形影响较小，位移-竖向力关系为非线性关系;斜拉索加劲梁处竖向分力受向上的主塔竖向变形影响较大，位移-竖向力关系近似于线性关系。短斜拉索的竖向分力受向下的主塔竖向变形位移影响程度大于长斜拉索。

5 结论

本文以悬链线公式为基础建立了斜拉索索状态力学模型，确定了影响斜拉索张拉后索力变化的因素，研究了各参数的影响程度。根据分析可知，影响张拉后斜拉索索力的主要参数包括环境温度、加劲梁处斜拉索锚固位置竖向位移、加劲梁处斜拉索锚固位置纵向位移、主塔竖向变形，且短斜拉索的竖向分力受各参数影响的程度大于长斜拉索。

根据悬索桥现场量测的数据可知，加劲梁处斜拉索锚固位置纵向位移和主塔竖向位移均小于1 cm，对该悬索桥斜拉索张拉后加劲梁处竖向分力变化影响较小，因此，影响该悬索桥张拉后斜拉索索力的主要参数为环境温度和加劲梁处斜拉索锚固位置竖向位移。正确选取环境温度值，精确计算加劲梁处斜拉索锚固位置竖向位移，才能提高斜拉索张拉后协助主缆受力状态分析的精度。

[1]董晓，张雪松，李宪伟.某悬索桥加固设计与计算[J］.西部交通科技，2009，(29)10:101-105.

[2]卲旭东，张欣，李立峰.斜拉索索状态的精确计算[J］.中南公路工程，2005，30(1):33-35.

[3]包龙生，杨炳成，于玲.吊拉组合索桥的模型建立与初始索力确定[J］.沈阳建筑大学学报，2004，20(4):265-268.

[4]侯俊民，彭晓彬，叶方才.斜拉索索力的温度敏感性[J］.长安大学学报，2002，22(4):34-36.

[5]夏国平，张哲，叶毅.斜拉-悬索协作体系桥的温度效应分析[J］.武汉理工大学学报(交通科学与工程版)，2009，33(5):892-896.

[6]高占凤，杜彦良，苏木标，等.大型结构温度场实时监测系统[J］.铁道学报，2007，29(2):122-125.