非负矩阵分解的快速收敛算法

王桂荣， 林海鹏， 靳庆贵

(1.黑龙江科技大学 机械工程学院，哈尔滨 150022;2.哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001)

0 引言

信号和图形处理中的许多问题可以通过矩阵分解的方式来表达。非负矩阵分解(NMF)最近已被广泛用于稀疏信号和图形分析，甚至是普通数据处理的有效代表。NMF的主要目的是获取数据或信号中潜在的重要结构，进而从这些结构中挖掘出更多生物内在信息。

较系统的 NMF理论1999年由D.D.Lee和H.S.Seung在《Nature》上提出，同时用于人脸识别[1]，引起了科学界的广泛关注。近十几年来，有关NMF方面的算法和应用的理论研究也在积极的进行中。在这些研究中，主要解决不同的代价(损失)函数和附加限制条件可以用来获得不同类型的矩阵分解。在额外的条件限制如非负、稀疏、光滑、低复杂性或较好可预见性等被强加到相互并不独立的信号源上时，非负矩阵分解算法可以用来在盲信号分离中进行有效取出或分离稀疏光滑信源。NMF实际上是对于代价函数进行近似非线性优化问题。

自Lee和Seung提出这两个经典乘性算法后，大量NMF算法被提出，其应用过程中都存在一些限制，如一些NMF算法为了在实际应用中增强某些因子特性，在代价函数中增加一些限制条件，从而形成限制NMF算法。在这些分离中主要包括稀疏性[2－3]、正交性[4]、空间位置[5]、时间连续性[6]和去相关性[7]等等限制条件。

在NMF问题的研究文献中很多使用倍乘更新MU算法对目标函数进行优化，显然MU算法已经成为NMF研究中最受欢迎的。但是对其收敛性的证明却很少涉及。Lee和Seung[8]以欧几里德距离EUC和散度或称为相对熵KL为目标函数来证明，通过MU优化算法目标函数迭代减少。文献[9－10]证明目标函数的限制值既不是局部最小解，也不能连续迭代收敛到固有点。MU算法由于结构简单及易于使用，成为NMF研究的基本算法，因此，对MU算法的收敛性研究显得非常重要。

1 加速算法IILSMU-EUC

阻碍LSMU(Seung的MU算法)算法收敛主要有两个:一是这些乘性公式不能使目标函数足够降低。这一点可以从对LSMU算法形成过程的分析中得出。二是在考虑KKT时W和H可能出现零值。这使得算法不能保证收敛到一阶固有点。

文献[4]提出另一种简单方法解决这种问题，即一个稍微修改的算法(MU被重写为变比例的梯度降低方法并且步进长度相应修改)。主要理论如下:

对于任何常数ε≥0，V≥0和任何(W，H)≥ε，用式(1)更新‖V－WH‖:

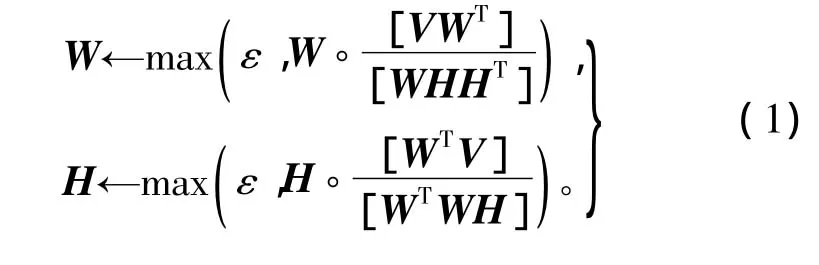
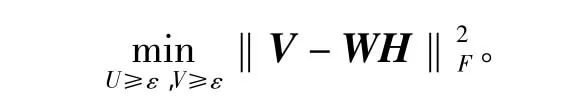
文献[4]提出的改进算法虽然有效，但收敛速度有待提高，在上述改进算法的基础上，重新提出一个加速算法。

1.1 计算量

在MU算法中更新W所需要的计算量要首先确定(对于VT=HTWT，H因子的更新完全与W对称)。原MU是在每次迭代时交替更新W和H。带来的问题是应该更新多少次W，进而更新多少次H都无法确定。即应该执行多少次MU是最好的。

为了确定计算量，先对稀疏和密集矩阵进行有效分析，引入参数K表示在V中非零项的数量。如果V是稀疏的，那么K=mn，假设NMF已经完成压缩(实际中是通常要求的)，这意味着存储W和H比存储V要便宜，粗略地说，在V中非零项的数量一定比W和H的数量大，既K≥r(m+n)。

表1给出在MU更新W矩阵相乘的浮点运算数量(flops)，从中可以查到不同矩阵运算的计算花费，尤其矩阵相乘次序变化时计算花费有很大不同。

函数max使成分智能化，另外，相应算法的每一个限制点是以下优化算法的固有点:

表1 MU更新W运算量Table 1 Flop of W in MU

表1中可以看出:在MU算法中若假设 K≥r(m+n)，第一步计算(A=VHT)计算量是最大的。因此花费时间多的运算步骤应尽可能少的执行，即应该充分利用已经计算出的VHT和HHT矩阵积，在下一次更新H之前，完成更新W多次，即在MU中完成步骤3和4多次。

1.2 内部迭代

从LSMU-EUC算法可以看出，依据浮点运算量，估计出W的第一次更新对下一次是多么费时(H固定时)。由下列迭代因子pW给出(对于H的相应数值由pH给出):

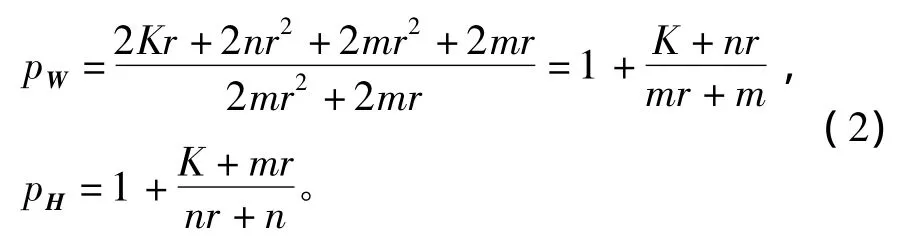
对于不同图像数据库降维的pW和pH的值，如表2所示。由于主要目的是用降维矩阵来提取原矩阵的主要数据特征，为了减少贮存或运算时的数据量，所以降到表示维数。可注意到，对于K≥r(m+n)，看到pW≥2说明W的第一次更新比下一次花费计算多2倍。对于一个密集矩阵K=mn，并且确切，它的确很大，因为n是比r更大的量。例如，当IILSMU-EUC算法对W能更新次的时间花费相当于LSMU-EUC算法两次独立更新。

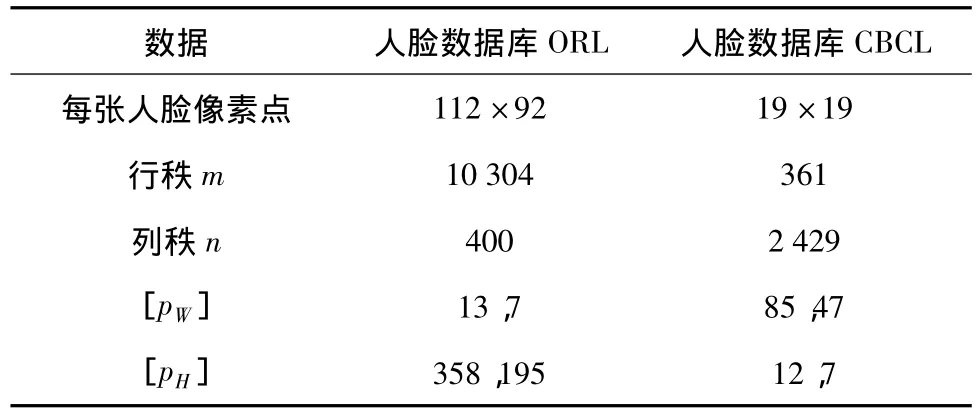
表2 r=30和 r=60时的[pW]、[pH]Table 2 pWand pHwhen r=30 and 60

一个较自然的选择是依赖pW和pH的数值更新W和H一个固定倍数。为了更柔性化可以引入参数a≥0，H的下次更新之前W被更新(1+apW)次;W的下次更新之前H被更新(1+apH)次。

不管怎样，矩阵V的行的数量m和列数量n不在同一个数量级上，例如当n＞＞m时，有，pW＞＞pH。因此，在一方面，矩阵W比H有显著少项(mr＜＜nr)，并且相应NNLS(凸状非负最小二乘)子问题把很少数量变量作为特征;在另一方面，pW＞＞pH和更多W的更新被执行。更明确地说，很多迭代执行在处理简单的问题上，似乎是很不合理的。例如对于CBCL 人脸数据库，有 m=361，n=2 429，r=20，可得到pW≈123、pH=18，用W的上百次更新才能得到NNLS子问题近似优化解显得非常不必要。

1.3 内部迭代停止标准

另一个考虑是什么时候更新W到H(更新H到W)应该使用一个适当的标准，因此采用下列停止标准。W(l)是W的第l次更新的迭代值(保持V固定)。只要满足以下公式停止优化迭代:

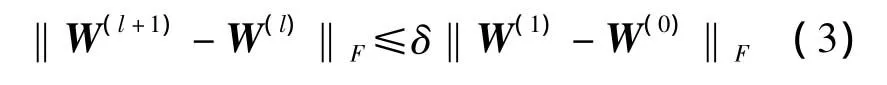
δ是一个小的正数，通过实验发现δ=0.01时取得很好的效果。

1.4 IILSMU-EUC算法

在上述基础上形成新的快速MU算法(IILSMUEUC算法)。要求:数据矩阵V∈和初始化迭代(W，H×Rr×n

(1)当停止标准不满足时计算A=VHT，B=HHT，W(0)=W;

(2)循环(1+apW)次;

(3)使用MU计算W(l);

(4)若‖W(l+1)－W(l)‖F≤0.01‖W(1)－W(0)‖F不满足到(6)步;

(5)到(7)步;

(6)结束如果判断;

(7)结束循环;

(8)W←W(l);

(9)从W更新H，V使用与 W更新相对应(2)～(9)步;

(10)结束。

2 仿真实验

数值仿真实验比较以下算法性能:

(1)LSMU-EUC:Li和 Seung的倍乘算法[8];

(2)IILSMU-EUC:文中提出的快速MU算法;

(3)PG:Lin[11]推荐的映射梯度算法;

(4)HALS:Cichocki和 Zdunek[12]提出的 HALS算法。

所有的测试都在MATLAB7.1，intel Core Dual CPU、内存为1 G的 PC上运行程序。实验取ε=10－16，δ=0.01，降维秩数取 r=60。为了验证算法的真实和有效性，分别针对密集性CBCL人脸数据库和稀疏性ORL人脸数据库图像分别进行实验，结果如下。

2.1 密集性CBCL数据库仿真

CBCL人脸数据库是361×2 429密集型数据库。图1显示目标函数‖V－WH‖对于CBCL密集数据在 a为 0、0.5、1、2和 4时，在 10 s内收敛情况。

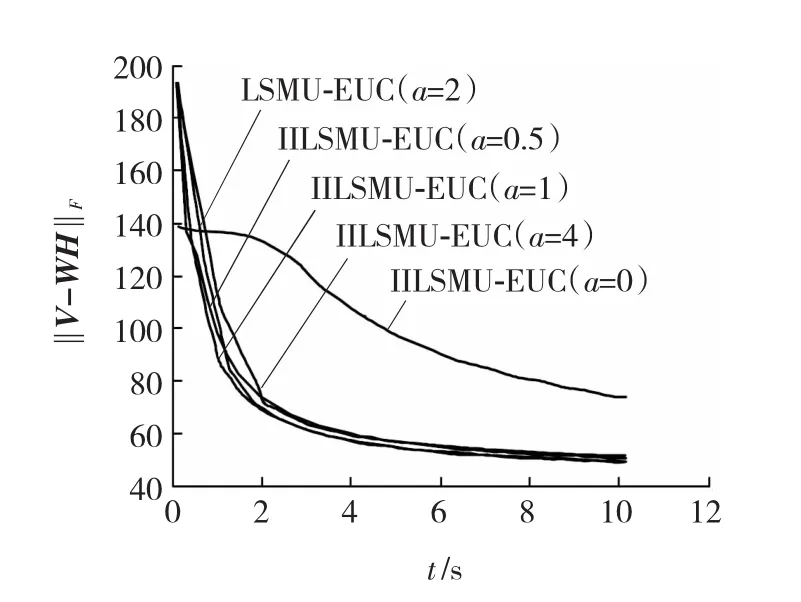
图1 误差曲线Fig.1 Error curve

观察到原LSMU-EUC算法(a=0)除了在初始阶段比 IILSMU-EUC算法误差小外，经过1 s后IILSMU-EUC算法目标函数明显小于原LSMU-EUC算法，说明文中第1部分中分析Lee和Seung的原算法不能够使目标函数足够降低是正确的。IILSMU-EUC算法收敛性显著好于原LSMU-EUC算法，也证明IILSMU-EUC算法的实用价值。另外，对于IILSMU-EUC 算法实验分别取 a=0.5，a=1，a=2，a=4四种情况，可发现只是在最初的2 s内对误差影响较大，但是经过2 s以后IILSMU-EUC算法产生的误差都趋近相同，综合整体性能a=1时加速算法从收敛特性和误差性能都是最好的。

图2是对于CBCL数据库分别采用Lee和Seung的LSMU-EUC算法、IILSMU-EUC算法、Lin提出的PG算法、Cichocki和Zdunek提出的HALS算法进行实验，得出的误差曲线。

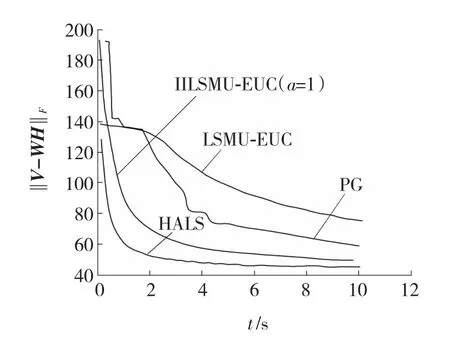
图2 误差曲线Fig.2 Error curve

从图2所示的曲线可以观察到，收敛性顺序如下:LSMU-EUC算法最差，其次PG算法，稍差IILSMU-EUC算法，最好的是HALS;经过10 s后误差也呈现上述排序。但是从算法的复杂性上考虑，PG和HALS算法都远远比MU算法复杂，因此IILSMU-EUC算法比原LSMU-EUC算法性能上有很大提高，又具有算法简单、收敛速度快及易于使用特点。

图3～5分别是CBCL数据库采样、LSMU-EUC算法处理和 IILSMU-EUC算法(a=1)处理后的图像。

图3 CBCL数据库人脸采样Fig.3 Face samples of CBCL

图4 MU算法处理结果Fig.4 MU consequence

图5 IILSMU-EUC算法处理结果Fig.5 IILSMU-EUC consequence

由图5可见，运用IILSMU-EUC算法分解的图像噪声小，主要特征提取明显，其性能上比原算法分解处理的图像(图4)要好。这是由于10 s处理后IILSMU-EUC算法的误差小于原LSMU-EUC算法处理的误差，因此直观的得出文中算法从精密性上好于原算法。

2.2 稀疏性ORL人脸图像仿真

ORL人脸数据库是一个2 576×400稀疏数据矩阵，从图6可以看出，与处理密集数据CBCL时有同样的收敛特性，IILSMU-EUC算法处理的误差曲线在2 s时刻已经变得很小，已经低于LSMU-EUC算法10 s后的误差值，说明IILSMU-EUC算法收敛性明显好于LSMU-EUC算法，IILSMU-EUC算法在a=1时整体性能最佳。

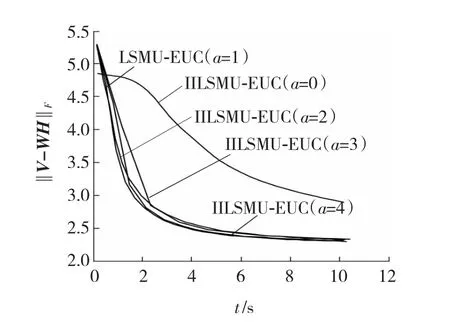
图6 误差曲线Fig.6 Error curve

图7是LSMU-EUC算法、IILSMU-EUC算法、Lin提出的PG算法和HALS算法处理稀疏矩阵ORL时误差曲线比较，从图7中可发现小于4 s时PG误差值大于LSMU-EUC，以后误差值小于LSMU-EUC算法，收敛特性曲线发现HALS最优，其次文中算法，4 s后PG优于LSMU-EUC算法。

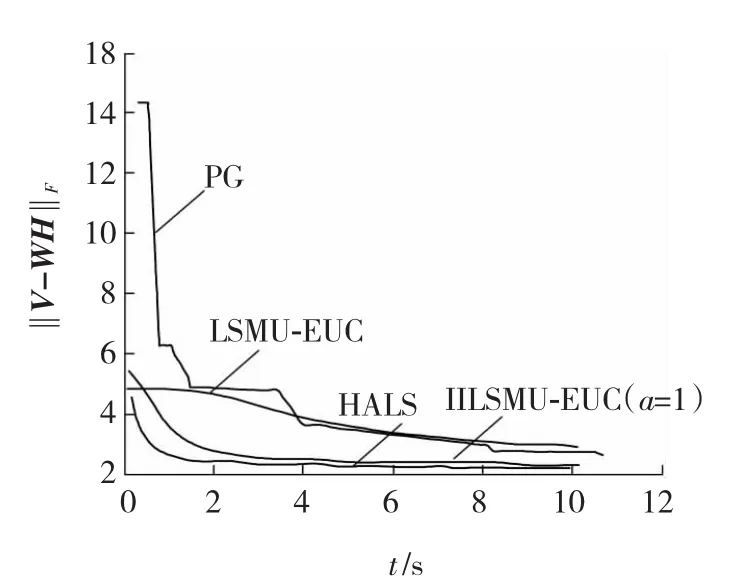
图7 误差曲线Fig.7 Error curve

值得一提的是比较图2与图7，可以看到前者误差大，后者误差小。这是由于对于CBCL降维幅度大，特征提取时误差大。而对于ORL来讲降维幅度小，所以误差小，但这并不影响分析结果。

通过实验证明，无论是对密集数据还是稀疏数据进行NMF处理时，IILSMU-EUC算法(a≠0)的误差曲线上明显好于原LSMU-EUC算法(a=0)，并且在a=1时错误率最少。从图2和图7可得:PG比LSMU-EUC算法优越，一般情况下IILSMU-EUC算法都优于LSMU-EUC算法;IILSMU-EUC算法性能上优于PG算法，略次于HALS算法。

3 结论

在对Lee和Seung的LSMU-EUC算法进行性能分析中找出该算法的缺陷，针对该改进算法的矩阵运算的计算量进行分析，优化计算顺序和考虑迭代方法，提出IILSMU-EUC算法。IILSMU-EUC算法中花费时间多的运算步骤应尽可能少的执行，也就是，充分利用已经计算出的MVT和VVT矩阵积，在下一次更新V之前，完成更新U多次;同样对V更新也同样操作，结果加快迭代收敛速度，提高了分解性能。仿真结果显示在a=1时，IILSMU-EUC算法目标函数明显小于原算法，即新算法收敛速度快;误差曲线分析结果显示，IILSMU-EUC算法优于PG算法，略次于HALS算法，但新算法简单且易于使用;图像分解的对比实验结果说明，新算法对图象主要特征提取明显，噪声小及精密性好。所以IILSMUEUC算法具有算法简单、易于使用和收敛速度快，因此更具有推广价值。

[1]LEE D D，SEUNG H S.Learning the parts of objects by nonnegative matrix factorization[J].Nature，1999，401(4):788 －791.

[2]HOYER P O.Non negative matrix factorization with sparseness constraints[J].Mach Learning，2004，5(9):1457 －1469.

[3]CHOI S.Algorithms for orthogonal nonnegative matrix factorization[C]//In Proc of IEEE International Joint Conference on Neural，USA:Networks，2008:1828 －1832.

[4]LI S，HOU X，ZHANG H，CHENG Q.Learning spatially localized，parts－based representation[C]//In Proc of IEEE Computer Society Conference on Computer Vision and Pattern Recognition，USA:Hawaii，2001:207 －212.

[5]VIRTANEN T.Monaural sound source separation by nonnegative matrix factorization with temporal continuity and sparseness criteria[J].IEEE Transactions on Audio，Speech and Language Processing，2007，15(3):1066－1074.

[6]ZHANG Y，FANG Y.A NMF algorithm for blind separation of uncorrelated signals[C]//In Proc of IEEE International Conference on Wavelet Analysis and Pattern Recognition，China:Beijing，2007:999－1003.

[7]GONZALES E F，ZHANG Y.Accelerating the Lee-Seung algorithm for nonnegative matrix factorization[J].Comput Math Rice Univ Houston，2005，26(3):47－51.

[8]LEE D D，SEUNG H S.Algorithms for non-negative matrix factorization[J].In Advances in Neural Information Processing，2001，13(5):456－460.

[9]LIN C J.On the convergence of multiplicative update algorithms for nonnegative Matrix factorization[J].In IEEE Trans on Neural Networks，2007，8(6):117 －122.

[10]BADEAU R，BERTIN N，VINCENT E.Stability analysis of multiplica-tive update algorithms and application to non-negative matrix factorization[J].IEEE Trans Neural Network，2010，21(12):1869－1881.

[11]LIN C J.Projected gradient methods for nonnegative matrix factorization[J].Neural Computation，2007，19(6):2756 －2779.

[12]CICHOCKI A，ZDUNEK R，AMARI S.Hierarchical ALS algorithms for nonnegative matrix and 3D tensor factorization[J].In Lecture Notes in Computer Science，2007，466(5):169－176.

[13]李 乐，章毓晋.非负矩阵分解算法综述[J].电子学报，2008，36(4):737－743.

[14]张永鹏，郑文超，张晓辉.非负矩阵分解及其在图像压缩中的应用[J].西安邮电学院学报，2008，13(3):58－61.

[15]刘开第，金 斓，庞彦军，等.与判断矩阵一致性无关的单准则排序法[J].河北工程大学学报:自然科学版，2013，30(1):107－112.