基于二阶不确定全局滑模控制的导弹控制器设计＊

董 杰 王法栋 刘宗福

（92785部队 秦皇岛 066200）

1 引言

防空导弹飞行条件复杂，从发射到击中目标整个飞行过程中，飞行高度变化大，飞行速度变化快，且受大气扰流、侧风影响，整个飞行控制系统存在不确定性和非线性特征，很难应用传统经典控制设计方法对其过载跟踪控制系统进行分析设计。滑模变结构控制在导弹控制器设计上有较新的研究和应用，且控制器动态性能优异，跟踪稳定，误差较小。

文献［1］将输出跟踪转化为状态跟踪，采用二阶全局滑模减轻抖振；采用角速度和角加速度信号的滑模控制器有较好的控制性能［2］；文献［3～5］验证了二阶滑模控制系统的动态性能和稳定性能。由于导弹飞行过程中飞行条件变化剧烈，气动、速度等飞行参数存在大范围摄动，使得滑模控制器设计时同样要考虑到不确定性参数的影响。本文应用二阶不确定全局滑模控制，对导弹过载跟踪系统进行分析设计，分析验证了该控制系统的动态性能和鲁棒性能。

2 俯仰通道数学模型

建立包含有不确定参数的大气层内防空导弹弹体模型，参考线性化数学模型［6］，仅以俯仰通道为例进行鲁棒控制器分析设计，得到俯仰通道时变、非线性的数学模型，如式（1）

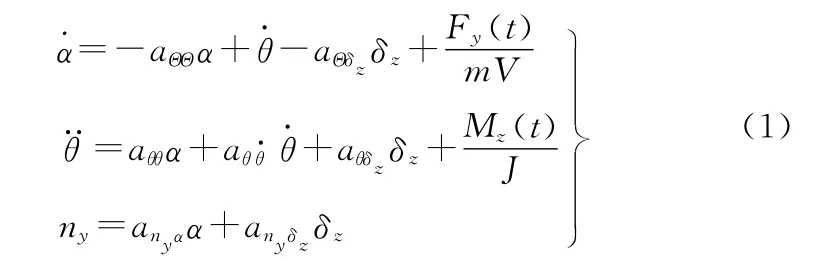
B－1F＜D，D为限定干扰范围的界定函数。

3 滑模控制器设计

设定控制指令为r，则误差为

全局动态滑模面设计为

3.1 控制器设计

控制器设计时，传统滑模变结构控制响应包括趋近模态和滑动模态，该类对参数的不确定性和外部扰动的鲁棒性只存在于滑动模态阶段。全局滑模控制通过动态非线性滑模面实现在响应的全过程具有鲁棒性。由式（1）中已知数学模型的不确定性参数构成，结合各参数±Δ的扰动范围，可以得到式（3）中A，B，F的扰动范围。

则可选取全局滑模控制量u设计为

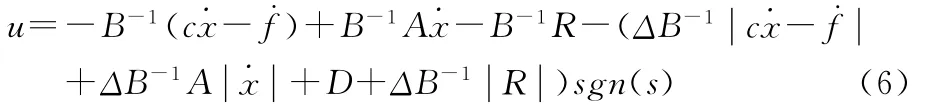
3.2 稳定性分析

定义Lyapunov函数为

由式（5）可得

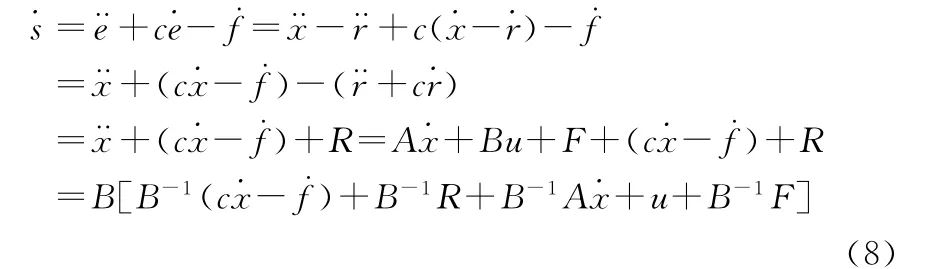
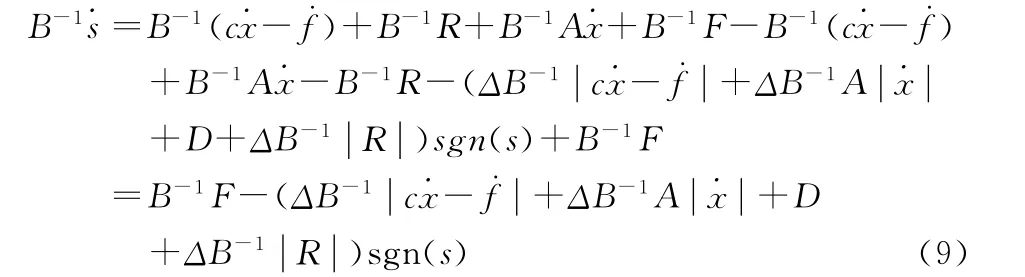
则

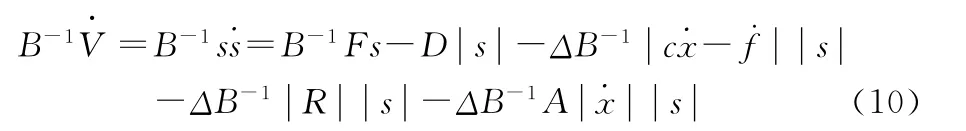
由以上多个等式可得

即证明此时系统稳定。为消除抖振，用饱和函数sat（s）代替控制量中的sgn（s），式（12）中φ为很小的正常数：

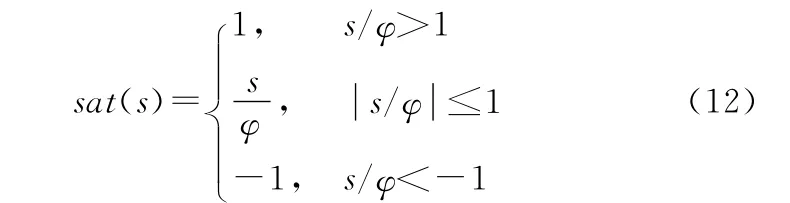
4 算例仿真

取某型防空导弹在飞行高度为4762m，飞行速度为907.2m／s时的相关飞行参数，得到不确定性参数的标称值，依据上节分析，设计包含有不确定性参数的二阶全局滑模控制器。分别应用切换函数和饱和函数进行滑模控制，此时系统响应如图1～3所示。从图中可以看出，过载响应跟踪大小为5g的正弦过载指令时，响应时间短，跟踪精度高，跟踪曲线平滑，误差较小。饱和函数控制性能明显优于切换函数控制性能，能够有效地减少输出存在的频繁抖振。

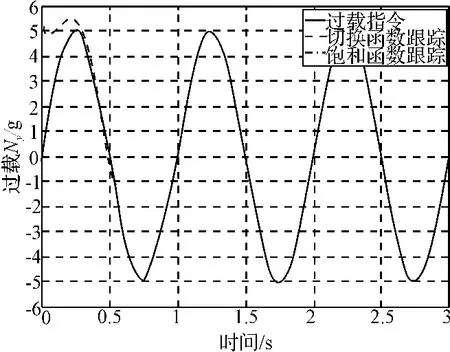
图1 过载响应

图2 角速度响应

图3 s函数响应

考虑扰动范围分别在±10%，±20%，±30%之内时，进行俯仰通道的全局滑模控制器仿真。图4为存在参数摄动时的过载响应，图5为不确定参数条件下的角速度响应，可以看出存在较大范围内的参数摄动时，控制系统输出仍能够保证响应时间快，跟踪精度高，有较高的鲁棒性能。

图4 过载摄动响应

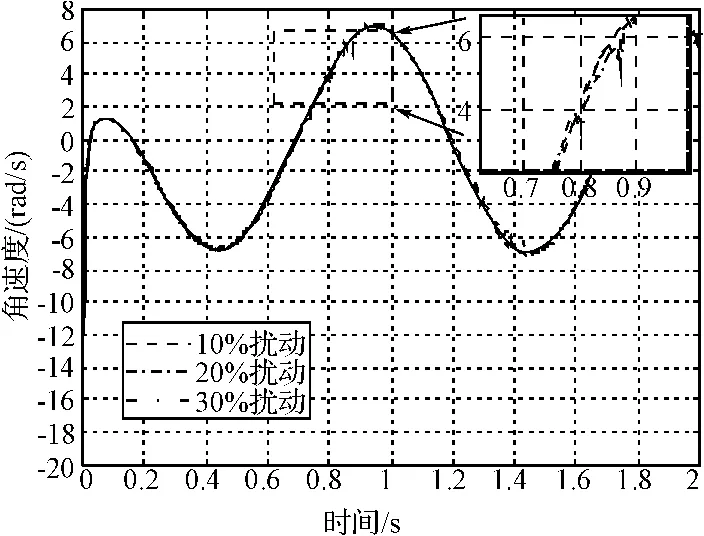
图5 角速度摄动响应

5 结语

通过对包含有不确定性参数的防空导弹控制系统的建模分析，应用二阶不确定全局滑模对过载控制器进行了设计，并通过算例仿真印证了滑模控制器的控制性能；通过使用饱和函数能够有效的减少输出抖振，提高系统的稳定性；在控制器设计时充分考虑到不确定性参数的摄动影响，能够很好地提高滑模控制器的鲁棒性能。二阶不确定全局滑模控制可以保证复杂飞行条件下导弹过载跟踪的稳定性和鲁棒性，提高导弹作战效能。

［1］尚安利，于德海，顾文锦，等.非最小相位导弹自动驾驶仪设计［J］.飞行力学，2005，23（2）：93－96.

［2］梁国强.高性能飞航导弹的一种滑模控制器设计［J］.飞行力学，2006，24（3）：45－48.

［3］尚安利，于德海，顾文锦，等.基于滑模控制理论的导弹自动驾驶仪的设计［J］.南京航空航天大学学报，2005，37（1）：16－19.

［4］尚安利，于德海，顾文锦.基于动态二阶滑模控制算法的导弹自动驾驶仪设计［J］.兵工学报，2006，27（1）：50－53.

［5］顾文锦，尚安利，李聪颖.基于二阶滑模控制的导弹自动驾驶仪设计［J］.飞行力学，2004，22（4）：29－32.