一维距离像扩展目标模拟方法研究*
2013-10-16孔令峰张坤峰
孔令峰 张坤峰
(中国船舶重工集团公司第七二三研究所 扬州 225001)
1 引言
早期雷达系统的目的仅仅是用来确定目标是否存在,并测定它们在空间的位置,其距离分辨率取决于脉冲宽度[1],称为低分辨率雷达。通常认为实际的目标回波与发射信号具有相同的形式。
随着雷达技术的发展及在军事、科技等领域中发挥的巨大作用,人们对雷达功能提出越来越高的要求,希望能够从目标回波中获得尽可能多的目标信息,现代雷达不仅能够高精度地测量目标距离、速度、角度等位置信息,还可以对目标进行成像与识别,其距离分辨率从百米量级提高至米级甚至是分米级。在高分辨率雷达信号的照射下,目标回波与发射信号不再具有相同的形式,目标后向电磁散射在时域上呈现出很多尖锋和低谷[2],常规的“点目标”回波模拟方法已不能满足现代越来越多高分辨率雷达目标回波的模拟要求。本文针对现代高距离分辨率雷达,通过理论分析和仿真计算,探讨了一维距离像扩展目标的模拟方法。
2 一维距离像扩展目标回波信号的形成原理
根据多散射中心理论:光学区复杂目标的后向散射回波可以等效为目标物体上所有散射中心回波的合成[3],可以将距离扩展目标的回波近似为距离像上多个强散射中心对应的点目标回波信号的矢量合成。目标多散射中心及其回波信号能量在径向距离轴上的投影分布称为目标的一维距离像[4],反映了目标的长度、几何结构等重要特征。
一维距离像扩展目标回波形成过程如图1所示。
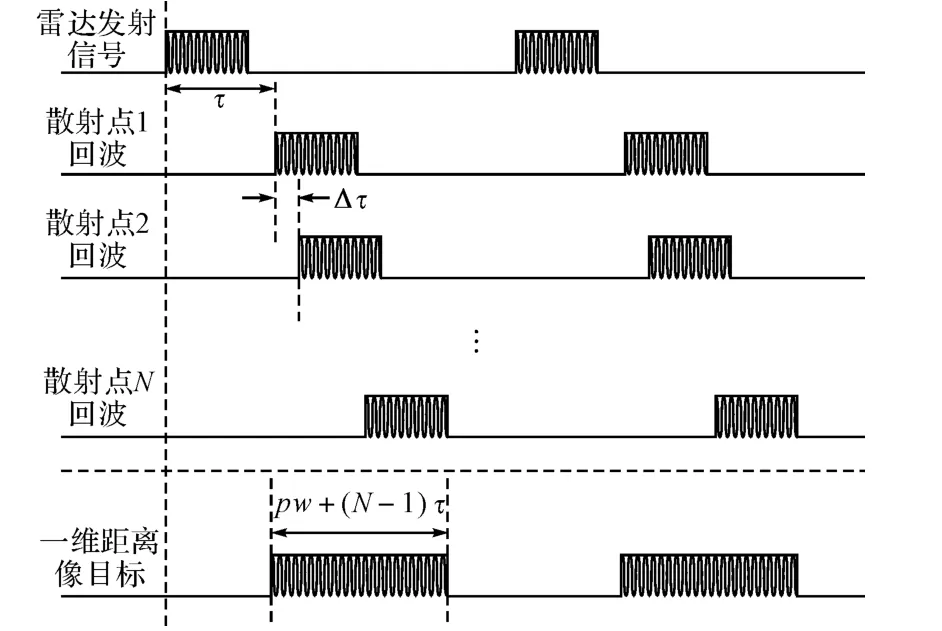
图1 一维距离像扩展目标回波形成原理示意图
3 一维距离像扩展目标回波信号数学模型
基于一维距离像扩展目标回波信号的形成原理,每个分辨单元可以看作是一个独立的点目标,其回波的持续时间为脉宽pw,相邻分辨单元的回波时延为Δτ=2Δr/c,Δr为雷达距离分辨单元,c为电磁波在自由空间中的传播速度。
雷达发射信号的复数形式为
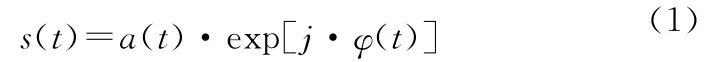
设τi、ri、σi和fdi依次为第i个目标分辨单元的回波时延、径向距离、RCS和多普勒频率,G为发射天线增益,λ为波长,则第i个目标分辨单元的回波信号为
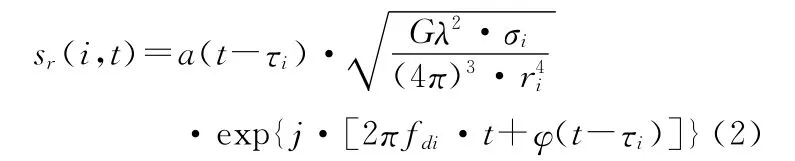
总回波信号为
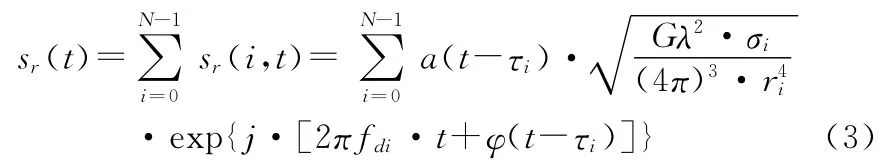
考虑以下因素:1)雷达发射信号功率在脉冲内保持不变;2)目标尺寸相对于雷达到目标的距离很小,各目标分辨单元由于距离造成的衰减差别可忽略不计,可统一按距离r0计算;3)目标尺寸相对于雷达到目标的距离很小,且为径向排布,各目标分辨单元的多普勒频率近似相同。
回波信号可以写为
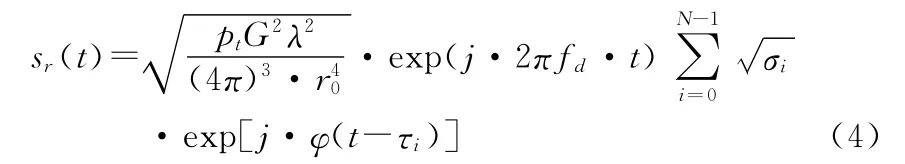
可采用对数正态(Log-Normal)模型、Chi-平方分布(Chi-Square)模型和莱斯分布(rice)模型描述目标分辨单元的 RCS特性[5]。
4 目标RCS调制因子的解算
从扩展目标回波形成的物理过程出发,可通过延迟相加的方法来产生扩展目标回波信号,延迟相加法的实现过程如图2所示。
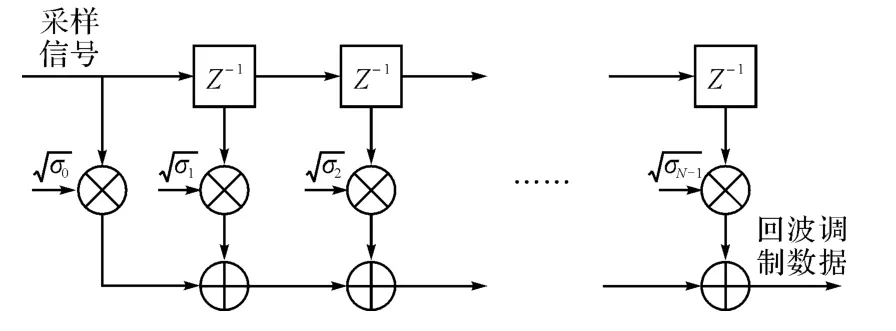
图2 延迟相加法原理图
x(n)与h(n)的线性卷积结果y(n)的点数为L=N+M-1点。若将x(n)前面补充L-N=M-1个0点,将h(n)后面补充L-M=N-1个0点,则线性卷积和圆周卷积有相同的计算结果。根据圆周卷积存在时域卷积对应频域乘积的性质,即 DFT[x(n)*h(n)]=DFT[x(n)]DFT[h(n)]=X(n)H(n),因此,可通过频域变换法计算线性卷积,称为快速卷积[7]。
频域变换法的计算框图如图3所示。
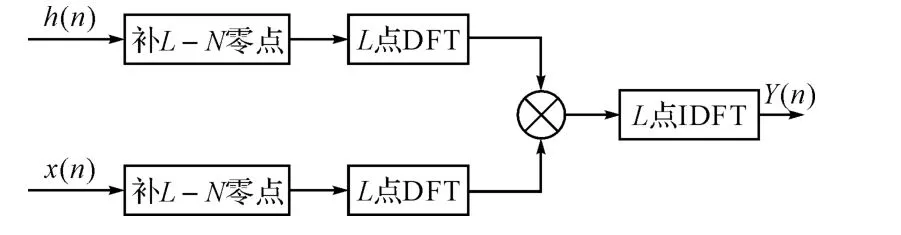
图3 频域变换法原理框图
若L为2的幂次方,则可通过FFT和IFFT进行计算,进一步加快计算速度。
采用频域变换法实现线性卷积运算需要分别对x(n)和h(n)进行补零处理,配成长度为L=N+M-1的两等长序列。在实际应用中经常遇到两个序列的长度相差很大的情况,用上述快速卷积计算线性卷积,要求对短序列补很多0,长序列必须全部输入后才能进行快速计算,因此要求存储容量大,运算时间长,并行处理延时很大,很难实时处理。可采用长序列分段方法进行计算,典型的分段计算方法有重叠相加法和重叠保留法。重叠保留法是在重叠相加法基础上提出来的,其基本思想是:在每段的前端保留原来的输入序列值,用DFT实现圆周卷积,将每段变换结果舍掉重叠部分后的值拼接起来,得到与长序列线性卷积的相同结果[8]。为了不造成输出信号的遗漏,对x(n)分段时,就需使相邻两段有M-1个点的重叠。第一段x(n)由于没有前一段保留信号,则在其前补充M-1个零点值。
5 仿真验证
最常用的四种高距离分辨雷达体制为:线性调频(LFM)连续波雷达、线性调频脉冲压缩雷达、步进频率雷达(SFR)和线性调频兼步进频率的调频步进雷达[9]。本文分别对线性调频脉冲压缩雷达和步进频率雷达的回波信号进行了仿真验证。
1)线性调频脉冲压缩雷达
线性调频脉冲压缩雷达信号的数学表达式为[10]
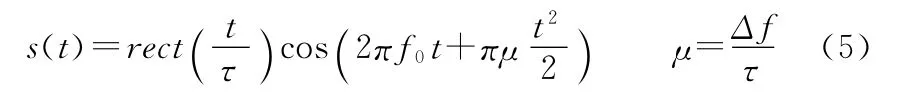
设一距离扩展目标尺寸为0.5μs,相对于雷达的距离为5μs,其分辨单元 RCS依次为1、2、5、3、3,如图4所示。
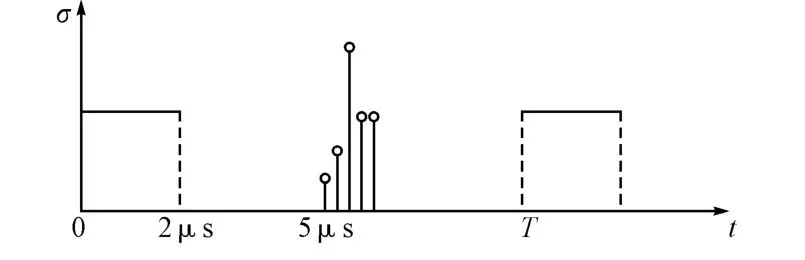
图4 距离扩展目标RCS分布图
仿真结果如图5~图6所示。仿真结果显示,采用本文所述模拟方法产生的扩展目标回波信号,经雷达信号处理后能够形成扩展目标的一维距离像图形。
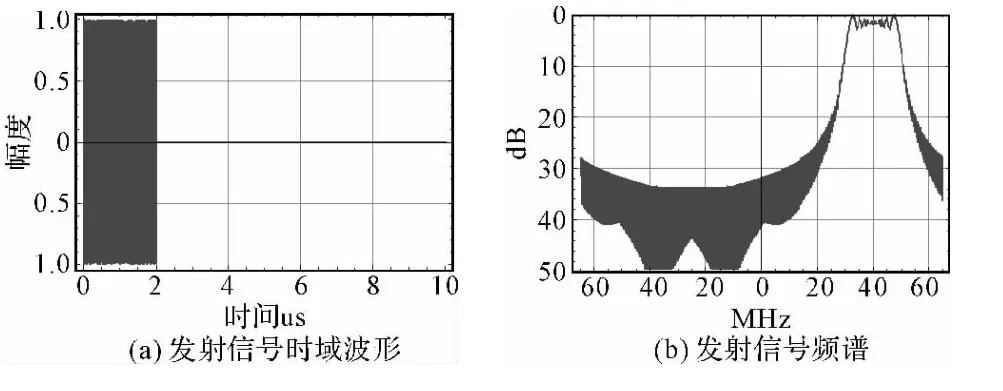
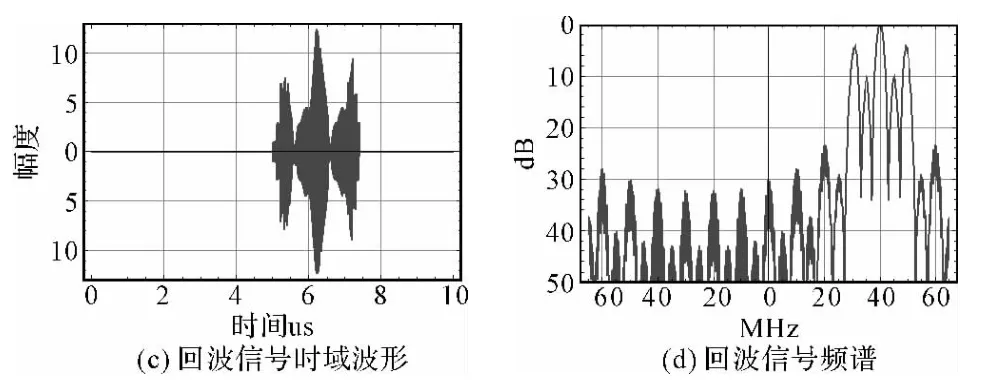
图5 发射信号与回波信号的时域和频域波形
2)频率步进雷达
频率步进雷达信号是由一串载频线性跳变的雷达脉冲组成,通过对脉冲回波的IFFT处理,能够在不增加信号瞬时带宽的情况下通过相参合成获得距离高分辨率[11]。
设置与线性调频同样的目标信息,仿真结果如图7所示。
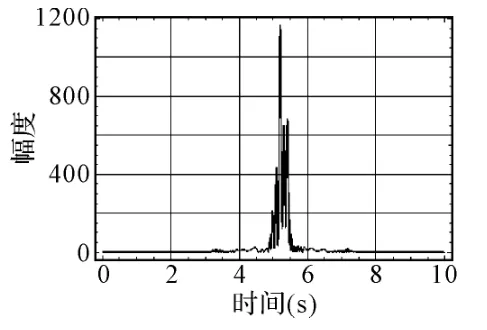
图6 雷达脉冲压缩幅度包络
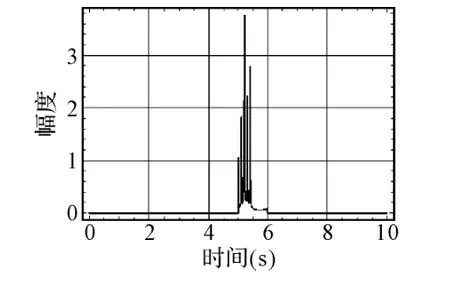
图7 频率步进雷达信号处理结果
6 结语
通过上述仿真分析可知,采用本文所述模拟方法进行一维距离像扩展目标的模拟仿真,能够较为真实地反映高距离分辨率雷达的回波信号特性,满足高距离分辨率雷达的试验需要,对一维距离像扩展目标模拟仿真设备的研制具有较好的指导意义。
[1]丁鹭飞,耿富录.雷达原理[M].修订版.西安:电子科技大学出版社,1997:1-3.
[2]石志广,李为民.雷达目标一维距离像计算仿真研究[J].电光与控制,2006,13(5):31-33.
[3]李娟.距离扩展目标检测与参数估计方法研究[D].长沙:湖南大学,2009:23.
[4]何松华.高距离分辨毫米波雷达目标识别的理论与应用[D].长沙:国防科技大学,1993:10-16.
[5]黄赔康.雷达目标特征信号[M].北京:宇航出版社,1993:51-53.
[6]海因斯.数字信号处理[M].张建华,卓力,张延华,译.北京:科学出版社,2002:9.
[7]赵红怡,张常年.数字信号处理及其MATLAB实现[M].北京:化学工业出版社,2002:21.
[8]徐庆征,彭丽.基于MATLAB的分段卷积计算[J].苏州科技学院学报,2006(2):88-90.
[9]黄德双.高分辨雷达智能信号处理技术[M].第一版.北京:机械工业出版社,2001:33-57.
[10]蔡希尧.雷达系统概论[M].北京:科学出版社,1983:383.
[11]罗鹏,潘健,刘政华.调频步进雷达信号处理的关键问题分析[J].现代雷达,2006,28(8):28-30.
