基于加性加权法的联合作战方案优选＊

杨 槐 冯 涛

（1.陆军军官学院二系 合肥 230031）（2.陆军军官学院研究生队 合肥 230031）

1 引言

联合作战方案是为联合作战指挥员定下决心、提供科学依据的重要步骤，是确保联合作战胜利的基础［1］。传统的作战方案优选，基本上是凭经验和感性认识去分析和处理的。这样的选择，固然可以提高指挥决策的效率，但是这种方法不仅忽略了影响作战方案的诸多潜在因素，还忽略了问题性质的程度上的差异，而这种差异是很重要的。例如在分析作战方案的可接受性时，不能简单地划分为“可接受”、“不可接受”，还必须考虑“可接受性”这个模糊概念的程度如何。联合作战条件下，作战样式众多，情况变化急剧，给优选作战方案带来了许多困难［2］。多属性决策（Multiple Attribute Decision Making，MADM）方法就是一个对属性及方案信息进行处理选择的过程［3］，通过使用此方法，能够从多个指标或准则的角度来综合评估多个联合作战方案，从而为最优方案的确定提供依据。

2 加性加权法［4］

目前对作战方案优选的研究方法主要有：字典序法、理想点法、数据包络分析（简称DEA方法）、神经网络模型、DS证据理论模型、层次分析法等［5］。加性加权法是一种简单易行的多属性决策方法，优点在于实用性、可操作性强。其基本思想是首先对每个方案求各属性值的加权和，然后选择有最大和值的那个方案作为最优方案。

在这种方法中，决策者的偏好用权系数来描述，即决策者根据每个目标的重要程度，分别设定加权系数w1，w2，…，wm，且它们满足wi＞0（i＝1，…，m）。某个目标越重要，其对应的权系数的相对值就越大。设定了各目标的权系数以后，对每个方案求它的各个属性值的加权和，对第i个有：

是第i个方案的第j个属性规范化以后的值。xi反映了第i个候选方案的价值或重要性，则决策者最偏好的方案对应的xi的值应最大且是最优。

该过程可用数学语言描述如下：

已知属性权向量 W ＝［w1，w2，…，wm］T，规范化决策矩阵 A′＝（a′ij）n×m，定义第i个方案的效用ui＝ ∑j∈MWja′ij，则按最大效用准则确定的最优方案x＊满足

本质上，该方法是多属性效用函数方程的特殊形式，因而默认了这样两个假设的正确性，这两个假设是：

1）各属性的效用函数是线性的；

2）属性集满足加性形式所要求的独立性条件。

3 联合作战方案优选模型

联合作战方案优选问题的最大的困难是由于其多维的问题所产生的工作量，所以解决该困难最理想的方法是对每个优选指标都构造一个函数，然后将它们加起来，构成多属性决策问题的价值函数［6］。即有如下形式：

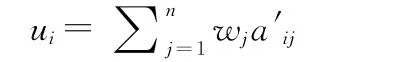
3.1 指标构成［7］

确定联合作战行动方案优选指标，应根据不同的作战样式分别进行。样式不同，指标也就不同，而层次不同，其指标的内涵也不同，如方案级别是战役级或战略级等，还要考虑到将定性指标转化为定量指标以便于分析。优选方案的最终目的是使指挥员能够预见到方案使用后可能发生的结果，据此可将影响优选方案的共性的主要相关因素归纳如下［8］：

1）作战目标实现程度

作战目标是作战行动的目的，联合作战方案的实施是为了实现联合作战的各种作战目标，因此，可以利用完成作战目标的程度来表示。

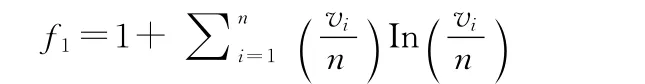
其中，vi表示第i个专家对该程度方面的评分，vi∈［0，1］，n为参与评估专家的数目。

2）作战损耗程度

作战物资损耗，指因战斗使用、损耗等造成的作战物资数量的减少，包括弹药、油料、给养、被装、战救药材、维修器材的损耗量。

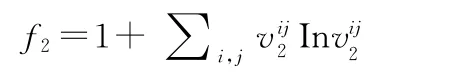
i，j用以区分不同物资以及不同联合参战部队。

3）人员伤亡程度

人员伤亡程度即作战方案实施后所造成的阵亡情况。

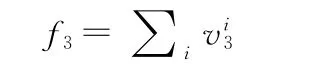
4）敌武器装备损毁程度

武器装备的损毁程度，即预计敌方人员或单位所便用的武器装备在战斗中被毁程度。

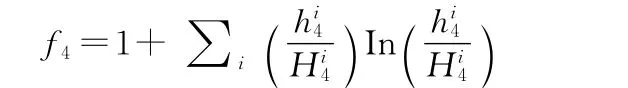
h4i和H4i分别表示敌区分类别武器装备损毁数量和参战武器装备总数。

5）方案风险度

方案风险度，指实施该作战方案产生不利后果的严重程度及其发生损失的概率。

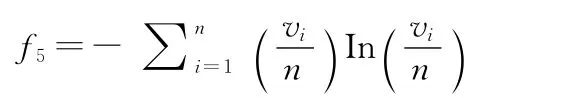
6）方案灵活度

方案灵活度，指作战方案在实施过程中对与主要作战行动方案设想不一致情况的适应能力。

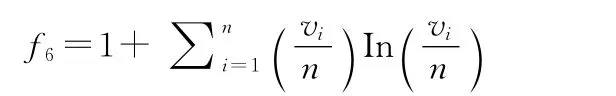
3.2 确定权重

在方案优选过程中，相对于决策者来说，不同指标的重要程度往往是不一样的［9］。因此，在进行多属性决策分析之前，应首先确定每一指标的权值。常用的权值确定方法主要有两类：

第一类是基于决策者自身认识和经验的主观比较法，第二类是基于属性值特征的客观分析法。前者适用于决策矩阵未知的情况；后者适用于决策矩阵已知的情况［10］。本文适用于后者，使用环比评分法确定权重。（见表1）

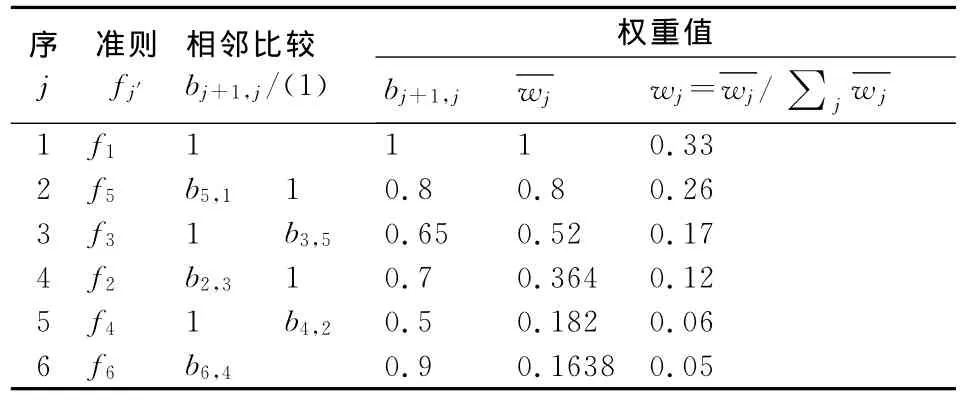
表1 权重值的确定

bj＋1，j表示准则fj＋1与上一个准则fj相对重要性的比值，即

3 实例分析

某部队在联合作战条件下，由作战指挥机关对拟制的4个备选作战方案进行分析论证。已知属性权向量W＝（0.33，0.26，0.17，0.12，0.06，0.06）T，通过公式计算和专家评估，得出量化后的优选指标。（见表2）

表2 量化优选指标

第一步，建立决策矩阵；

第二步，指标规范化；由式

可得

第三步，方案排序。由

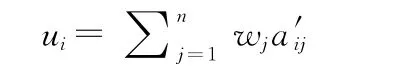
得出u1＝0.823，u2＝0.5834，u3＝0.5175，u4＝0.2586。

可见u1≻u2≻u3≻u4，即方案1优于其他方案。

5 结语

在实际作战中，要使作战方案都能达到每个优选指标的最高要求是不可能的，而且由于指标之间的相互矛盾与制衡，所以不存在通常意义下的最优解，也没有一个放之四海而皆准的优选方法。从理论上讲，每个作战方案优选问题，会有一个与它特点和要求相一致的最合适的优选方法，但实际上要做到这一点非常困难。由于不同优选方法可能会给出不同的结果，故要求决策者不能局限于一种方法，应该将所有方法的结果进行比较后再做出选择。

只要符合联合作战目标要求的程度越高、作战效益越高、风险程度越小、适应战场情况变化程度越高的方案，就是比较好的方案。

［1］袁文先.联合作战指挥机关工作教程［M］.北京：国防大学出版社，2008，3.

［2］党崇民.联合作战参谋工作［M］.北京：解放军出版社，2006，8.

［3］王世云.指挥决策与决策支持［M］.北京：国防大学出版社，2011，10.

［4］魏世孝，周献中.多属性决策理论方法及其在C3I系统中的应用［M］.北京：国防工业出版社，2001，1.

［5］周毅，于正庆.多属性决策在防空兵作战方案选择中的应用［J］.信息工程大学学报，2011（3）：274－277.

［6］倪明，顾婷婷.作战方案信息关联处理方法［J］.指挥信息系统与技术，2012（3）：51－54.

［7］李荣钧.运筹学导论［M］.北京：科学出版社，2009，3.

［8］程启月.基于信息系统的指挥效能评估与风险管理［M］.北京：国防大学出版社，2011，4.

［9］严雷，周庆军，吴奎.基于效果的作战方案优化方法［J］.指挥控制与仿真，2012（2）：48－52.

［10］徐亚军，刘川禾.基于可能度的坦克分队进攻战斗作战方案决策方法［J］.指挥控制与仿真，2011（2）：20－22.