基于信息瓶颈法的图像分离-合并分割算法

李德栋，肖楚琬，庞 威

(1.海军航空工程学院兵器科学与技术系，山东 烟台 264001;2.海军航空工程学院接改装训练大队，山东 烟台 264001)

0 引言

图像分割的主要目的是将一幅图像划分为多个区域，在考虑某个给定标准(如颜色或纹理)时这些区域是匀质的。在图像分析和计算机视觉中，图像分割是一个非常广泛的研究问题，也是通向图像理解的重要步骤。为此已经提出了很多不同的方法，例如阈值法、区域生长法、区域分离-合并法、活动轮廓法以及水平集合法等。每一种方法都只从某一个不同视角考虑分割问题，也只适用于解决少数情况。对于分割算法的研究，可参见文献［1］和文献［2］。

本文的目的是应用信息瓶颈法的基本形式来介绍一种新的分割算法。这种方法的应用需要定义一种信息渠道，这个渠道中一个随机变量通过保留它们之间的最大互信息来控制另一个随机变量的聚类。也就是，此方法的目的是在关于另一变量互信息损失最小的情况下，提取某一随机变量的紧密表征。在分离-合并算法中，这个渠道产生了图像框架和直方图格段之间的相互联系。这种空间信息使得方法在纹理分析方面更加健全，而不用假设任何的优先亮度或是纹理分布。该方法的整体优势在于，它们不要假设任何有关图像的优先信息(如亮度概率分布等)。实验结果表明，信息瓶颈法在处理二维和三维图像分割技术方面是可行的。

1 相关研究

1.1 图像分割

在图像处理中，将图像各部分归类为一种或多种特性同类的多个区域，产生分割后的图像。分割算法一般基于2个亮度值特性之一:不连续性和相似性。第一种特性中，算法基于亮度的突变进行分割图像，比如边缘［3-4］。第二种特性中，主要的方法基于将图像分割成多个区域，依据预先设定的标准这些区域相似。阈值法、区域生长法、直方图聚类法、分离-合并法和随机场法是这一特性方法的典型例子［2，5-10］。

分离-合并算法［1-2，11-12］由2个步骤组成。首先，依据不同标准此方法将整个图像细分为很小的区域。为了分割图像，将采用不同的策略，如四叉树分割(此处每个区域被细分为四等份)和二元空间分割BSP(采用最优的划分来分割区域)。其次，如果符合相似标准，从分割步骤得到的临近区域将被合并。这些相似和不相似标准基于亮度区间、梯度、对比度、区域统计或是纹理。这种分割和合并步骤的组合可考虑任意形状的分割，而不拘泥于垂直或是水平线分割，其只考虑了分割步骤。

1.2 信息论

设Χ为一有限集，X为一随机变量，x在Χ中服从分布p(x)=Pr［X=x］。同样设Y为一随机变量，y属于Y。随机变量X(输入)和Y(输出)之间的信息通道X→Y由一个概率转移矩阵来表征，此矩阵由条件概率构成，其在假定输入的条件下确定输出分布［13］。

随机变量X的香农熵H(X)定义如下:

也可由H(p)表示，估计随机变量X的平均不确定性。所有算法以2为底数，熵用比特数表示。约定0log 0=0。条件熵定义如下:

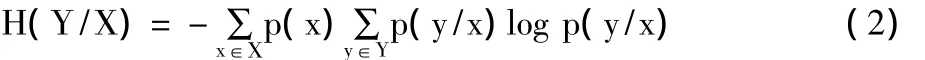
这里，p(y/x)=Pr［Y=y|X=x］为条件概率。如果知道X的输出，条件熵H(Y|X)测量出关于Y的平均不确定性。一般而言，H(Y|X)≠H(X|Y)，且H(X)≥H(X|Y)≥0。

X和Y之间的互信息(MI)定义如下:

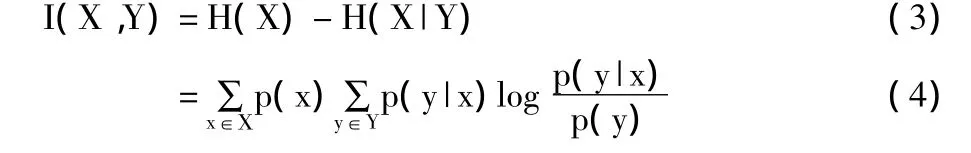
上式计算出了X和Y之间的共享信息。可以看出I(X，Y)=I(Y，X)≥0。MI的一个基本特性由数据处理不等式给出，可用如下方式表示:如果X→Y→Z是马尔科夫链，也就是p(x，y，z)=p(x)p(y|x)p(z|y)，那么:

结果表明:对Y的处理，无论是确定的还是随机的，都不能增加Y包含的关于X的信息量。

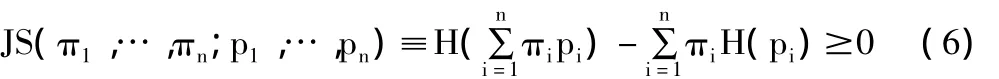
这里，JS(π1，…，πn;p1，…，pn)是具有先验概率的概率分布{p1，…，pn}或满足πi=1的权重{π1，…，πn}的 Jensen-Shannon 散度。JS-散度度量了概率pi来自它们共同发送端的程度πipi，以及当且仅当所有的pi均等时接近0的程度。值得注意，当{π1，…，πn}和{p1，…，pn}分别表示输入分布和通道X→Y的概率转移矩阵时，JS-散度对I(X，Y)来说是恒等的，这里n=|Χ|，m=|Y|。换句话说，πi=p(xi)∀i∈{1，…，n}，pi=p(Y|xi)∀i∈{1，…，n}，p(Y|xi)={p(y1|xi)，…，p(ym|xi)}是条件概率分布。

1.3 信息瓶颈法

由Tishby等［15］提出的信息瓶颈法，提取出了变量X的稠密表征，在关于另一变量Y的互信息MI损失最小情况下由表示(换言之尽可能多地维持有关变量Y的信息)。可采用X的软分割和硬分割。第一种情况下，每簇x∈Χ可通过某个条件概率px)分配给每簇(软聚类)。第二种情况下，每簇x∈Χ只分配给一簇(硬聚类)。

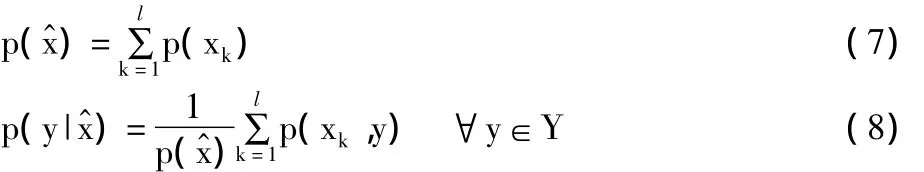
满足以下特性:

(1)由 x1，…，xl融合引起的从 T(X，Y)到 T(，Y)互信息的减少，由下式给出:

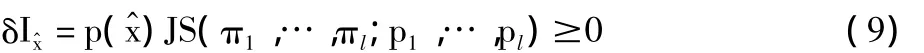
这里，πk=p(xk)/p)，pk=p(Y|xk)。最优的聚类算法进行最小化δI。

(2)l个分量的最优组合可由各组分量的l-1个连续最优组合获得。

Dhillon等［16］提出的联合聚类算法，应用于文字文档聚类，同时使X和Y不相交或硬聚类。最优的联合聚类算法进行最小化I(X，Y)-I(，)的差值。

2 分离-合并算法

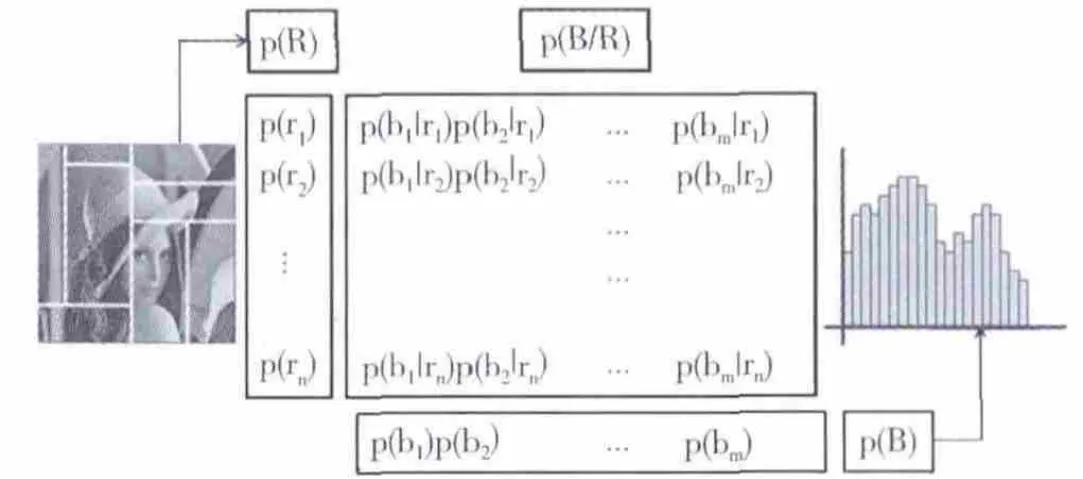
图1 分离-合并算法中图像区域与亮度格段间的信息通道

本节中，提出一种分离-合并算法，它由随机变量R(输入)和B(输出)之间的信息通道R→B构成，2个随机变量分别表示图像的一组区域R和一组亮度格段Β(见图1)。此通道由条件概率矩阵p(B|R)定义，它表示对应于图像每个区域的像素分布于直方图格段的情况。本文中，作为p()自变量的大写字母R和B用来表示概率分布。例如，当p(R)表示区域的输入分布时，p(r)表示单个区域r的概率分布。

假设，图像具有N个像素、Nr个区域和Nb个亮度格段，通道R→B的3个基本元素如下:

(1)条件概率矩阵p(B|R)，表示图像每个区域到直方图格段的转移概率，定义为p(b|r)=n(r，b)/n(r)，这里n(r)是区域r的像素数，n(r，b)是对应于格段b的区域r的像素数。条件概率满足∑b∈Βp(b|r)=1，∀r∈R。

(2)输入分布p(R)，表示选择每个图像区域的概率，定义为p(r)=n(r)/N，也就是区域r的相对面积。

(3)输出分布p(B)，表示每个格段b的归一化频率，由下式给出p(b)=∑r∈Rp(r)p(b|r)=n(b)/N，这里n(b)是对应于格段b的像素数。

2.1 分割

算法的分割阶段是一个期望的自上而下过程，在准均质区域中分割图像。分割策略将整幅图像作为初始分割块，然后根据每个分割步骤的最大互信息增益逐步细分图像。实验中，将应用二元空间分割BSP和四叉树策略。

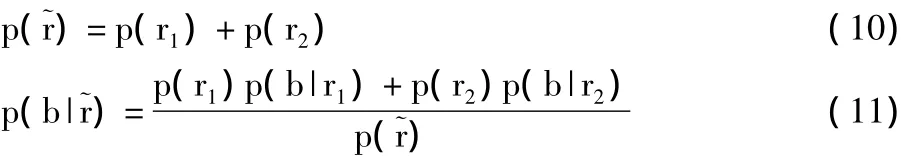
由下式给出:

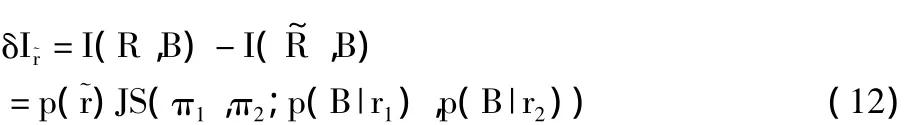
这里，π1=p(r1)/p，π2=p(r2)/p()。2 个区域之间的 JS-散度 JS(π1，π2;p(B|r1)，p(B|r2))，可解释为它们在亮度值方面相异性的度量。也就是，当一个区域被分割时，互信息增益等于分割得到的区域之间相异度乘以区域的尺寸。在分割算法中，最优的分割通过最大化互信息增益δI˜r来得到。

这里，π1=p(r1)/p，π2=p(r2)/p(。2 个区域之间的 JS-散度 JS(π1，π2;p(B|r1)，p(B|r2))，可解释为它们在亮度值方面相异性的度量。也就是，当一个区域被分割时，互信息增益等于分割得到的区域之间相异度乘以区域的尺寸。在分割算法中，最优的分割通过最大化互信息增益δI来得到。

二元空间分割算法可由一个进化的二叉树表示，每一片叶子相当于图像最终的分割区域。每一分割步骤中，二叉树都获得源自原始图像的信息，诸如每一个中间节点k包含源自其对应分割的信息Ik。在某个给定时刻，累加在二叉树中间节点处由p(k)度量的有效信息，可得到I(R，B)，这里p(k)=n(k)/N是与节点k有关的区域的相对面积，n(k)是这个区域的像素数。因此，通道的互信息由下式给出:

这里，T是中间节点的数量。值得强调，最好分割可局部得到。即给定节点k的信息增益Ik独立于图像其它区域的分割水平。

对于式(3)，分割过程也可视为H(B)=I(R，B)+H(B|R)，这里H(B)是直方图熵，I(B，R)和H(B|R)分别表示互信息的连续值和连续分割后得到的条件熵。信息的不断获取增加了I(R，B)，并减少了H(B|R)。条件熵的减少源自分割得到的区域的不断均质化。注意到，可得到的最大互信息是直方图熵H(B)，其在整个过程中保持恒定。分割算法可由互信息增益的比率MIRr=I(R，B)/H(B)或预先设定的区域个数Nr来终止。

2.2 合并

从应用于通道R→B的凝聚信息瓶颈法中，任何用于R的聚类都不会增加I(R，B)值。类似于在分割阶段获得的互信息增益，见式(12)，2个临近区域r1和r2聚类引起的互信息损失由下式给出:

正如在分割阶段所看到的，2个区域之间的JS-散度可解释为它们之间相异性的度量。当2个区域有相同的直方图时相似性达到最大:如果p(B|r1)=p(B|r2)，那么δI^r=0。因此，如果2个区域非常相似(换言之，它们间的JS-散度很小)，可通过由这2个区域的合并取代它们自己来简化通道，而不会有太多信息损失。这就是下面合并算法的指导原则。

从给定的图像分割中，算法连续地合并临近区域对(r1，r2)，这样的δI^r很小。因此，区域数量连同通道的互信息不断地减少。类似于分割算法，停止准则可由比率MIRr=I(R，B)/H(B)或预先设定的区域数量来确定。

这里，H(B|r)是区域r规范化直方图的熵。如果2个区域被聚类

3 算法验证

为了评估本文的方法，将它与文献［17］中提出的手工分割和规范化切割分割作比较。实验采用Berkeley数据库中的100幅测试图像，它们已被手工分割。为了比较不同的分割结果，应用文献［17］中提出的LCE和GCE误差测量法。这些度量定义为:

这里，R(S，pi)表示在分割S中相当于某一区域的像素集合，S包含像素pi，记号表示集合差异，‖x‖是集合x的势。这些度量容许重定义，因此不用太关切分割细节层次的重要性。

因为LCE和GCE的计算都要求分割对，本文评估:(1)一对人工分割;(2)人工分割与分离-合并方法分割对。获得的结果如表1所示，每一行对应于每一个评估情况的平均距离值。在考虑相同图像的不同分割以及不同图像的不同分割时计算每一个度量。在所有的情况下，3个不同分割的结果自动获取，这些分割有相同数量的手工分割区域。另外，附上了文献［17］中当应用规范化切割分割算法得到的结果。注意，这种算法的结果已经在数据库早期获得，只用更少的图像和手工分割。

表1 3种分割算法的总体分割误差

可以看到，相同图像应用分离-合并算法和手工分割获得的分割之间的相似度，比不同图像应用这些方法获得的相似度明显要高。本文的方法应用LCE给出了20%的总体误差(相比于人工分割的5%)，以及应用GCE27%的总体误差(相比于人工分割的8%)。同样可以看到，获得的结果比规范化切割分割算法得到的结果更好。

图2 分离-合并算法的分割结果

分离-合并算法很好地发现了纹理区域的同质性，例如图2(a)中的场地，图2(b)中斑马的皮肤，图2(c)中狒狒头发和图2(d)中的沙滩。这个良好的性能缘于分割(合并)判断是基于区域直方图之间的散度的。尤其是，拥有相同纹理的2个区域具有相似的概率密度函数，因此它们之间的JS-散度很低。在分割阶段，具有相同纹理的一个区域不会被分段，因为互信息增益非常低。另一方面，在合并阶段，这些区域将会被合并，因为互信息损失非常低。因此，每个区域将只显示一种特有的纹理，只有不连接的区域才可能有相同的纹理。

4 结束语

本文介绍了基于信息瓶颈法的图像分割一般框架，并提出了分离-合并算法。该算法定义了图像区域间的信息通道和直方图格段。基于互信息的保存，空间分布和直方图格段最大程度地关联起来。该方法的主要优点是:不用假设关于图像的任何优先信息(例如亮度概率分布)，重视样本的空间分布。在自然图像和医学图像上的不同试验，以及标准算法的比较显示了提出算法的优良性能。

为确定区域和组群的最佳数量，对停止准则的进一步研究是需要的。另一方面，可测试新的分割渠道，重视其它类型的信息，如颜色、纹理和梯度。该方法在图像融合以及细节层次方面的应用将成为下一步研究的重点。

［1］Freixenet J，Muñoz X，Raba D，et al.Yet another survey on image segmentation:Region and boundary information integration［C］//Proc.Eur.Conf.Computer Vision.Copenhagen，Denmark，2002:408-422.

［2］Gonzalez R C，Woods R E.Digital Image Processing［M］.Prentice-Hall，2002.

［3］Canny J.A computational approach to edge detection［J］.IEEE Trans.Pattern Anal.Mach.Intell.，1986，8(6):679-698.

［4］Shi J，Malik J.Normalized cuts and image segmentation［J］.IEEE Trans.Pattern Anal.Mach.Intell.，2000，22(8):888-905.

［5］Chung R H Y，Yung N H C，Cheung P Y S.An efficientparameter less quadrilateral-based image segmentation method［J］.IEEE Trans.Pattern Anal.Mach.Intell.，2005，27(9):1446-1458.

［6］Ballard D H，Brown C M.Computer Vision［M］.Prentice-Hall，1982.

［7］Forsyth D A，Ponce J.Computer Vision:A Modern Approach［M］.Prentice-Hall，2003.

［8］Geman S，Geman D.Stochastic relaxation，gibbs distributions，and the bayesian restoration of images［J］.IEEE Trans.Pattern Anal.Mach.Intell.，1984，6(6):721-741.

［9］Li S.Markov Random Field Modeling in Image Analysis［M］.New York:Springer，2001.

［10］Wu Y T，Shih F Y，Shi J，et al.A top-down region dividing approach for image segmentation［J］.Pattern Recognit.2008，41(6):1948-1960.

［11］Horowitz S L，Pavlidis T.Picture segmentation by a tree traversal algorithm［J］.J.ACM，1976，23(2):368-388.

［12］Suri J，Setarehdan K，Singh S.Advanced Algorithmic Approaches to Medical Image Segmentation［M］.London，:Springer-Verlag，2002.

［13］Cover T M，Thomas J A.Elements of Information Theory［M］.New York:Wiley，1991.

［14］Burbea J，Rao C R.On the convexity of some divergence measures based on entropy functions［J］.IEEE Trans.Inf.Theory，1982，28(3):489-495.

［15］Tishby N，F.Pereira C，Bialek W.The information bottleneck method［C］//Proc.the 37th Annu.Allerton Conf.Communication，Control and Computing.1999:368-377.

［16］Dhillon I S，Mallela S，Modha D S.Information-theoretic co-clustering［C］//Proc.the 9th ACM SIGKDD Int.Conf..2003:89-98.

［17］Martin D，Fowlkes C，Tal D，et al.A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics［C］//Proc.the 8th Int.Conf.Computer Vision.2001:416-423.