Σ-Δ型A/D转换器中量化噪声的功率谱整形

徐国安, 孙德丰, 杜长艳

(1. 吉林大学 教育技术中心, 长春 130012； 2. 中国移动通信集团黑龙江有限公司, 哈尔滨 150028)

0 引 言

当前, Σ-Δ型A/D转换器(ADC: AD Converter)因其优越的性能而得以大量应用在数据采集等众多领域[1]。例如, 在高频雷达信号处理机的多路信号前端输入部分, 往往使用该类型A/D转换器实现数据采集功能。这种A/D转换器所采用的过采样技术能大大降低量化噪声, 其噪声功率谱整形部分设计巧妙[2-4]。但多数文献中对该设计所基于的理论背景往往直接引用, 缺少详尽的理论分析。笔者在建立Σ-Δ型A/D转换器理论模型的基础上, 对过采样技术降低量化噪声这一结论进行分析证明。

1 过采样展宽噪声功率谱

量化噪声是由不可避免的量化误差产生的, 量化误差是一个随机序列, 记为{e(n)}。根据其在具体应用中的实际情况, 对量化误差随机序列可作如下假设[5,6]：

1)e(n)本身是个平稳的随机序列;

2)e(n)本身的任意两个值不相关, 即量化噪声是白的;

3)e(n)的分布为均匀分布, 即符合量化噪声的情况。

通常认为这种噪声与信号之间是加性的[7]。由假设3)可知e(n)的分布为

(1)

这里Δ为均匀量化间隔。进而可求得噪声直流分量和噪声平均功率为

(2)

(3)

为求量化噪声的功率谱密度函数Pe(f), 设噪声功率谱密度函数的数字域形式为Pe(ω), 采样频率为fS。因为已经假设量化噪声是白的, 故Pe(ω)是常数, 并考虑到功率谱密度函数是偶函数, 因此有

(4)

由数字角频率和模拟频率的关系ω=2πf/fS, 将式(4)表示成模拟域形式

(5)

由式(5)可见, 在模拟域内噪声功率仅分布在(0,fS/2)范围内。令

(6)

则式(5)化为

(7)

式(6)即为模拟域量化噪声的功率谱密度函数的定义。Pe(f)在模拟域内应为常数, 故由式(7)得

(8)

有关过采样扩展量化噪声功率谱宽度的原因解释由式(7)和式(8)给出[8]。当采样频率由fS增大到kfS时, 由式(7)可看出, 量化噪声功率在频域的分布范围由原来的(0,fS/2)变为(0,kfS/2)。由式(8)可见, 在(0,kfS/2)频带内噪声功率的强度减小为原来的1/k。其过程如图1所示。这就是过采样技术在频域上扩展量化噪声功率谱宽度的原因。

a 过采样前 b 过采样后

2 噪声功率谱的整形

下面证明高阶Σ-Δ调制器对量化噪声功率谱整形的结论。

a 一阶Σ-Δ调制器框图 b 简化的一阶Σ-Δ调制器频域模型

c 三阶Σ-Δ调制器频域模型

由图2c可得方程

(9)

其中K1,K2,K3分别是3个积分器的放大倍数。如果令

(10)

(11)

则式(9)可化为

Y(f)=HS(f)X(f)+HN(f)Q(f)

(12)

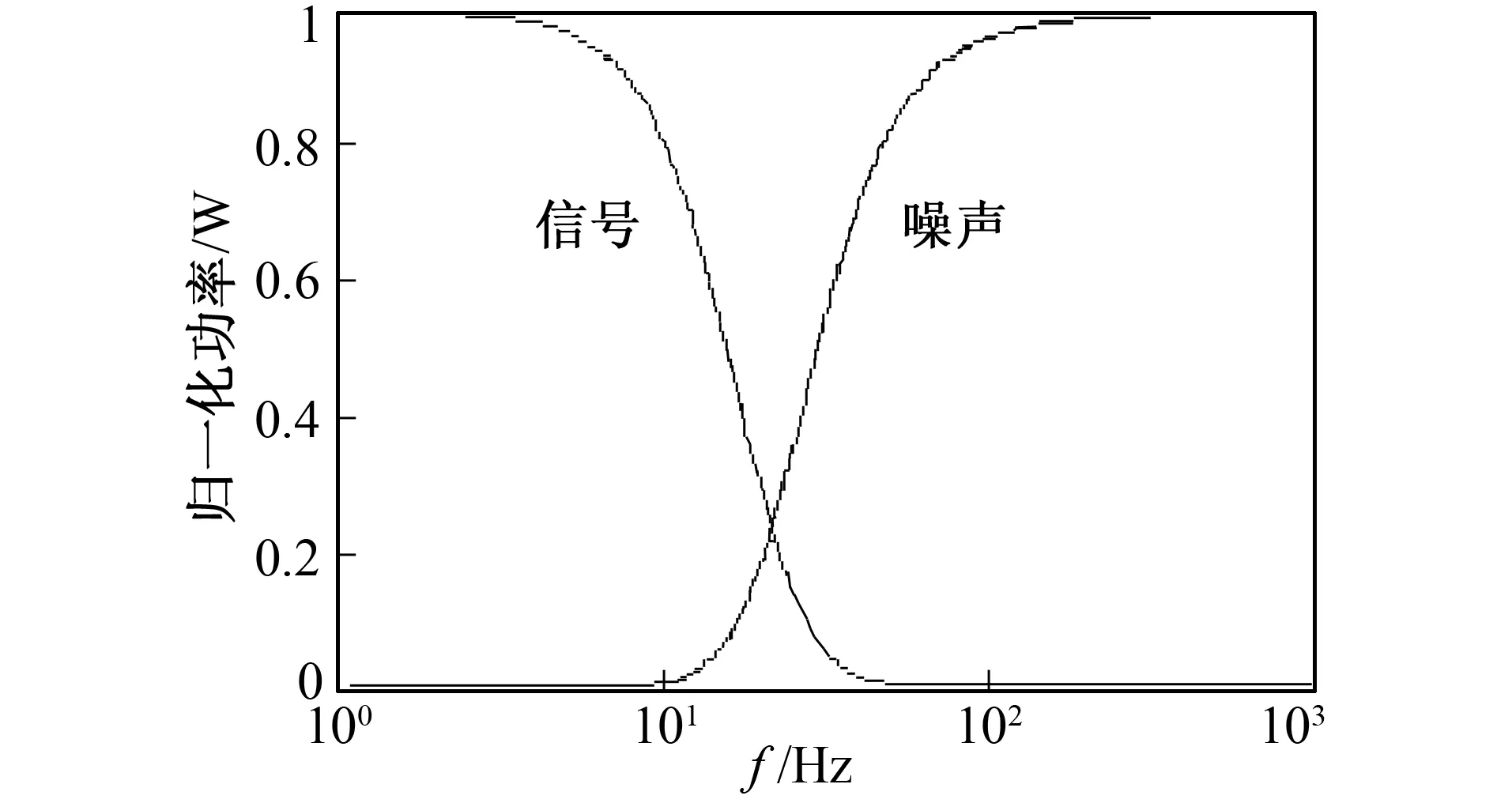
图3 [HS(f)]2和[HN(f)]2的函数关系示意图

其中HS(f)是信号分量,HN(f)是噪声分量。很显然,HS(f)随着f的增大而快速衰减; 对于HN(f), 当f=0时,HN(f)=0, 当f增大时, 它趋于一个常数。由此可见, Σ-Δ调制器对有用信号起“低通”滤波作用, 而对噪声则起“低阻高通”的滤波作用。由能量守恒原理, 无源的Σ-Δ调制器不会改变信号和量化噪声的总功率, 也不会改变其所处的频率范围, 从功率谱的角度看, 其作用实质上是对信号和量化噪声的功率谱进行了整形[10]。

如果将式(12)看成是信号与量化噪声分别通过两个线性系统之后再求和, 则HS(f)和HN(f)就是这两个线性系统的系统函数。对功率谱而言, 一个系统的输出功率谱与输入功率谱之比为系统函数的平方。用Matlab做出的[HS(f)]2和[HN(f)]2的函数图形如图3所示。

由图3可见, Σ-Δ调制器将频带内信号的功率向低频端集中, 而将噪声的功率推向高频端。这就是Σ-Δ调制器对信号和量化噪声功率谱整形的原理。当采用低通滤波器对Σ-Δ调制器的输出端进行低通滤波时, 就会滤除大部分的带外噪声, 而有用信号的功率却得到了加强, 这有利于信噪比的提高[11]。高阶Σ-Δ调制器比低阶的Σ-Δ调制器具有更明显的整形效应。对量化噪声功率谱的整形如图4所示。

a 整形前 b 整形后

3 结 语

Σ-Δ调制器输出的数字信号通常都送入一个高抽取比的数字抽取滤波器, 进行低通滤波, 同时也降低了因过采样带来的高数据输出速率。在低通滤波后的输出数字信号中, 很显然量化噪声受到了抑制, 而有用信号却得到加强。这就是结合Σ-Δ调制技术的过采样技术能降低量化噪声的理论根源。

参考文献：

[1]薛天宇, 孟庆权, 华正权. 模数转换器应用技术 [M]. 北京: 科学出版社, 2001: 19-43.

XUE Tian-yu, MENG Qing-quan, HUA Zheng-quan. Application of AD Convertor [M]. Beijing: Science Press, 2001: 19-43.

[2]克劳切, 拉宾纳. 多抽样率数字信号处理 [M]. 北京: 人民邮电出版社, 1988: 14-62.

CROCHIERE R E, RABINER L E. Digital Signal Processing with Multiple Sample Rates [M]. Beijing: Posts & Telecom Press, 1988: 14-62.

[3]宗孔德. 多抽样率信号处理 [M]. 北京: 清华大学出版社, 1996: 1-9.

ZONG Kong-de. Signal Processing with Multiple Sample Rates [M]. Beijing: Tsinghua University Press, 1996: 1-9.

[4]VRCELJ B, VAIDYANATHAN P P. Equalization with Oversampling in Multiuser CDMA Systems [J]. Signal Processing, IEEE Transactions, 2005, 53(5): 1837-1851.

[5]肖先赐. 现代谱估计—原理与应用 [M]. 哈尔滨: 哈尔滨工业大学出版社, 1991: 1-17.

XIAO Xian-ci. Modern Spectral Estimation-Theory and Its Application [M]. Harbin: Harbin Institute of Technology Press, 1991: 1-17.

[6]CANDY J C, TEMES G C. Over-Sampling Methods for A/D and D/A Conversion [M]. New York: IEEE Press, 1991: 77-84.

[7]王泽华, 王霞. 一种实时语音采样率转换的延迟线算法 [J]. 电声技术, 2008(2): 58-59.

WANG Ze-hua, WANG Xia. An Algorithm of Variance-Time Fractional Delay Line in Changing Sample Rate [J]. Audio Engineering, 2008(2): 58-59.

[8]苗锦, 张剑英, 闫静杰, 等. 采样率转换理论的仿真实现及应用 [J]. 信息技术与信息化, 2008(3): 70-71.

MIAO Jin, ZHANG Jian-ying, YAN Jing-jie, et al. Simulation and Application of Sample Rates Conversion [J]. Information Technology and Informatization, 2008(3): 70-71.

[9]黄志宇, 刘保华. 随机信号的功率谱估计及Matlab的实现 [J]. 现代电子技术, 2001(3): 21-23.

HUANG Zhi-yu, LIU Bao-hua. PSD Estimation for Random Signal and Realization in Matlab [J]. Modern Electronics Technology, 2001(3): 21-23.

[10]GRAY R M. Oversampled Sigma-Delta Modulation [J]. IEEE Trans Commun, 1987, 35(5): 481-489.

[11]朱颖, 何乐年. 高速两阶Sigma-delta调制器研究与设计 [D]. 杭州： 浙江大学超大规模集成电路设计研究所, 2006: 12-20.

ZHU Ying, HE Le-nian. Research and Design of High-Speed Two-Order Sigma-Delta Modulator [D]. Hangzhou: Institute of VLSI Design, Zhejiang University, 2006: 12-20.