基于刚度和模态灵敏度分析的微型客车车架轻量化研究
2013-10-14邢志伟张瑞乾殷亚歆
邢志伟,张瑞乾,殷亚歆
(1.北京信息科技大学 机电工程学院,北京100192;2.长治清华厂技术中心,山西长治 046000)
0 前言
汽车轻量化设计对节能环保有直接的效果。对于传统的内燃机汽车,整车质量每减轻10%,可降低油耗8%左右,降低排放4%[1-2]。而整车质量中的1/3~1/2为车身质量,因此,车身减重对整车减重效果影响很大。
微型客车的车架作为其主要承载结构,承担了由货物、乘客、车身自重带来的弯曲载荷;在不平路面行驶时经轮胎、悬架传递的扭转载荷;同时还包括发动机、底盘系统及路面传来的振动载荷。因此车架需要良好的静动态特性以保证客车整体的刚度、振动特性,扭转刚度、弯曲刚度和模态是车架结构的重要力学性能,反映了车身结构最基本的静动态特性[3]。本文以这三项指标作为约束条件,进行车架的轻量化研究。
由于影响结构性能的设计变量较多,为避免盲目修改,通过灵敏度分析找出对车架结构性能影响较大的参数作为车架优化的设计变量,在保证车身性能的前提下,减少冗余材料,提高材料利用率,从而实现轻量化目标[4]。
1 车架有限元模型建立
分析对象的相关零部件结构CAD数据均通过几何造型软件平台CATIA获得,并转换生成每个零件的stp格式文件。由有限元前后处理软件HyperMesh读入各个零件的stp格式文件。去掉对车架刚度和低阶模态贡献很小的吊钩、安装支架、局部加强件等。由于车架主要是由钣金冲压件经焊接后组成,因此采用壳体单元Quard4和少量Tria3来模拟零件的薄板钣金结构,使用Rbe2单元模拟二氧化碳保护焊、Cweld单元模拟点焊、Rigid模拟螺栓连接,为保证模拟精度同时减小计算量,以10mm为单元基本尺寸建立车架有限元模型如图1所示,完成后包括118385个节点,110895个单元,其中三角形单元1246个,占单元总数的1.1%,焊点总数为1343个。

图1 某微型客车车架有限元模型
车架结构材料定义为各向同性线弹性材料:
杨氏弹性模量E=2.1E+11 Pa;泊松比μ=0.29;质量密度ρ=7.85E+0.3kg/m3。
2 车架模态与刚度计算
2.1 车架模态计算
对车架进行模态分析时,求解目标是车架结构的固有频率和振型,所以忽略外部载荷,进行自由模态分析。基于Lanczos方法对大型板壳单元模态提取时内存占用少,计算速度快,求解精度高的良好表现[5],本文采用Lanczos方法在RADIOSS中提取车架前六阶弹性模态,将计算结果导入HyperView中,得到前六阶模态振型,其中一阶扭转及一阶弯曲振型图(变形放大20倍)如图2,图3所示。

图2 一阶扭转

图3 一阶弯曲
车架前六阶模态见表1。

表1 车架前六阶模态
分析结果表明,车架一阶模态频率为12.2Hz,前车架前端及后车架后端变形较大;一阶弯曲模态频率为19.4Hz,前车架前端变形明显。
2.2 车架扭转刚度计算
计算车架扭转刚度时,采用的边界条件是约束前悬架安装点在车架上的投影点的所有自由度;载荷条件是在两吊耳中间限位支架处,左右分别施加方向相反、大小为3000N的力,左右纵梁下表面各取间隔300mm的15个离散点输出变形;扭转工况下载荷及边界条件如图4。

图4 扭转工况下载荷及边界条件
计算结果显示,左右加载处Z向位移差为8.43mm,车架相对扭转角为0.44°,经计算,扭转刚度为7208.27Nm/deg。扭转工况下左、右纵梁下表面采样点变形图如图5所示,横坐标为采样点的x坐标,纵坐标为该点处节点z向变形值。
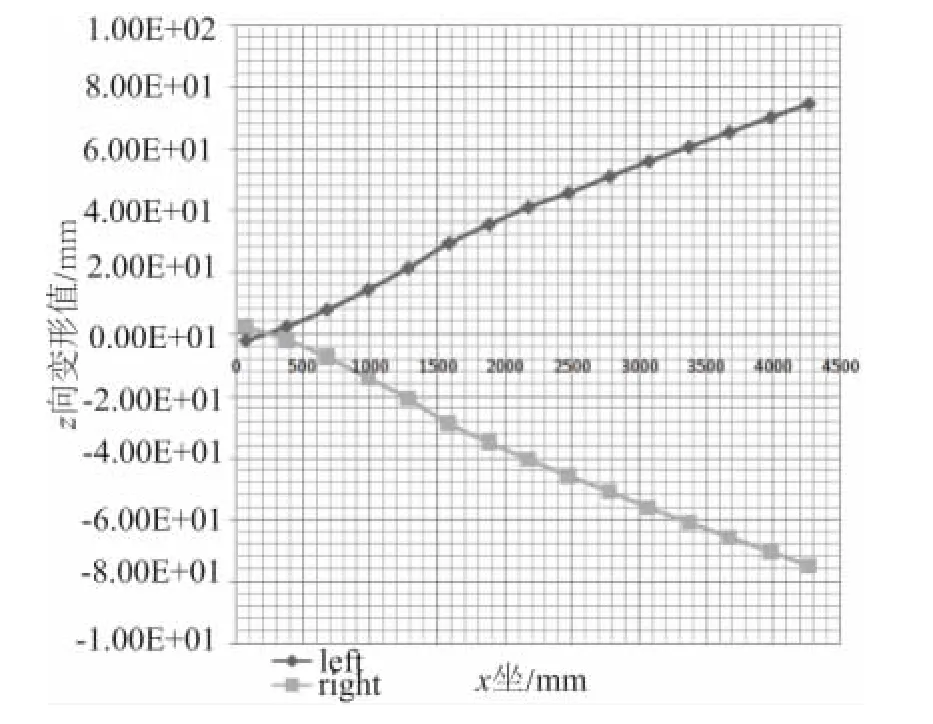
图5 扭转工况变形曲线图
2.3 车架弯曲刚度计算
计算弯曲刚度时,选取的边界条件是约束前悬架安装点在车架上的投影点的所有自由度、约束前后吊耳中间限位支架处除x向平动和绕y轴转动以外的所有自由度;载荷条件是在两侧纵梁中间位置处施加大小为3000N,左右对称、方向垂直向下的力。弯曲工况下载荷及边界条件如图6所示。

图6 弯曲工况下载荷及边界条件

图7 弯曲工况变形曲线图
分析结果显示,左右加载处z向平均位移为2.28mm,计算的车架弯曲刚度为2631.7N/mm。弯曲工况下左、右纵梁采样点变形曲线如图7所示,横坐标为采样点的x坐标,纵坐标为该点处纵梁z向变形值,由于结构对称两侧变形曲线基本重合。
车架在扭转和弯曲工况下的变形图均较为平滑,刚度分布理想。
3 刚度及模态灵敏度分析
通过灵敏度分析可以计算出结构响应值对于各设计变量的导数,以确定设计变化过程中对结构响应最敏感的部分,从而可以获得最关心的灵敏度系数和最佳的设计参数[6]。车架主要结构及装配关系方案已经确定,考虑到改型设计的实际操作性和由此带来的加工制造成本增加,本文选用车架结构零件的厚度作为设计变量。
车架结构的性能参数对车架结构设计变量的灵敏度可以定义为:

式中:uj为第j个函数,这里主要为扭转、弯曲刚度及模态的约束函数和目标函数;xi为函数的第i个设计变量,即第i各零件的料厚。
3.1 灵敏度分析
进行灵敏度分析的约束函数,对于弯曲工况和扭转工况设为车架在加载点处的节点最大位移量,对于模态性能设为第一阶固有频率值;设计变量设为车架部件厚度;目标函数为车架质量最小。
使用HyperWorks/Optistruct模块中的OptiStruct进行计算,定义好灵敏度输出卡片,计算出车架板件厚度对车架扭转刚度、弯曲刚度和一阶模态频率的响应灵敏度,如表2所示。

表2 设计变量模态灵敏度
从计算结果可以看出,后横梁的厚度变化对一阶模态及扭转工况的灵敏度最大,同时,纵梁前段(L)、纵梁后段、纵梁前段(R)、后纵梁盖板后段、拉杆横梁等部件的灵敏度也较高,以上这些部件纵横焊装在一起,构成了车架的抗扭结构。
纵梁后段、前段、左右纵梁上端后加强件、后纵梁后连接板,这些部件对弯曲工况的灵敏度较高,它们都是纵向布置的部件,构成了车架的抗弯结构。
综上所述,灵敏度分析的结果与实际情况相符合,同时快速的确定了影响所关注的动态特性的主要部件,为下一步提出优化措施做好了准备。
3.2 基于灵敏度的优化设计
车架的轻量化设计是以减轻车架总质量为目标,因此定义车架总质量为目标函数(objective),以部件料厚为设计变量,以一阶模态、扭转工况及弯曲工况的加载点位移为约束条件。使用HyperWorks/Optistruct模块进行车架优化计算。定义discrete dvs(离散设计变量值)将设计变量变动范围控制在0.7~2.5mm之间,并且数值分布在0.7,0.8,1.0,1.2,1.3,1.5,1.7,2.0,2.2,2.5mm 以满足生产厂家的配套板材规格。经过14步迭代运算,优化过程结束。部件优化结果如表3所示。

表3 优化部件结果
根据表3调整值,对有限元模型重新赋值进行刚度和模态分析,得到新状态车架扭转刚度为7301.14Nm/deg,有小幅提升;弯曲刚度为2603.6N/mm,基本没有受到削弱;一阶扭转模态频率值为12.0Hz提升了约0.7Hz。改进后车架质量为116.5kg,与修改前的127.2kg相比,减少了10.7kg,占原车架总质量的8.4%。优化前后车架主要性能对比如表4所示。

表4 优化前后主要性能对比
可以看出轻量化效果明显,从轻量化设计的可行角度讲,厚度变化的零件,都可以在现有生产线利用原模具进行加工,改型生产的成本得到了控制。
4 结语
轻量化技术的内涵是采用现代化设计方法对产品进行优化设计,在确保其综合性能指标的情况下,尽可能降低总质量。本文在车架刚度及模态有限元分析的基础上,通过灵敏度分析,对影响车架结构性能的灵敏部件的厚度进行优化设计,加厚灵敏度高的部件,减薄对模态影响较小的部件,实现了轻量化目的。该分析流程同样适用于其他系统乃至整车模型,对产品后续开发有指导意义。
[1]施颐,朱平,等.面向车身前部结构轻量化的试验设计方法研究[J].汽车技术,2010(2):46-50.
[2]Benedyk J.Lisht Metals in Automotive Applications.Lisht Metal-Age,2000,58(10):34-35.
[3]陈鑫.轿车车身静刚度分析及结构优化研究[D].长春:吉林大学硕士学位论文,2002,17-45.
[4]韩旭.基于刚度和模态性能的轿车车身轻量化研究[J].汽车工程,2007(7):545-549.
[5]刘焕广.轿车白车身结构有限元及其试验分析[J].合肥:合肥工业大学硕士论文,2007(4):39.
[6]陈国定,武力.轿车白车身结构的相对灵敏度分析[J].机械设计,2007(4):22-23.
