土壤垂直一维入渗对VG模型参数的敏感性分析

王志涛，缴锡云，韩红亮，虞晓彬

(1.河海大学水文水资源与水利工程科学国家重点实验室，江苏南京 210098;2.河海大学水利水电学院，江苏南京 210098)

随着计算机技术的发展，采用数值计算方法来模拟土壤水分以及溶质运移越来越受到人们的重视，并逐渐成为研究土壤水分运动及溶质运移的主要方法［1］。然而，在进行模拟之前，必须先确定模型中的相关参数，土壤水分特征曲线就是其中必不可少的参数之一［2-4］，其准确程度直接影响到模型的精度。描述土壤水分特征曲线的模型很多［5-6］，应用较多的是Van Genuchten模型［7］(简称VG模型)。

在应用模型进行数值模拟时，测定、分析模型中诸多参数的变化对模拟结果的影响程度，判断各个参数对模拟结果的重要性，这就是参数的敏感性分析。目前，模型参数的敏感性分析大多是针对水文模型而言的［8-9］，对土壤水分运动模型参数敏感性的研究较少。聂卫波等［10-11］对一维垂直入渗过程的数值模拟进行了验证。毕经伟等［12］、孟丽江［13］以底部通量作为敏感性分析指标，得出饱和水力传导度是最敏感的参数、饱和含水率次之。梁冰等［14］分析了VG模型中的α和n这2个经验参数对土壤重力释水和入渗过程的影响，认为α较小时不易于土壤释水过程的进行，但有利于水分入渗;n较小时不利于重力释水的进行，对于入渗过程的影响则较为复杂。

本文以HYDRUS-1D模型［15］模拟土壤垂直一维入渗，采用单因素局部扰动分析方法，分别对VG模型中各个参数进行扰动(扰动幅度为±20%)，研究参数扰动后对湿润锋运移距离、累计入渗量的影响，旨在找到对土壤入渗影响显著的VG模型参数，以便在实际应用时准确地确定敏感性较强的参数，避免在模拟过程中由于参数不精确所带来的误差。

1 入渗模型

1.1 VG模型及试验土壤参数

VG 模型表达式［7］如下:

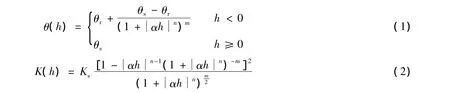
式中:h——压力水头，cm;θr——残余含水率，cm3/cm3;θs——饱和含水率，cm3/cm3;α——土壤特征曲线的经验参数，cm-1;n——土壤特征曲线的经验参数，无量纲;Ks——饱和导水率，cm/min;K(h)——非饱和导水率，cm/min;m——经验系数，m=1-1/n(n ＞1)。

试验用土取自河北省沧州市中国科学院南皮生态农业试验站。利用SEDIMA4-12粒度分析仪(德国)进行颗粒分析，得出该土样为粉壤土(美国制分类标准)，密度为1.40 g/cm3，其砂粒、粉粒、黏粒的质量分数分别为11.84%，66.21%，21.95%。根据土壤的机械组成及土壤密度，应用HYDRUS-1D模型中内置的RETC模块预测 VG 模型参数［15-17］，得出 θr=0.0743cm3/cm3，θs=0.4312cm3/cm3，α =0.0056cm-1，n=1.6345，Ks=0.0107 cm/min。

1.2 边界条件及初始条件

在HYDRUS-1D模型中，土壤质地、密度是通过VG模型中的参数取值体现的。土壤质地、密度对土壤入渗过程的入渗速率、累计入渗量、土壤湿润锋运移距离有较大影响;入渗水头对入渗速率、累计入渗量及土壤湿润锋运移距离影响微弱;初始含水率对入渗速率、累计入渗量的影响也较小，但是对湿润锋运移距离有较明显的影响［10-11］。初始条件和边界条件不会影响VG模型参数的敏感性，故在模拟时土壤初始体积含水率取为恒定值(0.15 cm3/cm3);上边界取为恒定的压力水头(h=2.5 cm);下边界取为自由排水界面。模拟土柱高度为100 cm，模拟时间为750 min。入渗过程中，湿润锋始终未到达下边界，可视为半无限土体，因此下边界压力水头为一恒定压力水头。上、下边界条件分别为

2 入渗过程对VG模型参数的敏感性分析

VG模型参数θr，θs，α，n等扰动显著地影响土壤水分特征曲线的形状。θr和α的扰动均对VG模型曲线的高吸力段(低含水率)影响显著，在中、低吸力段(中、高含水率)扰动曲线逐渐与标准曲线趋于一致;θs的扰动对VG模型曲线高、中、低吸力段均有影响;n的扰动对VG模型曲线的影响最显著，且扰动曲线在饱和含水率处与基准曲线相交。Ks的扰动虽然不影响土壤水分特征曲线的形状，但是Ks决定着土壤导水能力的强弱，对土壤水分运动的影响不容忽视。文献［12-13］指出，Ks和θs是影响底部通量的关键性因素。

2.1 垂直湿润距离计算值

θr，θs和α的扰动与垂直湿润距离计算值Rz呈负相关关系，n和Ks与Rz呈正相关关系。n的扰动对Rz的影响最大，尤其是当n减小时，Rz明显减少，这是由于n减小后相同体积含水率下的土壤吸力明显增大，入渗速率减小，土壤水分运动减慢。此外，θs减小时入渗速率下降，但是土壤可含蓄的水量减小，因此Rz增加。VG模型各参数扰动对Rz的影响见图1。

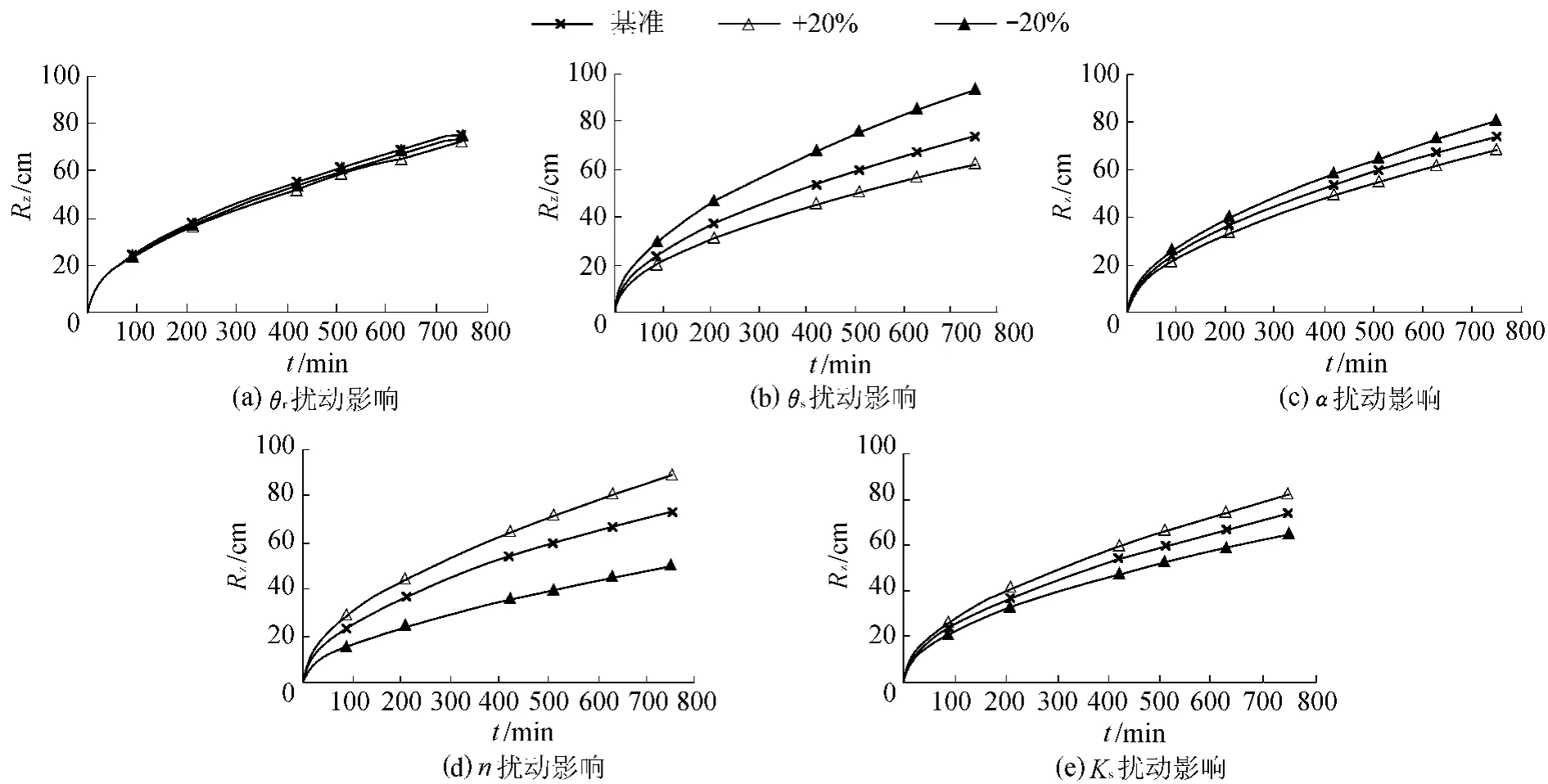
图1 VG模型参数扰动对R z的影响Fig.1 Influence of perturbation of VG model parameters on R z

Rz与入渗历时t可采用单参数幂函数拟合，对于粉壤土，采用式(4)拟合［11］:

式中m为拟合参数。式(4)拟合的结果见表1。

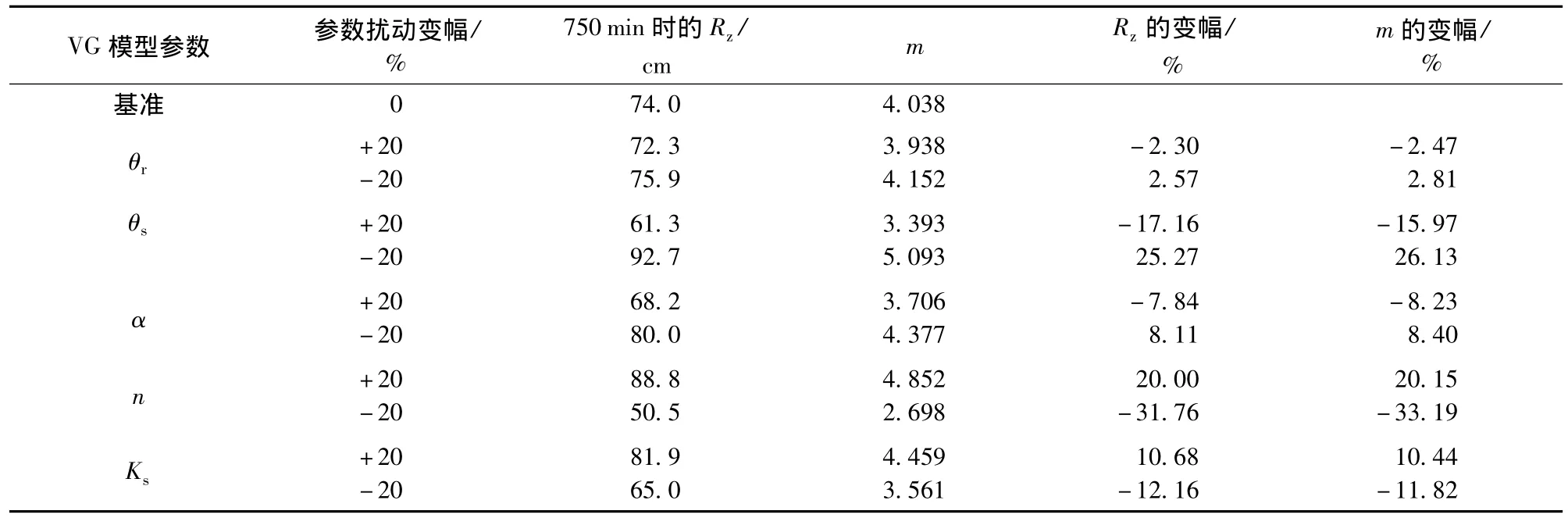
表1 VG模型参数扰动对R z，m的影响Table 1 Influence of perturbation of VG model parameters on R z and m

θs，n和Ks的扰动对Rz及m的影响较大，且Rz和m的扰动变幅均超过了10.00%;α的扰动影响较小，Rz和m的扰动变幅最大值分别为8.11%和8.40%;θr扰动影响最小，Rz和m的扰动变幅不足3.00%;n的负扰动影响最大，Rz和m的扰动变幅分别为-31.76%，-33.19%。

2.2 累计入渗量计算值

θs，n和Ks的扰动均与累计入渗量计算值I呈正相关关系，且n的扰动对I的影响最大;α的扰动与I呈负相关关系;θr的扰动基本不影响I。各参数的扰动对I的影响见图2。

为了定量分析VG模型各参数的扰动对I影响，采用Philip入渗公式进行拟合:

式中S为渗吸系数，cm/min0.5。VG模型各参数扰动对I及Philip公式中渗吸系数的影响结果见表2。

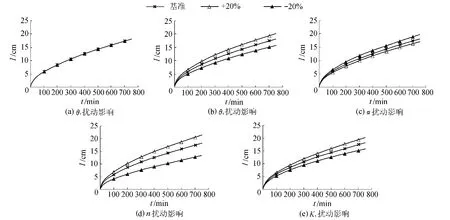
图2 VG模型参数扰动对累计入渗量计算值的影响Fig.2 Influence of perturbation of VG model parameters on calculated values of cumulative infiltration

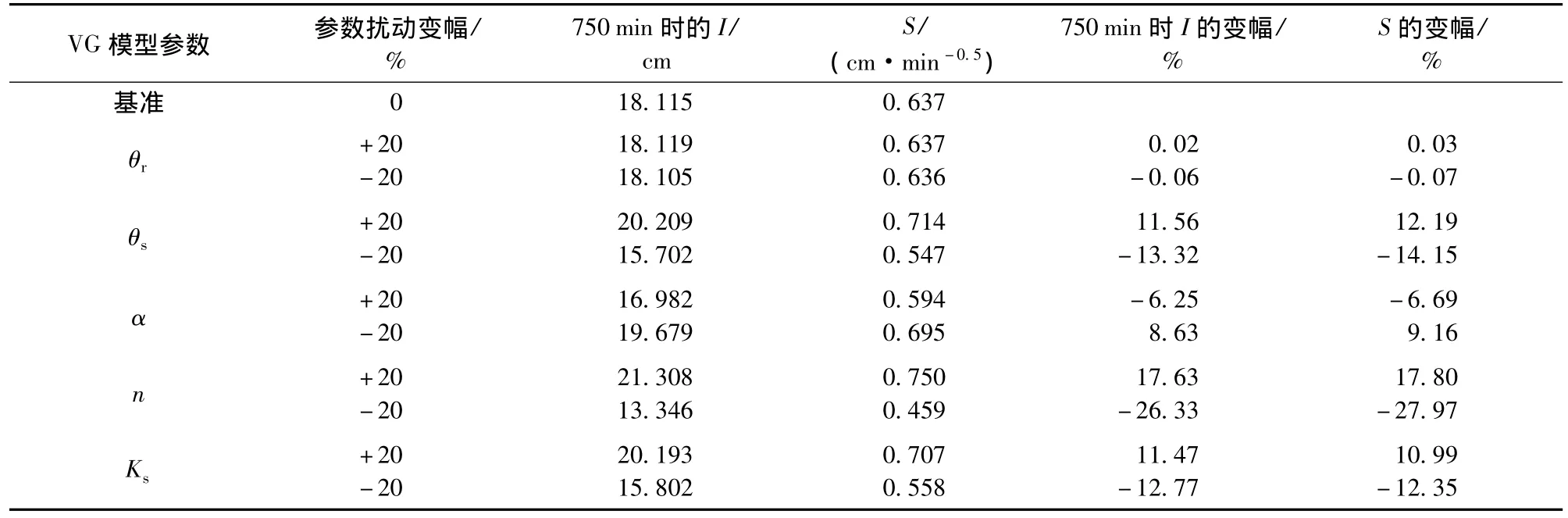
表2 VG模型参数扰动对I及S的影响Table 2 Influence of perturbation of VG model parameters on I and S

结果表明，θs，n和Ks的扰动对I及Philip公式中S的影响较大，I和S的变幅均在10.00%以上;α的扰动对I及S的影响较小，I和S的变幅在-6.69% ～9.16%之间;θr的扰动影响最小，I和S的变幅均低于0.10%，可忽略不计。由模拟结束时刻(750 min)的I可知，n的正、负扰动对其影响最大，I的变幅分别为17.63%和-26.33%;其次是θs，在其扰动下I的变幅分别为11.56%和-13.32%;Ks扰动下，I的变幅为11.47%和-12.77%。VG模型各参数n，θs，Ks，α，θr的扰动对S的影响依次减弱。n的负扰动对S的影响最大，S的变幅为-27.97%。

3 结 论

a.n，θs和Ks的扰动对Rz和I的影响均较大，模拟结束时Rz和I的扰动影响均不低于10%，且对Rz，I模型参数的扰动影响也超过了10%;α的扰动影响次之;θr的扰动影响最小。

b.n值的负扰动对Rz和I的影响最大，且n偏小时对模拟结果带来的误差较大。因此，在实际应用中应保证VG模型参数n，θs，Ks等的精度。

［1］雷志栋，杨师秀，谢森传.土壤水动力学［M］.北京:清华大学出版社，1988.

［2］徐绍辉，刘建立.土壤水力性质确定方法研究进展［J］.水科学进展，2003，14(4):394-401.(XU Shaohui，LIU Jianli.Advances in approaches for determining unsaturated soil hydraulic properties［J］.Advances in Water Science，2003，14(4):394-401.(in Chinese))

［3］刘建立，徐绍辉，刘慧.估计土壤水分特征曲线的间接方法研究进展［J］.水利学报，2004，35(2):68-76.(LIU Jianli，XU Shaohui，LIU Hui.A review of development in estimating soil water retention characteristics from soil data ［J］.Journal of Hydraulic Engineering，2004，35(2):68-76.(in Chinese))

［4］李峰，缴锡云，李盼盼，等.田间土壤水分特征曲线参数反演［J］.河海大学学报:自然科学版，2009，37(4):373-377.(LI Feng，JIAO Xiyun，LI Panpan，et al.Parametric inversion of soil water characteristic curves of farmland［J］.Journal of Hohai University:Natural Sciences，2009，37(4):373-377.(in Chinese))

［5］吕殿青，邵明安.非饱和土壤水力参数的模型及确定方法［J］.应用生态学报，2004，15(1):163-166.(LYU Dianqing，SHAO Ming'an.Models and determining methods of unsaturated soil hydraulic parameters［J］.Chinese Journal of Applied Ecology，2004，15(1):163-166.(in Chinese))

［6］卢小慧，靳孟贵，汪丙国.栾城农业生态系统试验站土壤水分特征曲线分析［J］.中国农村水利水电，2006(12):30-32.(LU Xiaohui，JIN Menggui，WANGBingguo.Discussion on the soil water characteristic curve of the agricultural eco-system experiment station in Luancheng，Hebei Province［J］.China Rural Water and Hydropower，2006(12):30-32.(in Chinese))

［7］GENUCHTEN M T.A closed-form equation for predicting the hydraulic conductivity of unsaturated soils［J］.Soil Sci Soc Am J，1980，44(5):892-898.

［8］刘毅，陈吉宁，杜鹏飞.环境模型参数识别与不确定性分析［J］.环境科学，2002，23(6):6-10.(LIU Yi，CHEN Jining，DU Pengfei.Parameters identification and uncertainty analysis for environmental model［J］.Environmental Science，2002，23(6):6-10.(in Chinese))

［9］田雨，雷晓辉，蒋云钟，等.水文模型参数敏感性分析方法研究评述［J］.水文，2010，30(4):9-12.(TIAN Yu，LEI Xiaohui，JIANG Yunzhong，et al.Comment on parameter sensitivity analysis of hydrological model［J］.Journal of China Hydrology，2010，30(4):9-12.(in Chinese))

［10］聂卫波.畦沟灌溉水流运动模型与数值模拟研究［D］.杨凌:西北农林科技大学，2009.

［11］聂卫波，马孝义，王术礼.一维土壤入渗特性数值模拟［J］.灌溉排水学报，2009，28(3):53-57.(NIE Weibo，MA Xiaoyi，WANG Shuli.Numerical simulation of one-dimensional soil infiltration characteristic ［J］.Journal of Irrigation and Drainage，2009，28(3):53-57.(in Chinese))

［12］毕经伟，张佳宝，陈效民，等.农田土壤中土壤水渗漏与硝态氮淋失的模拟研究［J］.灌溉排水学报，2003，22(6):23-26.(BI Jingwei，ZHANG Jiabao，CHEN Xiaomin，et al.Modeling of soil water erainage and nitrate leaching in arable soils［J］.Journal of Irrigation and Drainage，2003，22(6):23-26.(in Chinese))

［13］孟江丽.水盐和排水系统的模拟研究［D］.乌鲁木齐:新疆农业大学，2004.

［14］梁冰，姜利国.非饱和带水分运动模型的Picard解法及参数灵敏度分析［J］.水资源与水工程学报，2009，20(5):23-27.(LIANG Bing，JIANG Liguo.Picard solution of moisture movement model in unsaturated zone and parameter sensitivity analysis［J］.Journal of Water Resources＆ Water Engineering，2009，20(5):23-27.(in Chinese))

［15］ŠIMUNEK J，ŠEJNA M，SATIO H，et al.The HYDRUS-1D software package for simulating the one-dimensional movement of water，heat，and multiple solutes in variably-saturated media［M］.Version 4.California:U.S.Salinity Laboratory，2008.

［16］SCHAAP M G，LEIJ F J.Using neural networks to predict soil water retention and soil hydraulic conductivity［J］.Soil and Tillage Research，1998，47(1/2):37-42.

［17］魏义长，刘作新，康玲玲.辽西淋溶褐土土壤水动力学参数的推导及验证［J］.水利学报，2004，35(3):81-86.(WEI Yichang，LIU Zuoxin，KANG Lingling.Derivation and verification of soil hydrodynamic parameters in cinnamon soil［J］.Journal of Hydraulic Engineering，2004，35(3):81-86.(in Chinese))