混凝土连续梁桥人字形高桥墩分岔区横梁局部应力分析

张亮亮，杨建新，黄 瑜，王永杰

(1.重庆大学土木工程学院，重庆 400045;2.澧县住房和城乡建设局，湖南常德 415500;3.重庆中海投资有限公司，重庆 408400;4.中国航天建设集团有限公司，北京 100071)

为跨越沟壑、满足线路标高、节约墩身圬工量，某山区铁路桥采用高139 m的人字形超高桥墩(图1)。文献［1-4］已对异型桥墩进行了应力状况分析，但笔者研究的桥墩在下部岔区设有1根横梁连接左右墩柱，横梁为空心矩形混凝土梁，墩柱内部为实体，岔区横梁及其附近墩柱受力情况更为复杂［5-8］，因此有必要对桥墩分岔区节点进行局部空间应力分析。为准确获取岔区横梁及其附近墩柱在不同工况下的受力情况，了解该区域应力分布规律，确保这种超高墩结构安全、可靠，笔者采用ANSYS软件对此区域进行空间应力分析。

1 工程概况

某山区铁路桥主桥为刚构-连续组合梁，跨径为(80+3×144+80)m。梁体采用单箱单室、变高度、变截面箱梁，箱梁宽11 m，桥墩处梁高11 m，跨中合龙段箱梁高6 m，其余梁段梁底下缘按二次抛物线变化。12～14号桥墩为人字形墩，采用墩梁固结法连接;13号桥墩上部65m为变截面矩形空心墩，然后经过5m高实体桥墩进入岔区，在岔区设置一根高5m、宽8m、壁厚1m的空心横梁，在横梁高度范围墩柱内部采用实心。

2 有限元模型

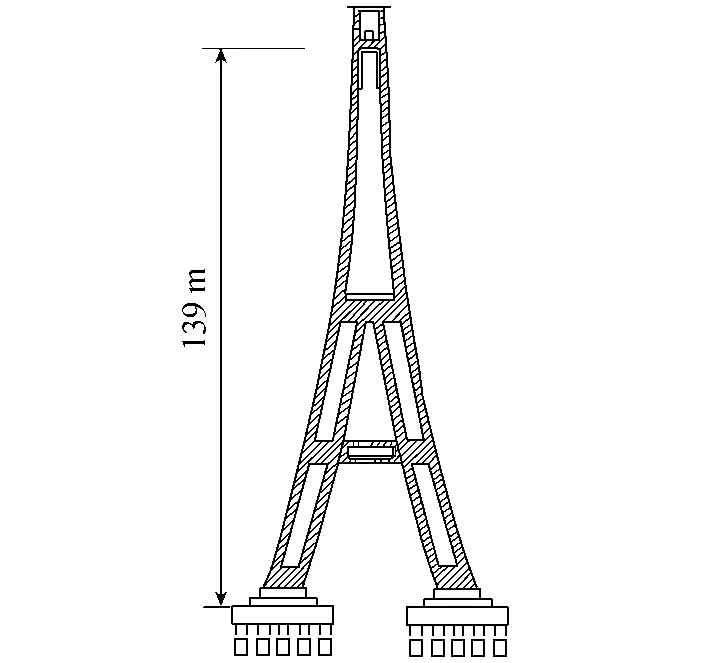
图1 13号桥墩横断面示意图Fig.1 Sketch map of cross section of bridge pier No.13

2.1 模型建立

铁路桥全桥有限元模型如图2所示，主梁采用BEAM189单元模拟，桥墩采用三维20节点实体单元SOLID95模拟［9-10］。在墩梁节点连接处通过建立刚域来模拟主梁与桥墩的连接，球形支座处通过约束梁单元节点的横向和竖向位移来模拟，墩底承台设置为固结。

为准确反映岔区横梁及附近墩柱部分的应力情况，笔者采用ANSYS软件中的切割边界方法［11］进行岔区节点区子模型的提取。切割边界就是子模型从整个较粗糙的模型分割开的边界，整体模型切割边界的计算位移值即为子模型的边界条件，然后对子模型进行更密的网格划分得到合理的分析结果，岔区节点区有限元子模型如图3所示。

2.2 荷载工况

按照TB10002.1—2005《铁路桥涵设计基本规范》的要求选取桥墩应力分析时外部荷载工况，如表1所示。

图2 全桥有限元模型Fig.2 FEM model of whole bridge

表1 桥梁应力分析荷载工况Table 1 Load conditions for stress analysis of bridge pier

图3 岔区节点区有限元子模型Fig.3 FEM sub-model of bifurcation region

3 岔区节点区及横梁应力计算结果与分析

3.1 岔区节点区应力计算结果

在工况3荷载下，岔区节点区主压、主拉应力云图如图4所示。图4(a)中最大主压应力为7.57 MPa，位于墩柱内实体与墩柱内壁交接处;横梁下部的主压应力最小，墩柱外侧主压应力较大，最大值出现在横梁和墩柱交界处。图4(b)中最大主拉应力为1.97 MPa，横梁下部主拉应力较大，墩柱主拉应力较小，在墩柱范围内拉应力值变化很小。其他3种工况下，横梁处的应力分布趋势基本相同，只是最大值不同。

3.2 横梁应力计算结果

在工况3荷载作用下横梁受力情况最不利，其应力云图如图5所示。由于桥墩承受的自重和上部荷载主要通过墩柱传递，墩柱主压应力较大，而在墩柱内部的实体部分主压应力较小。在横梁与墩柱的交界处，由于构造上的突变，产生拉应力集中。横梁底部拉应力较大，在墩柱内部实体与内壁的交界处出现最大拉应力，数值为1.97 MPa。

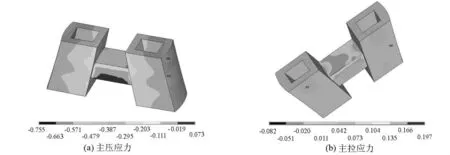
图4 岔区节点区在工况3下的应力云图(单位:107 MPa)Fig.4 Stress distribution of bifurcation region in load case 3(units:107 MPa)

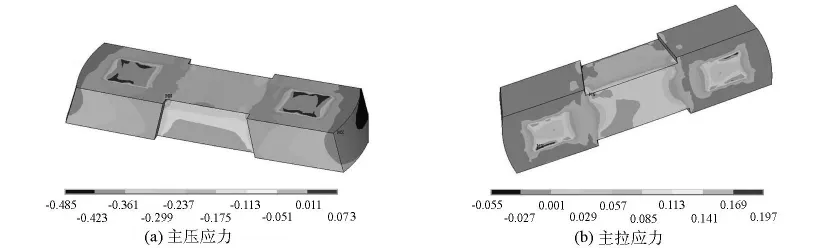
图5 横梁在工况3下的应力云图(单位:107MPa)Fig.5 Stress distribution of cross beam in load case 3(units:107 MPa)

通过分析4种工况下子模型的空间应力，可得:(a)总体来看，子模型2个分岔的空心墩从桥墩的中心轴向外侧受到的主压应力越来越大。(b)最大主压应力和最大主拉应力分别为7.57 MPa和1.97 MPa。主压应力基本不超过5.73MPa，其仅在横梁与墩柱壁内、外表面的交界处因为应力集中而比较大。(c)在空心墩内部的横梁混凝土的主压应力水平很低，范围为0.11～0.51MPa。最大主拉应力为1.97 MPa，位于该处混凝土下表面，靠近墩柱内壁处。结果表明，最大应力均满足规范规定，该铁路桥下部岔区横梁与墩柱的连接是安全、可靠的。

4 不同构造形式横梁下子模型的应力分布

为了得到合理的横梁构造形式，分别设置不同的横梁高度、宽度和壁厚，在工况3下分别计算子模型的应力分布，如图6所示。

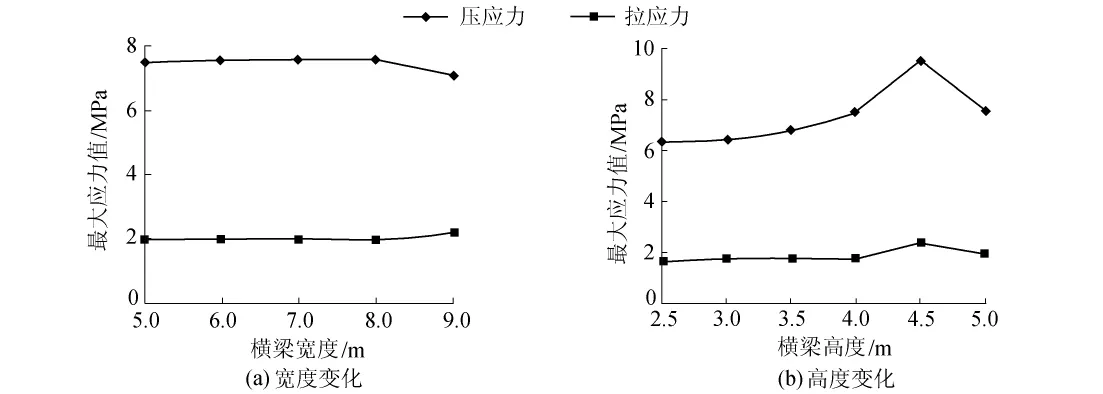
图6 横梁构造变化对应力分布的影响Fig.6 Influence of different structures on stress of cross beam

结果表明，在横梁宽度变化时，横梁区应力分布规律变化很小(图6(a))。改变横梁宽度对下部节点处的应力水平影响很小，但横梁宽度取为8.0 m时，最大主拉应力和节点中间截面底缘纵向主拉应力偏小，因此横梁宽度为8.0 m时最合理。图6(b)表明，随着横梁高度的增加应力呈增大趋势，且各种情况下的最大应力水平都是安全的;当横梁高度变化到4.5 m时，子模型的主压应力和主拉应力最大，主压应力达到9.50 MPa，主拉应力达到2.36 MPa。如果横梁在桥墩竖向的位置不变，适当减小横梁高度对横梁的受力是有利的。但横梁高度的设置还要综合考虑地震作用和桥墩的稳定性，其尺寸不能太小。为了确保节点不成为地震作用下结构的薄弱环节，建议采用横梁高度为5.0 m。横梁壁厚对于主应力的影响不显著，计算结果表明，壁厚1.0 m时最大主拉应力最小。

5 人洞应力集中分析

横梁两端的墩柱内部为实体，其中心需要设置洞口并埋置检查梯。为了得到合理的开洞方式，笔者分别计算了6种开洞方案下的应力分布(方案1:80 cm×80 cm矩形洞口;方案2:80 cm×80 cm矩形洞口加10 cm×10 cm倒角;方案3:80 cm×80 cm矩形洞口加半径15 cm圆弧倒角;方案4:80 cm×80 cm矩形洞口加15 cm×15 cm倒角;方案5:80 cm×80 cm矩形洞口加20 cm×20 cm倒角;方案6:直径80 cm的圆形)，计算中荷载采用桥墩顶轴力最大时的荷载组合(工况2)。

因为6种开洞方案洞口附近都没有出现主压应力集中现象［12］，因此只需要考虑洞口附近的主拉应力分布情况。方案1～6的洞口附近混凝土的主拉应力最大值依次为2.45 MPa，3.14 MPa，2.67 MPa，2.36 MPa，2.05 MPa，1.60 MPa。矩形人洞角点处附近的应力集中相当严重，在角点处设置倒角后结构突变减弱，应力集中现象也相应减少;随着倒角的增大，角点处的应力分布更均匀，倒角的设置能有效减少应力集中。设置圆形人洞时应力分布更均匀，且应力集中现象最弱，洞口附近主拉应力值最小。

6 结 语

人字形桥梁岔区横梁与墩柱连接处的空间受力特性复杂，简化分析不能较详细地把握其受力状况，因此对其进行空间应力分析很必要。笔者通过分析某山区铁路桥在各种工况下该区域的应力分布状况，发现岔区节点区最大主压应力和最大主拉应力均小于规范限值;通过比较不同构造形式横梁下的空间应力，认为横梁宽8.0 m、高5.0 m、壁厚1.0 m时的应力分布比较合理;通过对比不同人洞开洞方案下的洞口角点应力集中现象，得出圆形人洞可以有效减小洞口的应力集中的结论。

［1］王慧东.桥梁墩台与基础工程［M］.北京:中国铁道出版社，2005:64-75.

［2］葛俊颖.桥梁工程(上)［M］.北京:中国铁道出版社，2010:305-317.

［3］蔡德强.广珠城际轨道实体桥墩设计分析［J］.桥梁建设，2010(2):49-51.(CAI Deqiang.Design and analysis of solid pier for bridge on Guangzhou-Zhuhai intercity railway transit［J］.Bridge Construction，2010(2):49-51.(in Chinese))

［4］许智焰，马庭林.内昆铁路花土坡特大桥设计［J］.桥梁建设，2004(1):31-33.(XU Zhiyan，MA Tinglin.Design of Huatupo Bridge on Neijiang-Kunming railway［J］.Bridge Construction，2004(1):31-33.(in Chinese))

［5］葛素娟，李静斌.预应力混凝土连续刚构桥0号块空间分析［J］.郑州大学学报:工学版，2006，27(3):1-5.(GE Sujuan，LI Jingbin.Spatial analysis of segment No.0 of prestressed concrete continued rigid frame bridge［J］.Journal of Zhengzhou University:Engineering Science，2006，27(3):1-5.(in Chinese))

［6］夏勇，裴若娟.广珠准高速铁路东海西江大0号块空间分析［J］.桥梁建设，1997(4):74-77.(XIA Yong，PEI Ruojuan.Spatial analysis of segment No.0 of Donghai Xijiang River bridge of Guangzhou-Zhuhai quasi-high-speed railway［J］.Bridge Construction，1997(4):74-77.(in Chinese))

［7］王砺文.大跨连续刚构墩梁固接处的空间应力分析［J］.铁道标准设计，2003(8):36-38.(WANG Liwen.Analysis of spatial stress at the joint between piers and beams in a large-span continuous rigid-frame bridge［J］.Railway Standard Design，2003(8):36-38.(in Chinese))

［8］何海，王荣辉.混凝土连续梁桥空心墩墩顶局部应力分析［J］.城市道桥与防洪，2004(4):60-63.(HE Hai，WANG Ronghui.Analysis of partial stress at hollow pier top of concrete continuous beam bridge［J］.Urban Roads ＆ Flood Control，2004(4):60-63.(in Chinese))

［9］王勖成.有限单元法［M］.北京:清华大学出版社，2003:105-127.

［10］谢肖礼，彭文立，秦荣.圣维南原理在钢管混凝土拱桥分析中的应用［J］.中国公路学报，2001，14(2):33-35.(XIE Xiaoli，PENG Wenli，QIN Rong.Application of SAINT-VENANT principle in analysis of CFST arch bridge［J］.China Journal of Highway and Transport，2001，14(2):33-35.(in Chinese))

［11］王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2007:275-280.

［12］徐芝纶.弹性力学简明教程［M］.北京:高等教育出版社，2002:67-72.