综合误差系数在新安江模型参数全局优化中的应用

叶金印，姚 成，李京兵，李致家

(1.河海大学水文水资源学院，江苏南京 210098;2.淮河流域气象中心，安徽蚌埠 233040;3.安徽省水文局，安徽合肥 230022)

流域水文模型作为一种研究流域内复杂水文现象的重要工具，一直是水文学研究的热点。而在进行模型应用时，如何确定合理可靠的模型参数，往往是需要解决的首要问题。随着计算机技术与现代数学方法的发展，模型参数的率定方法正逐渐由人工试错法向自动优化方法转变，大量的优化算法被引入到水文模型的参数率定中。其中，SCE-UA算法作为一种具有代表性的单目标全局优化算法，得到了广泛的应用和研究。已有的研究成果［1-2］表明，在将该算法用于模型参数率定时，目标函数的选取往往制约着寻优结果，进而影响模型的应用效果。现有常用的目标函数一般都是以单个精度评定指标为主，这样会导致模型的模拟结果对该指标对应的误差控制较好，然而却忽略了对其他指标的考虑，使模型不能全面地反映流域的水文过程。

笔者以径流深相对误差、洪峰相对误差、峰现时差与确定性系数4个精度评定指标为基础，采用综合误差系数的方法为SCE-UA算法构建了考虑多因素的单目标函数，并将其应用于新安江模型的参数率定，以皖南山区芦溪流域为例，进一步开展新安江模型参数的全局优化研究。

1 新安江模型简介

新安江模型作为一个概念性模型，自建立以来就得到了广大学者的认同，在中国的洪水预报中得到广泛应用，并取得良好的应用效果［3-6］。在采用新安江模型进行水文模拟时，首先要根据降水和下垫面特征将流域划分为若干个单元，然后对每个单元分别进行产汇流计算，得到单元流域的出流过程，最后将其演算至流域出口并进行叠加，即可得到整个流域的出流过程。该模型由4个模块组成，即蒸散发模块、产流模块、分水源模块、汇流模块，每个模块分别对应不同的模型参数［3-4］。

2 SCE-UA算法

SCE-UA算法是一种有效解决非线性约束最优化问题的方法，能够根据单目标函数快速搜索到全局最优解，可以解决高维参数的全局优化问题。该算法的基本思路是将基于确定性的复合形搜索技术与自然界中的生物竞争进化原理相结合，用来求解最小化问题。其融合了确定性方法、随机性方法、竞争进化、复合形混合等概念，从而保证SCE-UA算法搜索的灵活性、有效性等。随着对SCE-UA算法研究的深入，该算法在流域水文模型参数优化中的应用日趋广泛，被认为是水文模型参数优化中最有效的方法之一［7-10］。SCE-UA算法的参数虽然较多，但绝大部分取值都可以采用已有研究成果的默认值。应用该算法时，一般包括初始化、产生样本点、样本点排序、划分复合形群体、复合形进化、复合形混合及收敛性判断7个步骤［2，7-9］。

当采用SCE-UA算法进行水文模型参数率定时，目标函数的选取对率定结果有显著影响，不同的目标函数往往会得到不同的优化结果。为了使SCE-UA算法中单一的目标函数能够较全面地描述由实测资料所反映的水文特征，笔者采用综合误差系数(CEC)方法:

式中:Ei——任意一个独立的误差或精度评定指标;n——评定指标的个数。例如，对于洪水过程而言，采用GB/T 22482—2008《水文情报预报规范》［11］中的径流深相对误差(RRE)、洪峰相对误差(RPE)、峰现时差(PTE)以及确定性系数(DC)作为精度评定指标，则 n=4，E1=EP，E2=EPT，E3=ER，E4=EDC。其中［12］

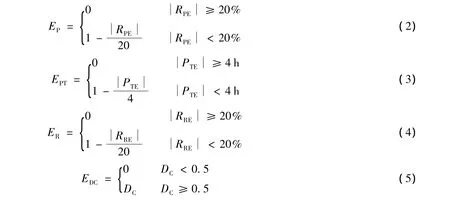
对于日径流过程，考虑到对于峰值和峰现时间要求不高，可以只采用RPE与DC作为精度评定指标，则n=2，E1=EP，E2=EDC。

由CEC的算法可以看出该系数值介于0～1之间，CEC值越大则表明模型计算结果越好，反之则表明模型计算结果越差。因此，目标函数可定义为

3 研究流域概况

选用位于皖南山区的芦溪流域作为研究流域，流域面积为992 km2。该流域植被良好，雨量充沛，多年平均降雨量约为1830 mm，为典型的湿润流域。芦溪流域地势北高东低，最大、最小以及平均海拔高程分别为1576 m，61 m，285 m，相对高差较大，河道平均坡度为0.17%。该流域降雨在年内、年际分配极不均匀，汛期内的降雨量一般占年总降雨量的60%以上。芦溪流域水系及雨量站分布见图1。

4 应用结果分析

选用芦溪流域1965—2006年共计42 a日径流过程，以及资料现有的全部18次洪水摘录过程进行模型参数率定及检验。其中，前30 a的日径流资料与前13次洪水过程分别用于新安江日模型与次洪模型的参数率定，其余资料用于模型的参数检验。在采用SCE-UA算法进行参数率定时，对于日模型而言，综合误差系数分别考虑了3种情况:ER，EDC以及ER+EDC;对于次洪模型而言，RPE与 PTE作为必须考虑的2个评定指标，因此综合误差系数分别考虑了4种情况:EP+EPT，EP+EPT+ER，EP+EPT+EDC以及 EP+EPT+ER+EDC。针对以上各种情况，基于综合误差系数方法，分别进行模型参数率定及检验。表1为新安江模型模拟率定期与检验期内所有出流过程结果的误差统计。由于日模型计算结果对RPE与PTE指标的要求相对较低，因此表1中的日径流过程模拟未对这2个指标进行统计。

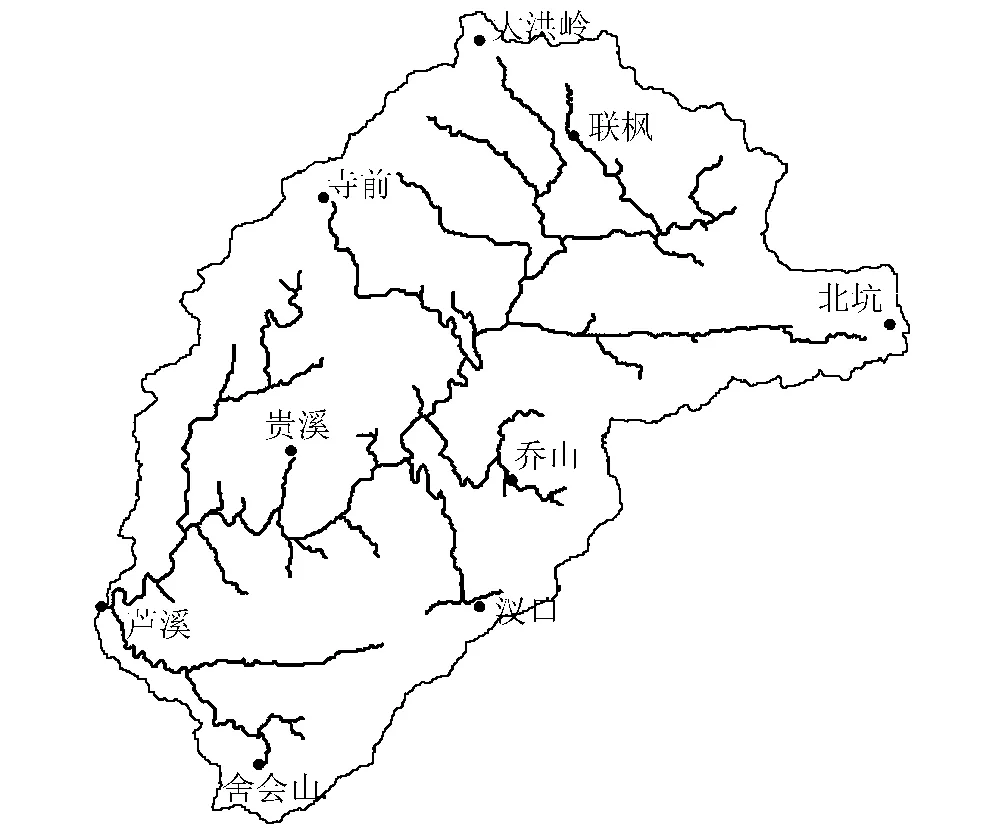
图1 芦溪流域水系及雨量站分布示意图Fig.1 Sketch map of drainage network and locations of gauge stations of Luxi Basin

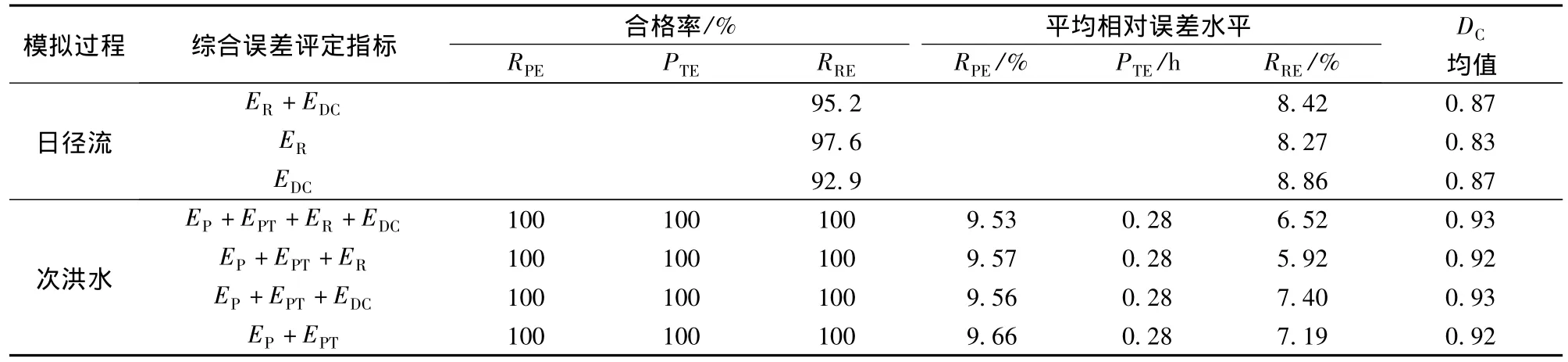
表1 基于综合误差系数方法的新安江模型模拟结果误差统计Table 1 Accuracy statistics of Xin’anjiang model simulation results based on comprehensive error coefficient method

图2、图3分别为日径流模拟结果与次洪模拟结果统计箱形图，描述了各个精度统计结果的最大值、上四分位数、中位数、下四分位数及其最小值。图4为摘录的2000年日径流过程与2次洪水过程线比较。

由表1与图2～4可以看出，采用SCE-UA算法率定的模型参数，模型能够很好地模拟芦溪流域的水文过程。对于日模型而言，在目标函数内考虑单个指标，如RRE或DC，可以使模拟结果对该指标控制最好，但考虑多个指标，可以使模拟结果的整体效果最好。通过对次洪模型应用结果的分析，也可以得到相同的结论。因此，为了更准确地模拟流域的水文过程，在进行新安江模型参数优化时用于日模型的综合误差系数建议同时采用RPE与DC作为评定指标，用于次洪模型的综合误差系数建议同时采用RPE，PTE，RRE及DC作为评定指标。

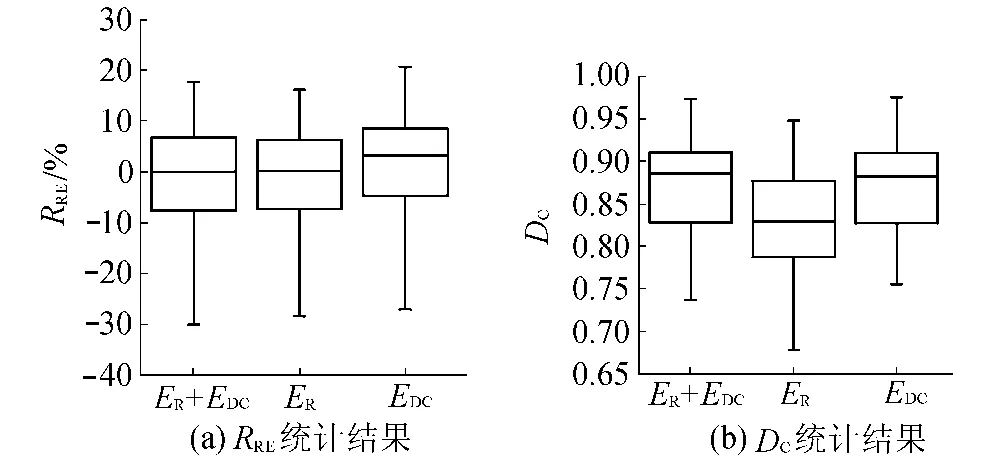
图2 新安江日模型模拟结果R RE与D C统计箱形图Fig.2 Box plots of R RE and D C statistics for daily simulation with Xin’anjiang model

5 结 语

在采用单目标全局优化算法率定水文模型参数时，选取合理而全面的目标函数对于模型应用效果十分重要。笔者基于4个精度评定指标RRE，RPE，PTE和DC，针对SCE-UA算法，利用综合误差系数的方法构建目标函数，并以此为基础率定新安江模型的参数，取得良好的效果。分析结果表明，在目标函数中选取不同的精度评定指标将对模型的模拟结果造成影响。采用综合误差系数可以使单一的目标函数考虑单个或多个指标，能够较全面地考虑各个指标对模拟结果的影响。在目标函数中考虑多个指标能使模拟精度整体上达到最优，每个指标的特征值可得到较好的控制，从而获取更可靠的模型参数。本文暂没有考虑不确定性、异参同效等现象对于参数优化结果的影响，相关问题还有待进一步的深入研究。

图3 新安江次洪模型模拟结果R PE，R RE与D C统计箱形图Fig.3 Box plots of R PE，R RE，and D C statistics for hourly flood simulation with Xin’anjiang model

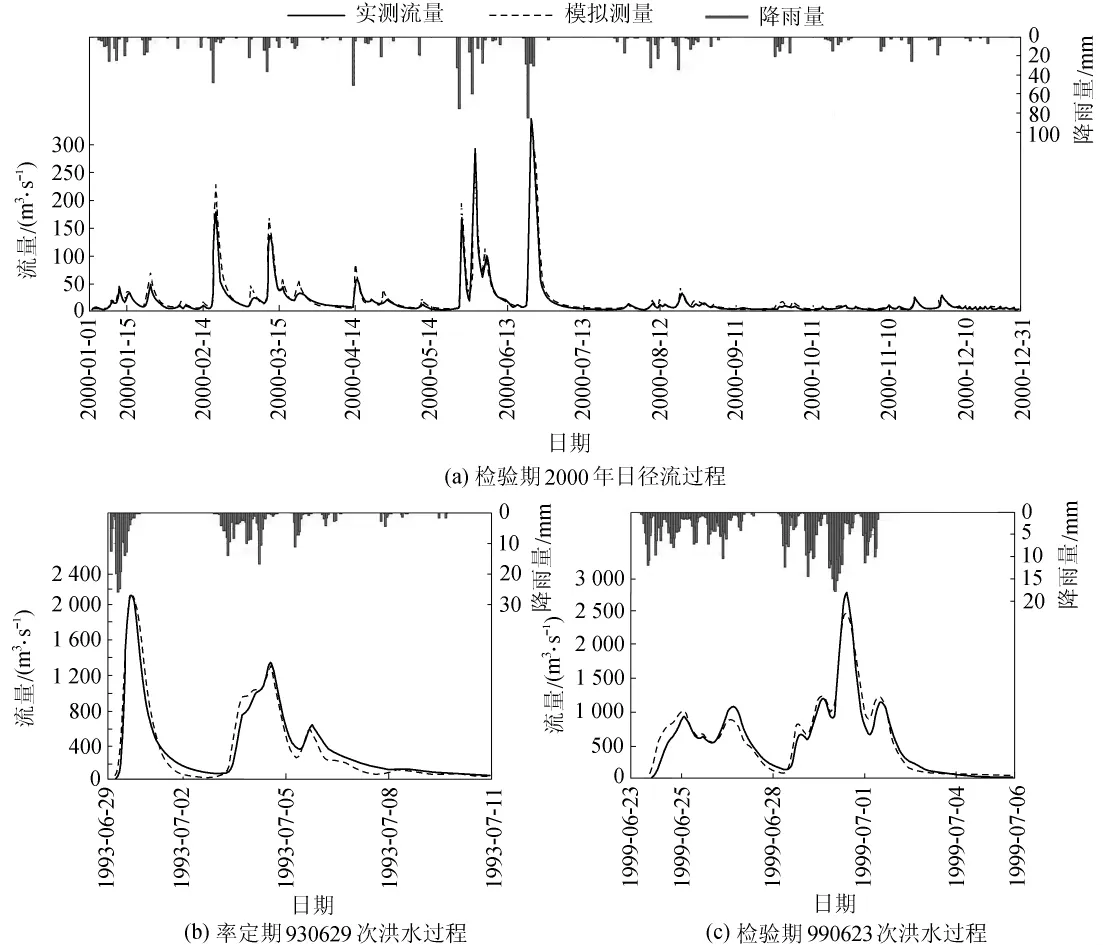
图4 新安江模型模拟过程线Fig.4 Simulated results of Xin’anjiang model

［1］DUAN Q，SOROOSHIAN S，GUPTA V.Effective and efficient global optimization for conceptual rainfall-runoff models［J］.Water Resource Research，1992，28(4):1015-1031.

［2］DUAN Q，SOROOSHIAN S，GUPTA V.Optimal use of the SCE-UA global optimization method for calibrating watershed models［J］.Journal of Hydrology，1994，158:265-284.

［3］赵人俊.流域水文模拟［M］.北京:水利电力出版社，1984.

［4］ZHAO R，LIU X.The Xin’anjiang model［C］//SINGH V.Computer models of watershed hydrology.Colorado:Water Resources Publications，1995:215-232.

［5］姚成，纪益秋，李致家，等.栅格型新安江模型的参数估计及应用［J］.河海大学学报:自然科学版，2012，40(1):42-47.(YAO Cheng，JI Yiqiu，LI Zhijia，et al.Parameter estimation and application of grid-based Xin’anjiang model［J］.Journal of Hohai University:Natural Sciences，2012，40(1):42-47.(in Chinese))

［6］叶金印.基于气象观测雨量资料的实时洪水预报模型应用研究［D］.南京:南京大学，2007.

［7］李致家.水文模型的应用与研究［M］.南京:河海大学出版社，2008.

［8］李致家，周轶，哈布哈其.新安江模型参数全局优化研究［J］.河海大学学报:自然科学版，2004，32(4):376-379.(LI Zhijia，ZHOU Yi，HAPUARACHCHI H.Application of global optimization to calibration of Xin’anjiang model［J］.Journal of Hohai University:Natural Sciences，2004，32(4):376-379.(in Chinese))

［9］戴健男，李致家，黄鹏年，等.新安江模型参数不确定性分析［J］.河海大学学报:自然科学版，2011，39(6):618-622.(DAI Jiannan，LI Zhijia，HUANG Pengnian，et al.Uncertainty analysis of Xin’anjiang model parameters［J］.Journal of Hohai University:Natural Sciences，2011，39(6):618-622.(in Chinese))

［10］宋星原，舒全英，王海波，等.SCE-UA、遗传算法和单纯形优化算法的应用［J］.武汉大学学报:工学版，2009，42(1):6-9.(SONG Xingyuan，SHU Quanying，WANG Haibo，et al.Comparison and application of SCE-UA，genetic algorithm and simplex method［J］.Engineering Journal of Wuhan University，2009，42(1):6-9.(in Chinese))

［11］GB/T 22482—2008 水文情报预报规范［S］.

［12］姚成.基于栅格的新安江(Grid-Xinanjiang)模型研究［D］.南京:河海大学，2009.