岩石单裂隙渗流-传热模型及其参数敏感性分析

董海洲，罗日洪，张 令

(1.河海大学地球科学与工程学院，江苏南京 210098;2.河海大学岩土工程研究所，江苏南京 210098)

裂隙岩石渗流-传热问题常包含瞬态、非均质等复杂过程，很难得到其解析解，一般采用数值计算方法来进行模拟［1］。但在特定情况下，可以通过简化模型得到半解析解或解析解。简化模型的特点是概念简单明了，方便用于分析裂隙渗流-传热的基本特征以及一些影响参数的敏感性。

鉴于裂隙岩石渗流的复杂性，一般将其简化为单裂隙平板模型进行研究。例如Lauwerier等［2-4］分别提出了不同的简化概念模型和解析解;柴军瑞等［5-6］分别对单裂隙非稳定流进行了分析，并进行岩石一维渗流场与温度场的耦合分析，得出模型的近似解析解;张文捷等［7］建立了改进的离散-连续介质岩石渗流耦合模型，提出反映水头间断程度的连续系数概念;孙粤琳等［8］研究了瞬态温度场作用下岩体表面裂缝的扩展，表明温度场对岩体裂缝的扩展有很大的影响。

热源法可用于岩石中单裂隙渗流-传热机制的研究。笔者借鉴非稳态平面热源法中的传热数学模型［9］，建立岩石单裂隙在瞬态下的传热数学模型，得到裂隙岩石过余温度的瞬态解析解。在此基础上，分析岩石单裂隙传热的一般规律，以及模型中几个主要参数(裂隙水流速度、隙宽、水流与岩石初始温度差)的敏感性，得到这3个参数对岩石温度场的影响程度。

1 几何模型的建立及求解

几何模型的假定:(a)岩体本身的渗透性忽略不计，地下渗透水流只在岩石裂隙中流动;(b)裂隙内水流为稳定层流，具有常物性、无内热源、不可压缩性，水流温度稳定;(c)岩体内存在单一裂隙，裂隙为平行状窄缝，且无限延伸，裂隙长度远大于隙宽;(d)岩体中的热量传输只考虑热传导，忽略对流换热、热辐射的影响;(e)裂隙无填充。

1.1 几何模型的建立

取微小单裂隙岩体几何模型，单裂隙两边岩体无限大，在无穷远处岩石温度的x方向无限延伸。无穷远处原始地层温度为Ts0，岩石即时温度为Ts。由于单裂隙隙宽很小，近似取单裂隙的隔水边界为y=0。如图1所示，在y方向进行半无限大瞬态导热问题的求解，假设在某一水头差的作用下，单裂隙内的流速是不变的，相应的导热方程、初始条件和边界条件分别为

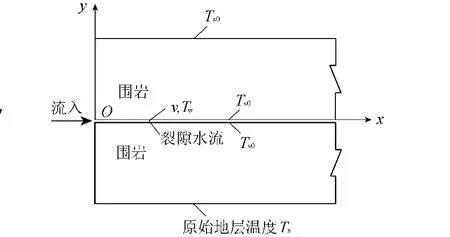
图1 单裂隙热流模型示意图Fig.1 Sketch map of single fracture heat flow model

式中:θ——过余温度，θ＞0对应于岩石受裂隙高温渗透，水流对其产生的温升，θ＜0对应于地热作用下岩石致使裂隙渗透水流温度升高，而岩石本身产生的温降，℃;t——时间，s;y——岩石内部到隔水边界距离，m;as——热扩散率，m2/s;λs——导热系数，W/(m·K);f(t)——边界上施加的热流密度，W/m2。

1.2 几何模型求解

对定解问题(1)中的方程关于t作Laplace变换加以求解，最终可得Laplace空间温度变换的解析解:

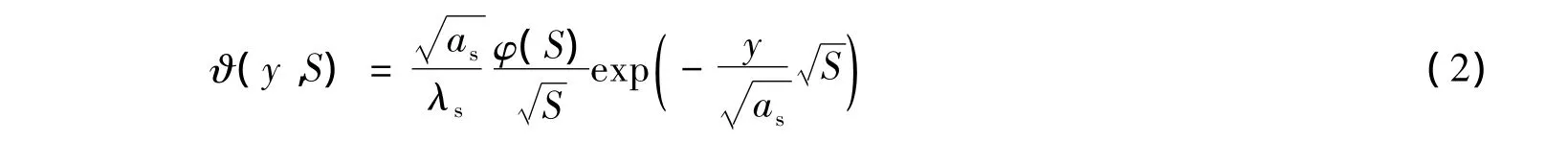
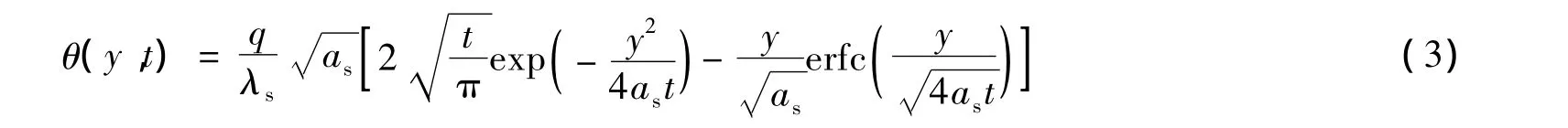
式中erfc(*)为余误差函数。

1.3 热源密度的确定

岩石裂隙中地下水的流动属于受迫对流传热，对流换热量可以根据牛顿冷却定律来计算，则流体吸收的热量为

式中:Tw——流体的温度(Ts＞Tw);A——物体的表面积。则由式(4)可得边界热流密度为

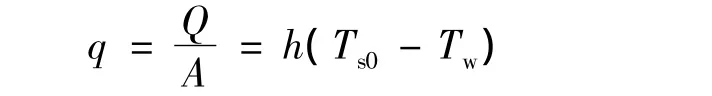
式中:S——Laplace变量;ϑ——θ的 Laplace变换;φ——热流密度 f(t)的 Laplace变换。

经过Laplace逆变换，对于f(t)=q(常数)可得

式中h为岩石与水的热交换系数。

当裂隙水流为层流，则有［10］

其中

式中:Nu——努塞尔数;Re——雷诺数;Pr——普朗特数;L——特征长度，m;λw——水的导热系数，W/(m·℃);Cw——水的比热容，J/(kg·℃);ρw——水的密度，kg/m3;v——水流流速，m/s;μ——水的动力黏滞系数，Pa·s。

综上可得

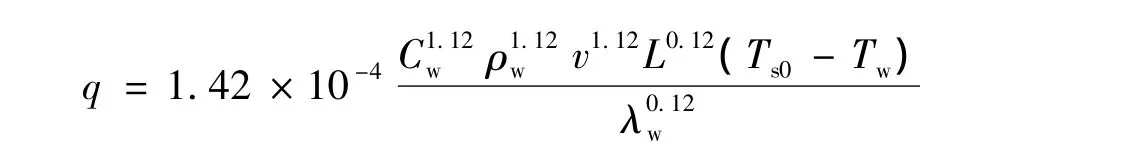
将其代入式(3)，可得裂隙岩石的过余温度模型的解析解:

2 岩石单裂隙传热影响因素分析

地下水在岩石裂隙运动时，忽略温度对渗流的影响，所以假定Cw，ρw，λw，λs，as都为常物性参数，以花岗岩为例，取其工程常用的参数［11］:Cw=4 200 J/(kg·℃)，ρw=1 000 kg/m3，λw=0.6 W/(m·℃)，λs=2.391 W/(m·℃)，as=1.384 ×10-6m2/s。由式(4)可知，过余温度 θ(y，t)与裂隙水流速度 v、隙宽 b、水流与岩石初始温度差ΔT(Ts0-Tw)以及y和t有关。

下面进行不同工况下单裂隙传热数学模型计算，从而分析单裂隙传热影响因素的变化规律。计算中取特征长度为b，裂隙水流速度为v1=5×10-5m/s，v2=4×10-4m/s，v3=10-3m/s;隙宽分别为b1=5×10-6m，b2=1.8×10-5m，b3=5×10-5m;岩石初始温度分别为Ts1=25℃，Ts2=30℃，Ts3=35℃，地下水初始温度为Tw=20℃。

2.1 过余温度随t和y的变化规律

距离隔水边界越近，温度场变化越剧烈。图2(a)为沿y方向一簇不同y值下，θ与t的关系曲线。各条曲线的变化速率开始时比较快，然后变缓，最后趋于零。图2(b)为沿t方向一簇不同t值下，θ与y的关系曲线。曲线从上到下，其斜率是逐渐变小的。对于图2，就物理原因而言是因为随着y的增加，岩石与裂隙间热量传递的距离越长，岩石内的过余温度变化越慢。

图2 θ与y的关系曲线Fig.2 Relationship betweenθand y

2.2 不同渗透流速下岩石内的过余温度

在工况b2=1.8×10-5m，Ts2=25℃，Tw=20℃下，不同裂隙水流速度所对应的岩石过余温度如图3(a)所示。由图3(a)可以看出，岩石的过余温度和影响范围随着时间的增长而逐渐变大，其趋势为在开始时随着y迅速变化，然后趋缓，最后趋于0，这与图2(a)所示互为验证。裂隙内水流渗透速度的变化，会影响温度场的分布。随着裂隙内水流渗透速度的加快，热交换的速度随之加快，缩短了到达热平衡的时间。渗透速度增大，导致热质迁移随之增大，在与岩石进行热交换达到平衡状态时，裂隙内部温度场的变化越剧烈。

2.3 不同隙宽下岩石内的过余温度

在工况Ts2=25℃，Tw=20℃，v2=0.000 4 m/s下，不同隙宽对应的岩石过余温度如图3(b)所示。由图3(b)可以看到，b越小，热质迁移的能力也越小，对岩石温度场的改变也越小。b的改变对岩石温度场的影响较小。

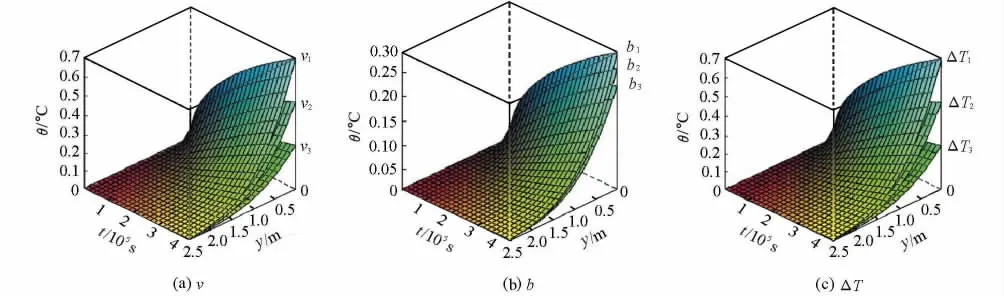
图3 不同v，b和ΔT下岩石内过余温度的变化Fig.3 Change of excess temperature of rock at different v，b，and ΔT

2.4 不同水流与岩石初始温度差下岩石内的过余温度

在工况v3=0.001 0 m/s，b=1.8×10-5m下，不同水流与岩石初始温度差所对应的岩石过余温度如图3(c)所示。岩石和裂隙水之间的相对温度越高，则其温度梯度的变化率越大，热量交换的速率也越快，岩石内温度场变化也越剧烈。

3 参数敏感性分析

由本文分析可知，参数v，ΔT和b对岩石的温度场都有影响，但其影响程度需进行敏感性分析。

3.1 分析方法

设一系统，其系统特性 P 主要由 n 个因素 α ={α1，α2，…，αn}决定，P=f(α1，α2，…，αn)。在某一基准α*={α，α，…}下，系统特性为P*［12］。分别令各因素在其可能的范围内变动，分析由于这些因素的变动系统特性，P偏离基准状态P*的趋势和程度，这种分析方法称为敏感性分析。

首先，需要进行无量纲化处理。为此定义无量纲形式的敏感度函数和敏感度因子，即将系统特性P的相对误差δp=/P与参数αk的相对误差δαk=/αk的比值定义为参数αk的敏感度函数Sk(αk):

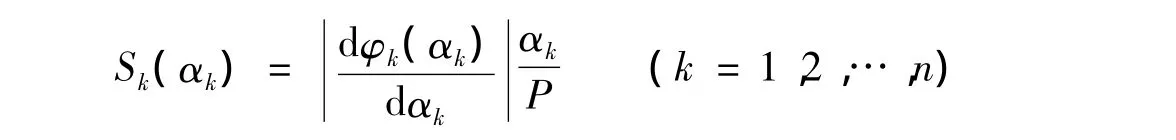
可绘出αk的敏感函数曲线Sk～αk。取αk=，即可得到参数αk的敏感度因子:

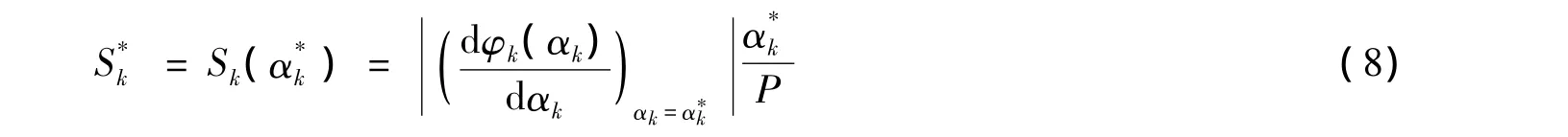
3.2 分析结果

系统特性即为裂隙岩石的过余温度θ，进行敏感性分析的参数为v，b，ΔT。根据传热模型，给出基准参数集:t*=120 h;y*=0.5 m;v*=0.0004 m/s;b*=1.8×10-5m;ΔT*=5℃。这里的基准参数集只是为了探讨参数的一般性规律，在实际工程及试验中可以有所不同。基准参数和本文传热模型的参数所选范围一致，v=0.00005 ～0.00100 m/s，b=5×10-6～5×10-5m，ΔT=5～15℃。分别逐次取定 v，b，ΔT 的值，计算出裂隙岩石的θ，用曲线拟合方法建立θ与v，θ与b及θ与ΔT的函数关系θ=φv，θ=φb和θ=φΔT，分别为

由式(8)，得敏感度函数 Sv，Sb和 SΔT分别为

相应的敏感度曲线见图4～6。

从图4～6可以看出，在给定的参数范围之内，参数v值较低时，对应的敏感度较高。随着v变大，敏感度逐渐降低，b的敏感度随v的增加而增加，参数ΔT的敏感度保持不变。将基准值v*=0.0004 m/s代入式(9)Sv，即得v的敏感度因子Sv*=1.098;同理得基准值下b和ΔT的敏感度因子 Sb*=0.216，SΔT*=1。

图4 Sv～v曲线Fig.4 Sv-v curve

由此，对于裂隙岩石的θ，即裂隙岩石的温度场而言，由分析结果可知v是最敏感参数，其敏感度高达1.098。也就是说，若v的计算值与实际值相差10%，则θ的相对误差δθ=10.98%。b敏感度较低，若误差为10%，引起θ的误差仅为2.16%。ΔT的敏感度为1，若误差为10%，引起θ的误差也为10%。因此，对于v和ΔT，计算值的选取应特别慎重。需要指出的是，该结论是针对特定基准参数集给出的，对于不同的基准参数集，也可得到相似的规律。

对敏感度因子进行排序，可以区分传热模型中的主要参数和次要参数，这样在工程应用或试验时就可以对方案进行优化。对本文的模型而言，在参数范围内由于b敏感度比较小，在测定其值时，不用要求过高的精度，从而节省费用。

图5 Sb～b曲线Fig.5 Sb-b curve

图6 SΔT～ ΔT 曲线Fig. SΔT-ΔT curve

4 结 语

通过建立岩石单裂隙传热数学模型，探讨了岩石单裂隙传热的一般规律，并对模型参数进行了敏感性分析，得到以下结论:(a)渗透作用下岩石温度场是裂隙水流速度、隙宽、水流与岩石初始温度差等综合作用的结果。(b)在给定参数范围内，岩石的温度场对参数v和ΔT的敏感性要比对b的敏感性高。

本文建立的岩石单裂隙传热数学模型具有理论清晰、计算过程简单明了等特点，可以用于分析单裂隙岩石渗流-传热的基本特征和参数敏感性，但也存在一些局限需要深入研究:裂隙岩石假设为隔水边界;边界条件考虑简单，与实际情况存在差距;没有考虑温度对渗流的影响;敏感性分析未考虑参数之间的相互影响等。

［1］项彦勇.裂隙岩体中非饱和渗流与运移的概念模型及数值模拟［J］.工程地质学报，2002，10(2):204-209.(XIANG Yanyong.Conceptual models and numerical modeling of unsaturated flow and transport in fractured rocks［J］.Journal of Engineering Geology，2002，10(2):204-209.(in Chinese))

［2］LAUWERIER H A.The transport of heat in an oil layer caused by the injection of hot fluid［J］.Appl Sci Res，1955，5:145-150.

［3］GRINGARTEN A C，WITHERSPOON P A，OHNISHI Y.Theory of heat extraction from fractured hot dry rock［J］.Journal of Geophysical Research，1975，80:1120-1124.

［4］SCHULZ R.Analytical model calculations for heat exchange in a confined aquifer［J］.Journal of Geophysics，1987，61:12-20.

［5］柴军瑞，仵彦卿.单裂隙非稳定流分析［J］.水利水运科学研究，2000(2):59-61.(CHAI Junrui，WU Yanqing.Analysis of unsteady flow through a single fissure［J］.Hydro-Science and Engineering，2000(2):59-61.(in Chinese))

［6］柴军瑞，韩群柱，仵彦卿.岩体一维渗流场与温度场耦合模型的解析演算［J］.地下水，1999，21(4):180-182.(CHAI Junrui，HAN Qunzhu，WU Yanqing.Checking computations on on-dimensional coupling model coupling temperature-seepage in rock mass［J］.Groundwater，1999，21(4):180-182.(in Chinese))

［7］张文捷，程荣兰，詹美礼，等.岩体渗流的一种改进数学模型［J］.河海大学学报:自然科学版，2010，38(1):52-57.(ZHANG Wenjie，CHENG Ronglan，ZHAN Meili，et al.Improved mathematical model for seepage in rock mass［J］.Journal of Hohai University:Natural Sciences，2010，38(1):52-57(in Chinese))

［8］孙粤琳，沈振中，张国双，等.瞬态温度场作用的岩体裂缝扩展追踪［J］.河海大学学报:自然科学版，2009，37(1):80-85.(SUN Yuelin，SHEN Zhenzhong，ZHANG Guoshuang，et al.Trace of crack propagation of rock under action of transient temperature field［J］.Journal of Hohai University:Natural Sciences，2009，37(1):80-85(in Chinese))

［9］于帆，张欣欣，何小瓦.非稳态平面热源法同时测量材料的导热系数和热扩散率［J］.宇航计测技术，2006，26(6):13-21.(YU Fan，ZHANGXinxin，HEXiaowa.Measurement of thermal conductivity and thermal diffusivity for materials on transient hotplane method［J］.Journal of Astronautic Metrology and Measurement，2006，26(6):13-21.(in Chinese))

［10］赵坚.岩石裂隙中的水流-岩石热传导［J］.岩石力学与工程学报，1999，18(2):119-123.(ZHAO Jian.Experimental study on flow-rock heat transfer in rock fractures［J］.Chinese Journal of Rock Mechanics and Engineering，1999，18(2):119-123.(in Chinese))

［11］林睦曾.岩石热物理学及其工程应用［M］.重庆:重庆大学出版社，1991.

［12］章光，朱维申.参数敏感性分析与试验方案优化［J］.岩土力学，1993，14(1):51-58.(ZHANG Guang，ZHU Weishen.Parameter sensitivity analysis and optimizing for test programs［J］.Rock and Soil Mechanics，1993，14(1):51-58.(in Chinese))