以HMX为基混合炸药撞击感度的计算方法
2013-10-11黄琛鸿刘玉存袁俊明
黄琛鸿,刘玉存,袁俊明
(中北大学化工与环境学院,山西 太原,030051)
撞击感度是指在机械撞击作用下,炸药发生燃烧或爆炸的难易程度。它以在一定条件的落锤实验中炸药样品的爆炸概率或50%爆炸概率下的特性落高H50表征[1]。而此类实验存在一些不足与局限:(1)实验具有一定的危险性;(2)实验受外界条件影响较大,再现性差;(3)对于设计阶段的化合物,无法通过实验来获知其撞击感度[2]。因此,单纯应用实验来确定炸药的撞击感度是不能满足需要的,有必要运用理论方法对炸药的撞击感度进行估算与预测,以弥补实验研究的不足。
近年来,很多学者在预测单质炸药撞击感度方面做了很多努力,包括采用炸药的分子结构参数,人工神经网络、定量结构-性质关系(QSPR)模型[3-5]等。但是对于混合炸药撞击感度的预测,所做的工作还不多。A.V.Dubovik[6]提出一个近似计算混合炸药发生爆炸时的临界压力(pcr)和临界厚度(hcr)的物理模型。临界压力(pcr)和临界厚度(hcr)从理论上精细地(hcr值可准确到±0.01 mm)表达了炸药的撞击感度的特性,但由于H50的测定更容易操作,所以更适合于常规测试。为了充分挖掘炸药撞击感度与分子结构的关系,本文基于单质炸药活性指数与撞击感度的关系,对混合炸药活性指数与撞击感度关系进行了研究,从而达到预测混合炸药撞击感度性能的目的。
1 单质炸药活性指数与撞击感度的关系
炸药分子结构活性的外在表现为:炸药撞击感度的大小可以是结构不稳定性的一种标志。炸药分子活性的大小受到其含有的活性基团的性质、数量以及各个活性基团间相互作用的影响。邢郁明教授认为在炸药中各种基团对活性指数的贡献值具有加和性,各基团活性指数的贡献值加和所得总活性指数贡献值为炸药的摩尔活性指数[7]:

式(1)中:M为炸药的摩尔质量,Ki、Ni分别为第i种基团或原子对指数的贡献值和分子中基团或原子的数目。F值大表示分子结构的活性大,易被激发而感度高,反之则感度低。应用式(1)计算了35种单质炸药的摩尔活性指数(见表1),特性落高H50(35组数据撞击感度试验条件:12型工具,5kg落锤)从相关数据手册[8-9]查得。
对F与H50作图,如图1所示。从图1中可以看出单质炸药F与H50具有较好的递变关系,分子的活性指数F越大,撞击感度H50值就越小,炸药的感度就越大;反之,F的值越小,撞击感度H50值就越大,炸药就越钝感。

图1 单质炸药活性指数F与H50关系图Fig.1 Relationship between F and H50 for the single explosive
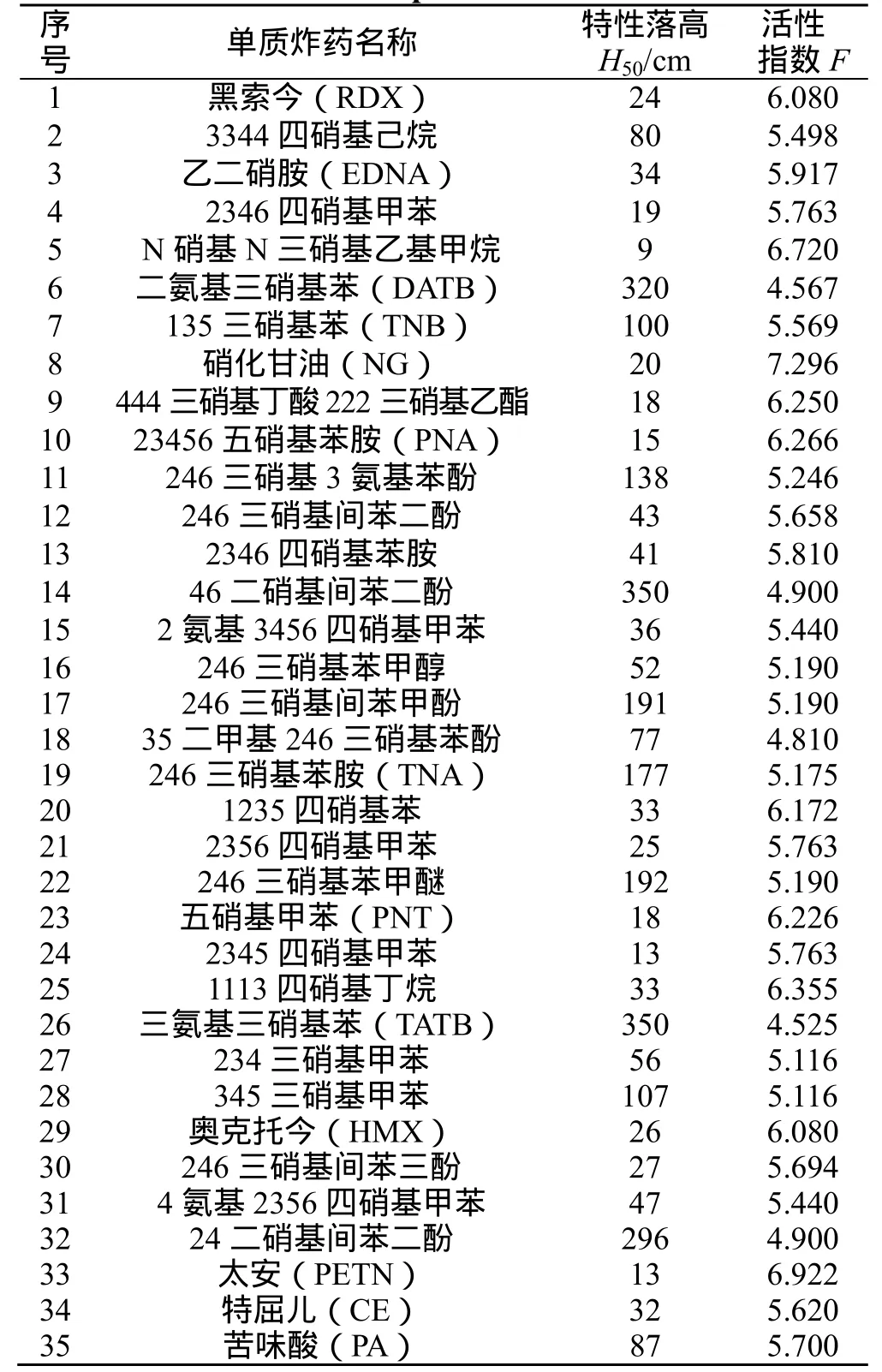
表1 所选35种炸药的相关参数Tab.1 The correlative parameters of 35 kinds of selected explosives
2 混合炸药活性指数与撞击感度的关系
2.1 附加物分类及附加物活性指数的赋值
在混合炸药中除了主体炸药外,还有含量不等的附加物,由于附加物也影响到混合炸药的撞击感度,于是对附加物的活性进行赋值,对于分子结构较简单的附加物,应用式(1)通过计算求得;对于结构复杂的一些高分子附加物和无机物,根据其在不同的混合炸药中含量的不同,通过解方程计算求得;对于个别的附加物,由于数据过少,无法通过上面两种方法求得,则根据其在炸药中表现的活性大小[10]并与单质炸药HMX(F值为6.08)的活性做对比,综合确定其活性指数。
2.2 混合炸药活性指数与特性落高对数的关系
以单质炸药的活性指数与特性落高的关系为基础,为了减少变量对结果的干扰,选取了以HMX为基的混合炸药进行探讨,混合炸药的摩尔活性指数即为单质炸药的活性指数和附加物的活性指数按照质量比进行加和:

式(2)中:Wi、Fi分别为第i种炸药的质量分数和活性指数,Wj、Fj分别为第j种附加物的质量分数和活性指数。将表1和表2中的数值代入到式(2)中,得出混合炸药摩尔活性指数F混,特性落高H50及其对数值一并列于表3。

表2 附加物活性指数赋值Tab.2 Activity index of appendage
利用SPSS软件对混合炸药的活性指数F混与其特性落高的对数lgH50进行回归分析,得出活性指数与特性落高的经验模型,如图2所示。
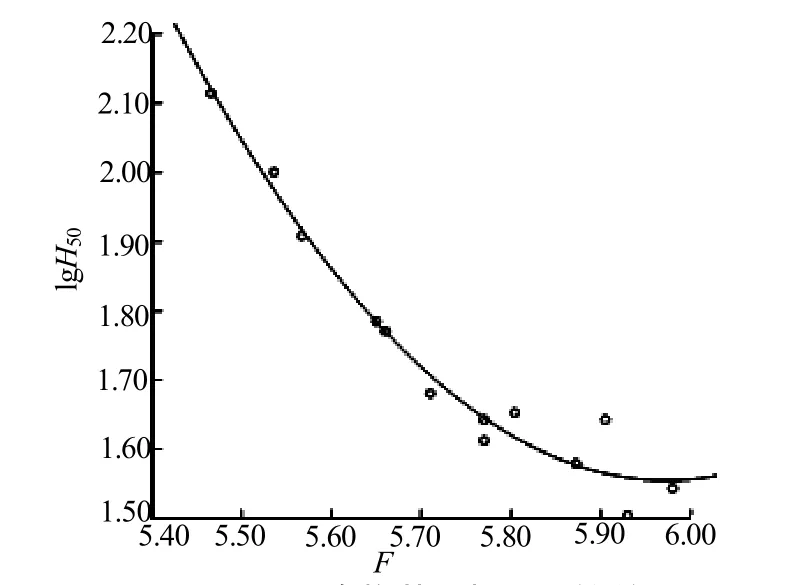
图2 混合炸药F混与lgH50的关系Fig.2 Relationship between F混 and lgH50 for the composite explosives
图2的经验模型为:

式(3)中:H50为混合炸药的特性落高;F混为混合炸药总的活性指数。其中,曲线拟合优度R2=0.968,显著性检验统计量为151。
2.3 经验模型结果验证
通过式(3),求得相关文献中混合炸药特性落高的预测值,与其实际值列于表4。将混合炸药特性落高的预测值与文献值做对比,如图3所示。
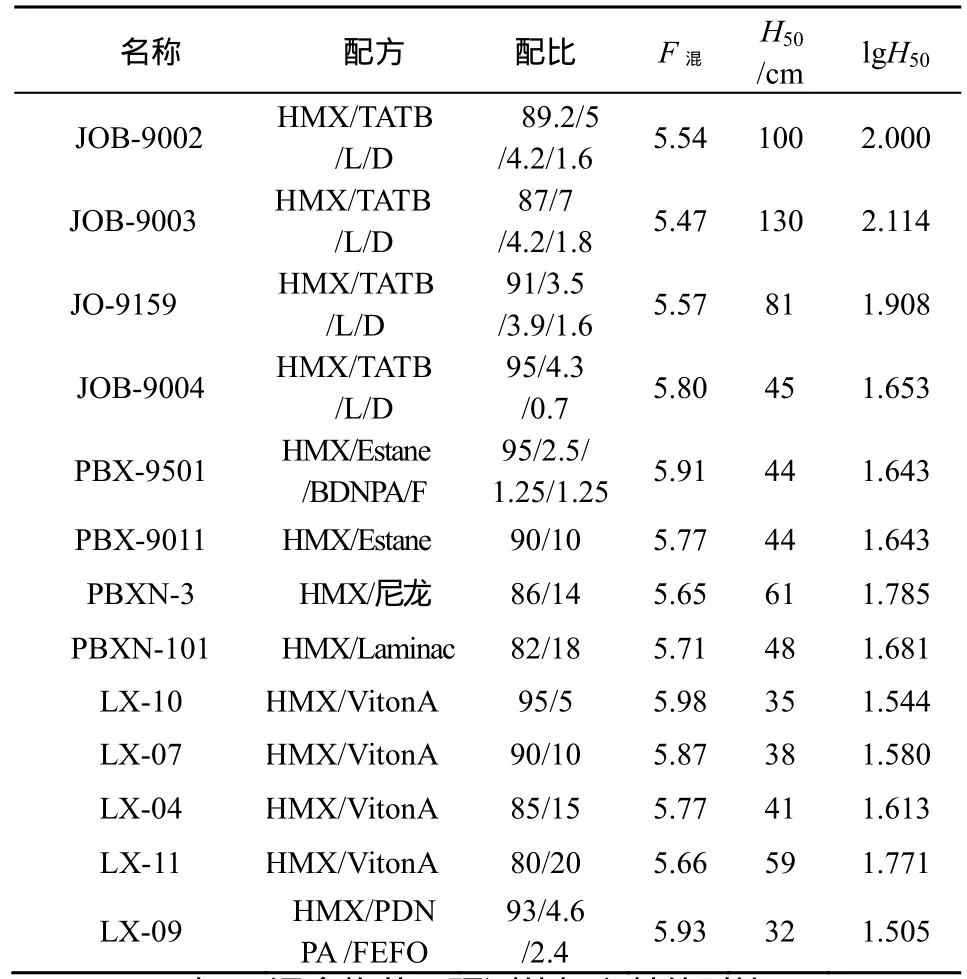
表3 混合炸药活性指数及其lgH50Tab.3 Activity index and lgH50 of composite explosives

表4 混合炸药H50预测值与文献值对比Tab.4 Comparison of predictive value with literature value of H50 of composite explosives
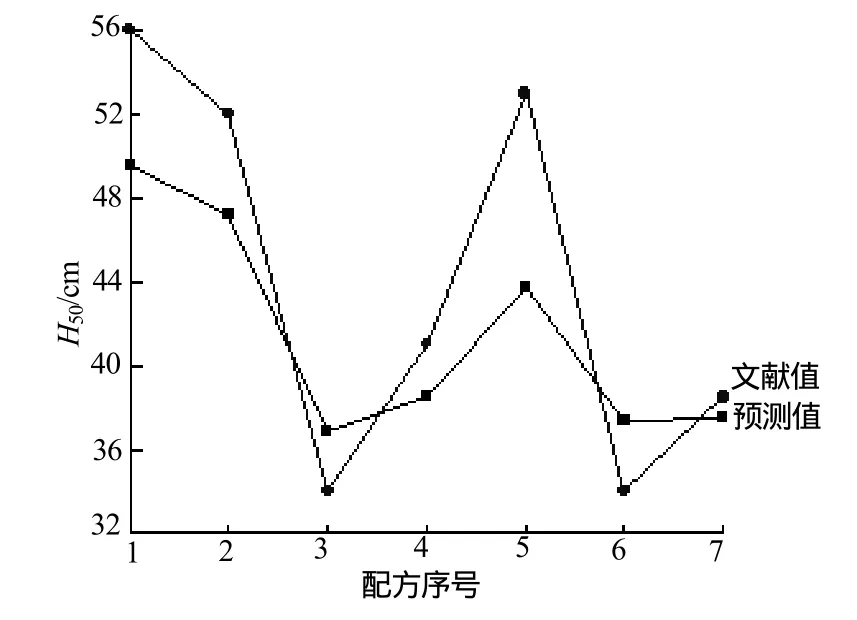
图3 H50预测值与文献值比较Fig.3 Comparison of predictive values with literature values of H50
从图3可以看出回归方程是显著的,具有较好的拟合效果,可以从趋势上对混合炸药撞击感度做出预测。其中,有一个数据的偏差较大,一方面的原因是该混合炸药中附加物的含量较少,导致附加物的影响被放大,另一个原因可能是由于选择的实验数据不是很多,导致附加物的活性指数赋值具有一定的偏差。
3 结论
(1)单质炸药的撞击感度H50与活性指数F有较一致的递变趋势, 即随着F的增加而减小。以该关系为基础,将活性指数的概念推广至混合炸药。
(2)运用炸药感度理论分析和统计软件 SPSS拟合数据相结合的方法,建立了一个以HMX为基的混合炸药撞击感度的经验模型。该模型不同于其它预测方法有着繁杂的计算过程,较容易计算,能为研究者提供一个更简单的预测混合炸药撞击感度的途径,且有望将相对误差控制在10%以内,甚至更小。
(3)为了减少变量,本次经验模型仅研究了奥克托今为基的混合炸药,而对于其他混合炸药,还有待于进一步的研究。
[1]金韶华, 王伟, 松全才. 含能材料机械撞击感度判据的认识和发展[J]. 爆破器材, 2006, 35(6): 11-14.
[2]王睿, 蒋军成, 潘勇. 硝基含能材料预测研究进展[J]. 工业安全与环保,2010,36(7): 19-22.
[3]Mohammad Hossein Keshavarz. Prediction of impact sensitivity of nitroaliphatic, nitroaliphatic containing other functional groups and nitrate explosives[J]. Journal of Hazardous Materials, 2007, 148(3): 648-652.
[4]Mohammad H K, Mohammad J. Investigation of the various structure parameters for predicting impact sensitivity of energetic molecule via artificial neural network[J]. Propellants,Explosives, Pyrotechnics, 2006, 31(3): 216-225.
[5]杜军良,舒远杰.硝基炸药撞击感度的QSPR研究[J]. 绵阳师范学院学报,2009,28(11): 45-49.
[6]A.V.Dubovik.Approximate method for calculating the impact sensitivity indices of solid explosive mixtures[J].Combustion,Explosion and Shock Waves, 2001,37(1): 99-105.
[7]周霖. 爆炸化学基础[M]. 北京:北京理工大学出版社, 2005.
[8]董海山, 周芬芬. 高能炸药及其相关物性能[M]. 北京:科学出版社, 1989.
[9]钟一鹏, 胡雅达,江宏志. 国外炸药性能手册[M]. 北京:兵器工业出版社, 1990.
[10]孙国祥. 高分子混合炸药[M]. 北京:国防工业出版社, 1985.
[11]B. M. Dobratz. Properties of chemical explosives and explosive simulation[R]. Lawrence Livermore National Laboratory, 1974.
[12]胡荣祖, 赵凤起. 高聚物黏结炸药JH-94和JO-96撞击感度特性落高的估算[J]. 含能材料, 2009,17(3): 251-254.
[13]刘树浩, 张景林. HMX的氟橡胶包覆技术及其撞击感度研究[J]. 中国安全生产科学技术, 2011,7(6): 5-8.
