飞机结构中凹陷应力集中系数初步确定

汤庆辉，柯曾言

（中航工业洪都，江西南昌330024）

0 引言

在飞机的生产和使用过程中，结构可能会因为人为和非人为因素出现某些缺陷。这些缺陷主要包括凹陷、划痕、腐蚀和雷击烧伤及多余孔等等。对于这些缺陷，如果没有进行有效的修理和监控，对飞机的飞行会带来较大的安全隐患。纵观国外，这些缺陷的疲劳和裂纹扩展分析都得到了较好的论证。而在国内，仅仅对其静强度进行了分析，而疲劳和裂纹扩展分析还没有过多的涉及。所以很有必要对这些缺陷进行疲劳和裂纹扩展分析。本文详尽介绍了凹陷的应力集中系数的初步确定，为凹陷的疲劳分析提供必要的条件，进而确定凹陷是否满足疲劳寿命要求。

1 凹陷的形式和种类

图1 凹陷的结构形式

凹陷是由于重物坠落或与其他物体碰撞产生的，一般可假定其为球冠，用直径和深度来表示凹陷的形式，如图1所示，W为凹陷外形大小，D为凹陷深度，t为板的厚度。根据凹陷发生的部位可以定义凹陷的种类。

1）如果凹陷发生在外部蒙皮上，并且蒙皮内部没有与任何结构相连，可以称此种凹陷为柔性凹陷。

2）如果凹陷发生在外部蒙皮上，并且蒙皮内部与长桁相连(并且认为凹陷不允许发生在与梁或框连接处)，可以称此种凹陷为硬性凹陷。

2 凹陷的应力集中系数的初步确定

凹陷的疲劳分析可以采用名义应力法，名义应力法是根据危险部位的名义应力（最大主应力）和应力集中系数Kt，对照Kt下材料的S-N曲线，应用线性累积损伤理论，估算出危险部位的裂纹形成寿命。名义应力法流程中主要的步骤是应力集中系数的确定，本文利用有限元方法对凹陷的应力集中系数进行初步确定。

2.1 凹陷应力集中系数计算的有限元模型建立

设定一块长300 mm，宽200 mm的板中央有一凹陷。分别对某个参数进行变化，而另外两个参数不变化来分析凹陷的应力集中系数，共有三组情况，对应于板的厚度、凹陷深度和宽度变化。在模型中一边施加固支约束，另一边均匀施加2000 N的受拉载荷，用于模拟最大主应力。有限元模型见图2。

图2 应力集中系数分析的有限元模型图

2.2 应力集中系数计算结果

各组有限元应力结果及根据结果计算出的应力集中系数见表1，各参数与应力集中系数的关系见图3至图5。

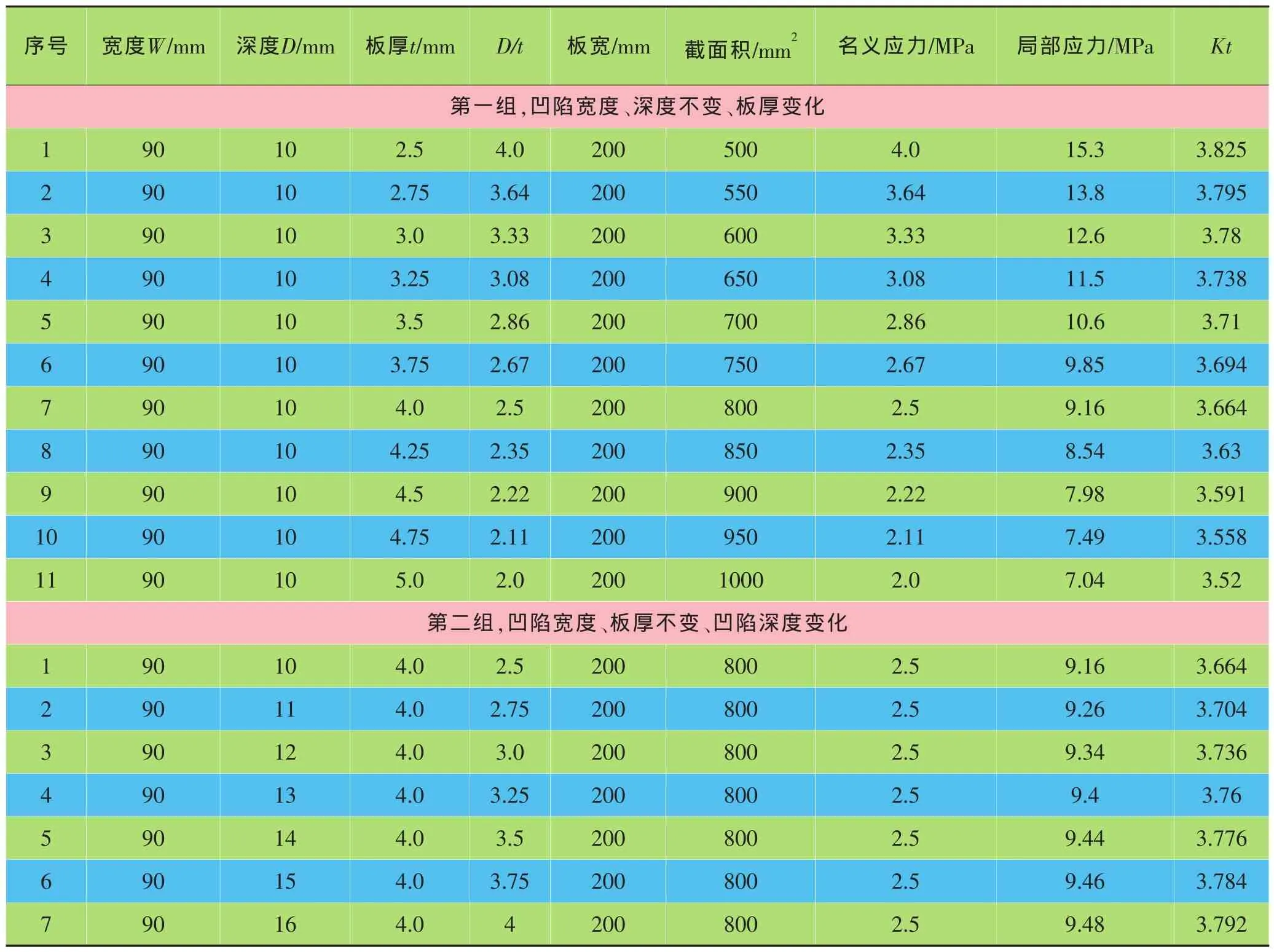
表1 各组情况凹陷的应力集中系数结果

续表1

图3 应力集中系数随板厚t的变化情况

2.3 应力集中系数结果分析

依据表1中数据和图3至图5，可以看出凹陷的应力集中系数随板厚的增大而减小、随凹陷深度的增大而增大、随凹陷宽度的增大而增大。

2.3.1 拟合曲线的确定

依据图3至图5，根据经验及工程判断可以获得Kt与各参数之间的趋势如下：

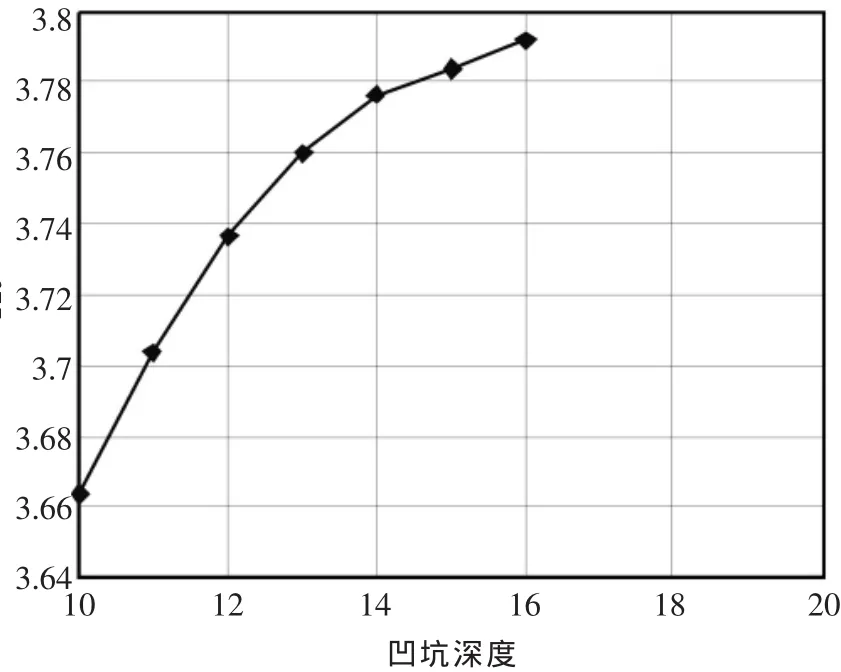
图4 应力集中系数随凹陷深度D的变化情况

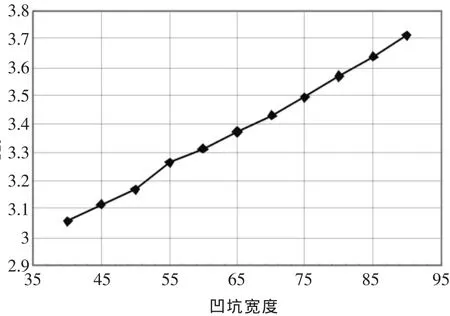
图5 应力集中系数随凹陷宽度W的变化情况

1） 根据图3（b）能够得出Kt与板厚的倒数（1/t）有对数关系；

2）根据图4能够得出Kt与凹陷深度（D）有对数关系；

3）根据图5能够得出Kt与凹陷宽度 （W）有线性关系。

按以上Kt与凹陷参数的趋势关系，可以初步确定出应力集中系数与凹陷参数之间的表达式：， 公 式 中 a0、a1、a2为常量。

2.3.2 最小二乘法确定a0、a1、a2常量对于应力集中系数与凹陷参数之间的公式，设定W为x，为y，Kt为f(x，y)。 则Kt用公式表示为：f(x,y)=a0+a1·x+a2·y，公式是二元多项式，可以利用曲线拟合的二元最小二乘法确定系数a0、a1、a2。对于二元最小二乘法就是根据离散点集{(xi，yi，zi)，i=1，m}与要拟合出的函数f(xi,，yi)的误差平方和I(a0，a1，a2)最小而确定拟合函数f(x，y)。误差平方和：

化成矩阵：

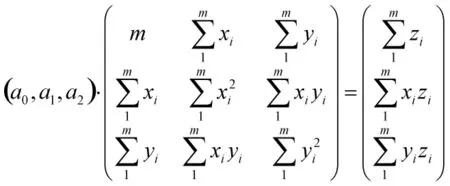
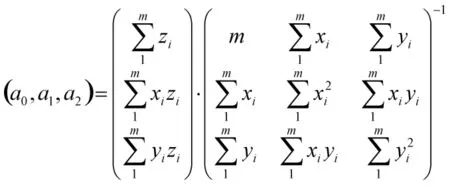
利用表1中的数据和以上公式可计算出(a0,a1,a2)=(2.12403,0.01295,0.90101)，因此凹陷的应力集中系数可表达为：

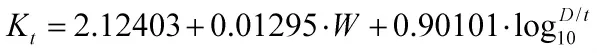
2.3.3 拟合公式的检验与误差分析

Kt的回归平方和残差平方和分别定义如下：

离差平方和：

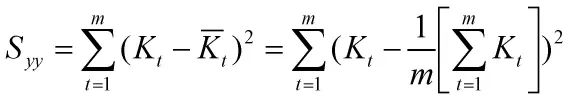
离差平方和Syy为残差平方和U和回归平方和V之和：Syy=U+V

这时V的计算公式为 V=Syy–U

根据线性回归理论知V愈大（或U愈小）则表示Kt与这些自变量的线性关系愈密切，回归的规律愈强，回归出的结果可信度愈高。

为了表征这一特点，定义复相关系数R为

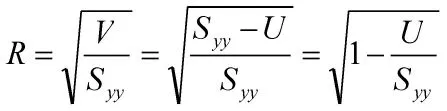
显然，R越接近于1，表明y与x1，x2，…，xn的线性关系越密切，也就是说回归出的回归方程的系数矩阵有较好的精度。

本文经计算得出U=0.00756，Syy=1.33741，V=Syy-U=1.32985

R的值较接近于1，系数矩阵(a0，a1，a2)精度较好。

除了用R进行线性检验外，还要利用F值对整个回归方程进行显著性检验。F值如下定义：

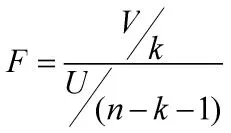
式中给出的F也服从自由度为k，n-k-1的F分布，如令α=0.05，将由计算出的F值与相应的临界值作比较，如F大于临界值，则表明所建立方程是良好的。本文的自由度为2，共有29组数据，

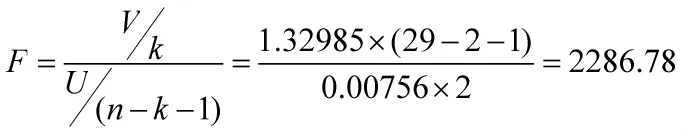
F0.05(2,26)=3.37，由于F≫F0.05(2,26)，故认为线性回归得出的凹陷的应力集中系数方程式是显著的。

3 结论

本文根据有限元分析方法初步确定的凹陷应力集中系数公式，在经过R和F检验后，公式的精度较好，同时，对于凹陷来说，有限元分析难于考虑一些工艺参数和其他因素的影响，在经过试验验证对本文的公式进行修正后，可用于实际工程的应用，从而为凹陷的疲劳寿命分析提供必要的依据。

[1]李庆扬，王能超，易大义.数值分析第5版.北京：清华大学出版社，2011.

[2]数理统计编写组编.数理统计.西安：西北工业大学出版社，1999.