数字滤波语音信号除噪设计
2013-10-10窦海鹏
窦海鹏
(山西大学商务学院 信息学院,山西 太原 030031)
0 引 言
语音是人类传递信息的重要手段,但是在现代的各种通信系统中,人们在获取语音的同时,总是会受到外界环境的干扰和影响,各种自然噪声和人为噪声会掺杂在语音信号中,严重影响语音质量。因此,利用数字信号处理技术对语音信号进行处理,滤除掺杂在其中的非必要噪声是很必要的,也是具有实际意义的研究课题。
首先提取一段语音信号,并在其中掺杂高频噪音。然后利用Matlab仿真软件设计一个FIR数字滤波器[1-6],将掺杂在语音信号中的高频噪音消除,并分析比较消除高频噪音前后语音信号的时域和频域特性[7-9]。仿真结果表明,通过窗函数法设计的FIR数字滤波器可以有效地抑制带外噪声,提高话音质量,对实现语音信号的处理具有一定的实用价值。
1 原始信号的采集与处理
1.1 原始信号的采集及时域分析
为了研究语音除噪技术,首先应采集一段语音信号。使用电脑声卡录制一段语音信号,利用Matlab中的wavread命令读入该语音信号,将它赋值给某一向量。另外,可以通过sound命令回放该语音,感受声音的变化。语音采集程序如下:

通过合理选择采样位数可以衡量声音波动变化情况,而采样频率表示的是录音设备在1s内对语音信号的采样次数,所以,采样频率越高,对声音的还原就越有利。
电脑采集的原始语音信号的时域波形如图1所示。

图1 原始语音信号时域波形
由图中可以看出,语音信号随时间的延续而缓慢变化,是一种非平稳的时变信号。语音信号携带了需要传递的信息,根据人类发声时音调和音色的不同,提取的语音信号采样值的幅度和时间变化也各不相同。
1.2 信号加噪及频谱分析
处理语音信号的目的是为了更有效地提取信号中所携带的信息,所以在研究语音信号时域特性的同时,有必要研究其频域特性。而离散傅里叶变换是信号处理中的一个重要变换工具,可以将一个信号序列从时域表示转换到频率域表示,在信号处理中有广泛的应用。Matlab数字信号处理工具箱中的函数FFT是对离散傅里叶变换进行快速计算的有效算法,可以直接调用,调用格式如下:

其中,N是信号截取的长度。
利用FFT对采集的语音信号进行处理的频谱如图2所示。

图2 原始语音信号频谱
从图中可以看出,人类的语音频率范围主要集中在4 000Hz以内,属于低频信号。若此时在4 000Hz之外的较高频率处掺杂了干扰,将会对语音的质量造成影响。为了比较加入干扰前后的语音质量,现利用Matlab产生一个10.8kHz的余弦信号作为噪声加入到语音信号中,并对其进行频谱分析。其主要程序如下:

加入噪声后的信号时域波形及加入噪声前后的信号频谱比较如图3所示。
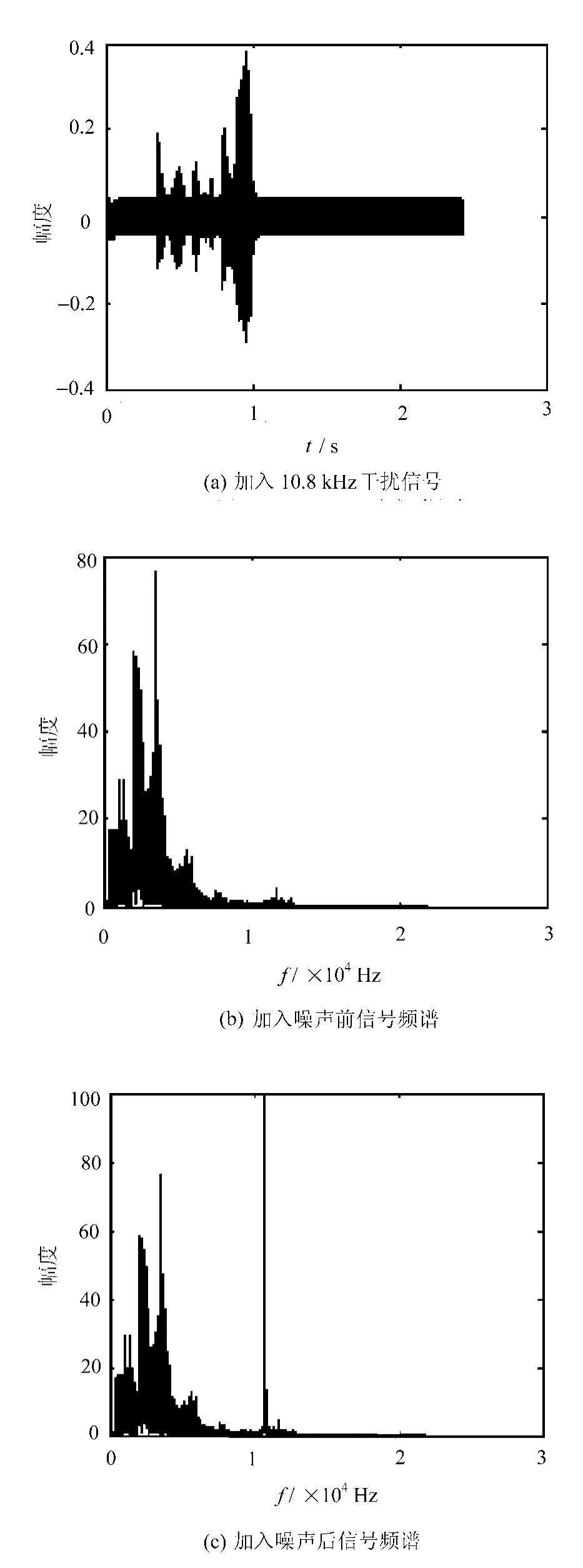
图3 加入噪声后的信号时域波形及频谱比较图
从时域图中可以看出,(a)加入10.8kHz的干扰信号后,在整个语音信号存在的时间过程中多出了高频成分。通过对加入噪声前信号频谱(b)和加入噪声后信号频谱(c)的比较发现,加入噪声后,在原语音信号频谱图的10.8kHz频率附近多出一个高频脉冲。若通过sound命令回放该语音,可以听到一个刺耳的噪音,而语音信号本身变模糊,话音质量变差。
2 数字滤波器的设计
数字滤波器在数字信号处理的各种实际应用中发挥着巨大的作用,它通过对采样的数据信号进行数学运算来达到频域滤波的目的,文中采用基于窗函数设计法的有限脉冲响应数字滤波器(FIR)滤除高频噪音。FIR数字滤波器在保证幅度特性满足技术要求的同时,又具有严格的线性相位特性,稳定和线性相位是其最突出的优点。因此,FIR滤波器在图像处理、通信等领域都有广泛的应用。
设计FIR数字滤波器就是要找到一个系统函数 H(z),使其频率响应函数 H(ejω)逼近滤波器要求的理想频率响应函数Hd(ejω)。
设线性相位理想低通滤波器的频率响应为:

其对应的单位脉冲响应hd(n)为:

由上式看出,hd(n)是无限长的,且是非因果序列,为构造一个长度为N的线性相位FIR数字滤波器,需将hd(n)截取一段,设截取的一段用h(n)表示,即

式中:h(n)——需要设计的滤波器单位脉冲响应。
从上述分析看出,利用窗函数法设计FIR滤波器的关键问题是选择合适的窗函数ω(n),在选择窗函数时,应考虑到被处理信号的性质及处理要求等。文中根据需滤除的高频信号的频段范围、强度和衰减等要求,选用旁瓣幅度较小的汉宁窗。
Matlab信号处理工具箱提供了丰富、简便的设计实现FIR滤波器的方法,使繁琐的程序设计简化成函数的调用,根据文中对语音信号除噪的要求,选用汉宁窗,确定所设计的FIR低通滤波器的设计指标为:Wp=0.15*pi,Ws=0.25*pi,设计程序如下:


设计的FIR低通滤波器的幅频特性如图4所示。
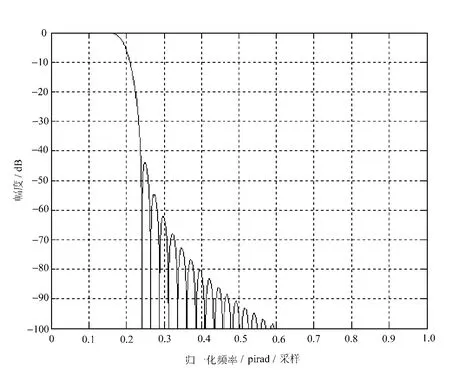
图4 FIR低通滤波器的幅频特性
从图中可以看出,选择汉宁窗使滤波器的主瓣包含了更多的能量,相应旁瓣幅度很小,达到-40dB以下,满足滤波要求。
3 利用数字滤波器消除语音信号的噪声
利用文中设计的FIR数字滤波器对掺杂了高频噪音的语音信号进行滤波处理,程序如下:


滤波前后语音信号的时域波形图及频谱比较结果如图5所示。
由图中可见,该低通滤波器滤除了4 000Hz以上的高频信号(包括掺杂的余弦干扰),保留了4 000Hz以内的低频语音信号,符合低频语音信号的特性。回放声音发现,语音信号中夹杂的高频刺耳的蜂鸣声消失了,声音变得比原始语音低沉平滑,这是因为利用汉宁窗设计的FIR滤波器不仅滤掉了高频噪声,而且把原始信号中很小的一部分高频分量也滤掉了,仅余下了较低频率的语音信号,说明达到滤除高频噪音信号的目的。
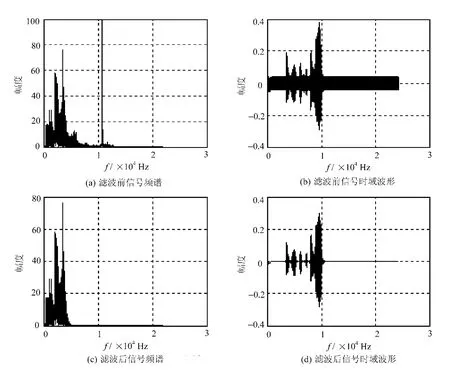
图5 滤波前后语音信号的时域波形图及频谱比较
4 结 语
利用Matlab仿真软件设计的FIR数字滤波器,可以很好地将掺杂在语音信号中的高频噪音消除,提高话音质量。通过分析比较消除高频噪音前后语音信号的时域和频域特性发现,通过窗函数法设计的数字滤波器方法简单,准确可靠,是数字信号处理中常用的技术之一,对实现语音信号的处理具有一定的实用价值。
[1]丁爱华,黄朝耿,李刚.一种新型低复杂度的IIR格型滤波器[J].电子学报,2013(9):1703-1708.
[2]陶炳坤,陈鹏宇,李楠.FIR数字滤波器的Matlab仿真和DSP的实现[J].电子设计工程,2013,21(9):177-179.
[3]王晓燕,李杰,董玉才.基于FIR数字滤波器随机振动信号频时域转换方法[J].北京理工大学学报,2012,32(7):685-688.
[4]柴西林,邵照勇.基于 MatlabGUI的数字滤波器设计及其应用[J].微型机与应用,2005,31(14):3-6.
[5]王淑娇.数字滤波器的设计与参数选择[J].科技资讯,2011(35):32.
[6]李锶,安伟科.一种FIR高阶多通带数字滤波器的优化设计方法[J].电力自动化设备,2007,27(8):66-68.
[7]付大丽,党幼云.数字滤波器在语音信号处理中的应用[J].电声技术,2012,36(8):62-65.
[8]冯彦君,靳鸿,章晓眉.应用 Matlab分析语音信号[J].光电技术应用,2011,26(3):57-60.
[9]周玲.基于Matlab的语音信号数字滤波处理[J].安庆师范学院学报,2011,17(3):46-49.
