一种基于谱峭度的局部放电信号提取新方法

陈 刚，刘志刚，张巧革

（西南交通大学 电气工程学院，四川 成都 610031）

0 引言

随着电力系统的不断发展，电压等级越来越高，对大型电力设备的绝缘性能要求也越来越高。局部放电会逐渐腐蚀、损坏绝缘材料，使放电区域不断扩大，最终导致整个绝缘体击穿。电力设备内部早期故障产生的局部放电信号很微弱，而且现场存在着强烈的电磁干扰，局部放电信号往往被淹没在噪声中，对局部放电信号的检测和提取产生直接影响。因此，研究强噪声背景下的局部放电信号提取，对大型电力设备早期绝缘故障诊断有很重要的意义[1-3]。

局部放电的干扰信号按照其波形可分为窄带周期型干扰、平稳随机型干扰和随机脉冲干扰[4]。电力系统的载波通信、高频保护信号和无线电广播对监测的干扰属于窄带周期型干扰；各种设备以及监测线路中的白噪声属于平稳随机型干扰；输电线路和邻近电力设备的电晕放电和内部放电干扰信号属于脉冲型干扰。本文主要讨论平稳随机型干扰和窄带周期型干扰在局部放电信号提取中的影响。

目前研究局部放电信号提取的方法有小波阈值去噪法[5-7]、HHT 方法[8-10]等，它们对局部放电信号的处理都能达到一定的效果，但是也都存在各自的问题。如小波的多分辨率特性能将信号在不同尺度下进行多分辨分解，但是小波变换的基函数的选取和最佳小波分层数的确定都存在问题，所以不能保证最优的分解效果。HHT方法可以分析非线性、非平稳的信号，具有良好的局部适应性，但这种方法会产生虚假分量，存在端点效应和模态混叠，且各分量的物理意义不是很明确。

本文提出将谱峭度 SK（Spectral Kurtosis）[11-12]的方法应用到局部放电信号的提取中。谱峭度属于高阶统计量的范畴，是一个4阶累积量，理论上能够完全抑制高斯噪声，表征信号中的非平稳和非高斯信号，并且能够确定其在频带上的位置。谱峭度方法凭借其良好的统计特性已经在机械振动系统的故障诊断，如齿轮故障诊断[13]、轴承早期故障诊断[14-15]中得到广泛应用，并取得了很好的成果。本文通过求取谱峭度，根据其设计自适应最优带通滤波器，对局部放电信号进行滤波，从强噪声中提取出局部放电信号，并进行2～3层小波平滑去噪，以进一步提高局部放电信号特征的提取精度。通过仿真实验分析验证了本文方法的可行性和有效性。

1 谱峭度

1.1 谱峭度的定义

峭度是随机变量的4阶累计量，作为一个全局性指标不能反映特定信号分量的变化情况，因此，不适合强噪声环境下的状态检测问题。为了克服峭度在工程应用中的不足之处，Dwyer提出了谱峭度方法[16]。

考虑非平稳信号的Wold-Cramer分解，定义Y（t）为由信号 X（t）激励的系统响应，则 Y（t）可以表示为[17]：

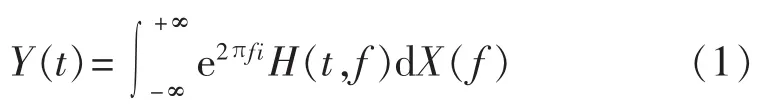
其中，H（t，f）是系统的时变传递函数，可解释为信号Y（t）在频率 f处的复包络。 在实际系统中，H（t，f）是随机的，可表示为 H（t，f，w），w 表示滤波器时变性的随机变量。

S2nY（t，f）为 2n 阶瞬时矩，是复包络能量的度量，定义为：

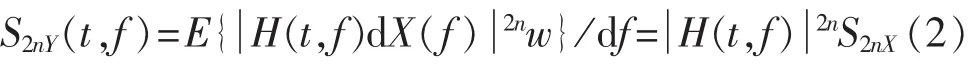
因此，当n分别取1、2时，谱峭度可定义为：

1.2 谱峭度的性质

谱峭度有很多性质[17]，本文主要给出以下2个性质。

性质1一个纯的平稳过程Y（t）的谱峭度为：

特别地，一个纯的平稳高斯过程Y（t）的谱峭度为0。

性质2 一个条件非平稳随机过程Z（t）=Y（t）＋N（t），N（t）是添加的噪声信号，它与 Y（t）相互独立。N（t）的谱峭度为：

其中，ρ（f）=S2N（f）／S2Y（f），为噪信比。 根据式（5）可以得出，ρ（f）越大，谱峭度值越接近于 0，而 ρ（f）越小，谱峭度值近似等于KY（f），因此在整个频域进行搜索，可以找到谱峭度最大的频带。

2 基于谱峭度的局部放电去噪算法

本文根据局部放电信号的特征，提出一种基于谱峭度的局部放电信号提取新算法。该算法核心思想是首先求取出含噪局部放电信号的谱峭度，然后根据谱峭度设计自适应带通Wiener滤波器，再进行小波平滑去噪，提取出局部放电信号。

2.1 估计谱峭度

根据谱峭度的定义，本文采用短时傅里叶变换（STFT）的方法实现峭度谱的估计[18]，如式（6）所示。

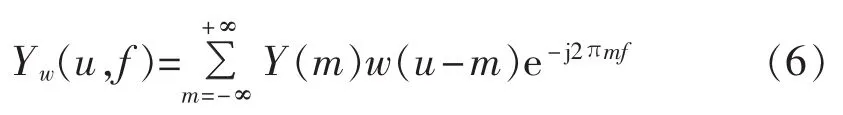
其中，Y（m）为一个随机过程；w（m）为窗函数，其长度为 Nw。

定义 Yw（u，f）的 2n 阶谱矩为：

其中，〈·〉l表示l阶时平均。因此，当n分别取1和2时，基于STFT的谱峭度的估计值为：

2.2 自适应最优带通滤波器设计

Wiener滤波器设计简单，性能优越，但是其参数是固定的。要设计这种滤波器，必须对信号和噪声的统计特性有先验知识，但是在实际中，常常无法预先知道这些统计特性，或者它们是随时间变化的，从而用Wiener滤波方法不能实现最优滤波。Wiener滤波器可表示为[18]：

根据1.2节中的谱峭度性质2，Wiener滤波器可以通过求取相应信号的谱峭度来实现，即：

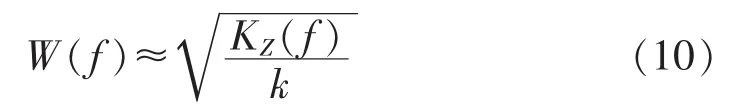
其中，k为未知参数，其获取可以先假设一个比较小的值代入式（10），构造Wiener滤波器，再通过多次迭代，找到使滤波器滤波后相应输出信号的峭度值（可用MATLAB自带的峭度程序求取）的最大值，从而确定参数 k[18]。

局部放电信号的窄带周期干扰可用一系列频率不同的正弦信号表示，平稳随机干扰可看作是白噪声。根据1.2节中的谱峭度性质1，理论上窄带周期干扰的谱峭度恒为-1，平稳随机干扰的谱峭度为0。但是基于STFT方法估计出的谱峭度值不是理论上的-1或者0，而是在它们附近波动。只根据式（10）设计出来的滤波器会包含其他频带的噪声，因此本文设置阈值σ来限定谱峭度的值。根据实际应用，σ可设置为：

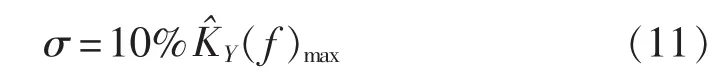
其中，KˆY（f）max为信号谱峭度的最大值。 谱峭度小于阈值σ可以认为是窄带周期干扰和白噪声信号，在设计滤波器时将其直接滤除。根据该方法设计出的滤波器是一个完全由数据驱动的自适应滤波器，不必知道信号的先验知识就能进行最优滤波。

2.3 小波平滑去噪

经过滤波过后的信号仍然存在与局部放电频率相同或相近的噪声信号，只需进一步通过2～3层的小波阈值平滑去噪，便可以得到更为精确的局部放电特征信号。

本文选用与局部放电信号波形匹配较好的db8小波进行分解[20]，对经过自适应最优Wiener带通滤波器处理后的局放信号进行2～3层小波分解，采用无偏似然估计软阈值方法就可将局部放电信号提取出来。

综上所述，本文提出的基于谱峭度的局部放电信号提取算法的主要步骤如图1所示。

3 仿真验证

实际电力设备运行中，采集到的局部放电信号经常表现为指数衰减振荡形式，因此在理论分析中，通常可以采用以下2种数学模型来表示局部放电信号的形式[19]。

图1 算法原理Fig.1 Principle of algorithm

单指数衰减振荡型（图 2（a））：

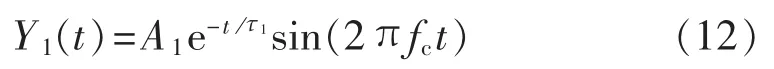
双指数衰减振荡型（图 2（b））：

其中，A1、A2为信号幅值；τ1、τ2、τ3为衰减系数；fc为振荡频率。

图2 2种局部放电信号Fig.2 Two kinds of partial discharge signals

在仿真中 fc都取为 1 MHz，τ1、τ2、τ3分别为 2 μs、2 μs、4 μs，A1、A2都为 1 mV，采样频率为 10 MHz。

3.1 抑制平稳随机噪声

平稳随机噪声可用白噪声模拟。理想局部放电信号见图 3（a），加入白噪声（信噪比-2.029 0 dB）后的信号如图3（b）所示。

图3 局部放电仿真信号Fig.3 Simulateive partial discharge signals

本文基于STFT方法求取含噪信号的谱峭度。大量的试验表明在窗函数长度确定的情况下，窗函数的类型（如汉明窗、海宁窗等）对谱峭度的估计值影响不大；但窗函数的类型确定时，窗函数的长度对求取出来的谱峭度影响比较大。这是由STFT本身决定的，窗函数太长不能保证时间分辨率，窗函数太短不能保证频率分辨率，只能在时间分辨率和频率分辨率之间折中处理。所以本文考虑到局部放电信号本身的频率特征，选择的窗函数的类型为汉明窗，窗函数每次移动一个数据点，讨论窗函数长度为分别为25、45、85、125，求取含噪局部放电信号的谱峭度的优劣性，如图4所示。

图4 不同窗函数长度的谱峭度Fig.4 Spectral kurtosis for different window function lengths

窗函数长度为25时，谱峭度频率分辨率不高；窗函数长度为125时，谱峭度频率分辨率达到要求，但是其中包含很多噪声成分；窗函数长度为45和85时，频率分辨率达到要求，其中的噪声成分比较少。从而对含噪局部放电信号，选取窗函数长度为45～85。本文选择窗函数的类型为汉明窗，每次移动1个数据点，窗函数长度为55，求出的谱峭度如图5所示。

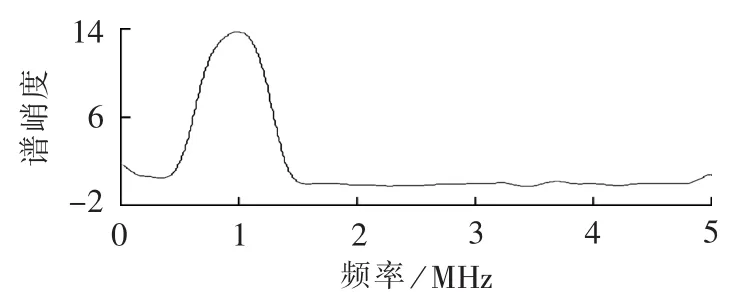
图5 谱峭度（窗函数长度为55）Fig.5 Spectral kurtosis（window function length is 55）

由局部放电信号的谱峭度可以确定局部放电信号的频率，而且加入的白噪声的谱峭度几乎为0，从而就可以通过局部放电信号和噪声的谱峭度大小来设计滤波器。

根据式（10）、（11）可以设计 Wiener最优带通滤波器，经过试验k的值使原信号谱峭度最大时，输出信号的峭度值最大，从而可得出最优带通滤波器，如图6所示，滤波后的信号如图7所示。

图6 自适应Wiener滤波器Fig.6 Designed adaptive Wiener filter

图7 滤波后的信号Fig.7 Signal after filtering

由图7可以看出，通过Wiener滤波器滤去了大部分噪声，能够清晰地看出局部放电信号的特征，但是还存在一些和局部放电信号频率相同或者相近的噪声信号。因此再进行小波平滑去噪处理，选用与本算例局部放电信号波形匹配较好的db8小波进行3层分解，就可以提取出光滑的局部放电信号。

分别用本文的方法和小波方法对局部放电信号进行去噪的结果比较如图8所示，小波方法的小波基选取的是与本算例局部放电信号波形匹配较好的db8小波，分解层数为8层。

图8 所提方法和db8小波方法去噪结果比较（信噪比为-2.029 0 dB）Fig.8 Comparison of denoising results between proposed method and db8 wavelet threshold denoising（SNR=-2.029 0 dB）

原始信噪比为-2.029 0 dB的含噪局部放电信号去噪后的性能指标[20]为消噪后的信噪比、均方根误差和相关系数。在表1中列出本文方法进行3层分解和db8小波进行3层、8层分解的去噪性能指标。

表1 所提方法和db8小波方法去噪性能指标比较（信噪比为-2.029 0 dB）Tab.1 Comparison of denoising performance between proposed method and db8 wavelet threshold denoising（SNR=-2.029 0 dB）

从图8和表1中可见，在原始信噪比为-2.0290 dB时，本文方法对平稳随机型干扰有很好的消噪效果，不仅大幅提高了信号的信噪比，而且失真度小，与理想局部放电信号的波形相似度最高。通过消噪后的信噪比、均方根误差和相关系数这几个指标的比较，明显看出本文方法比db8小波的各方面性能都要好。

为了体现本文提出方法在低信噪比条件下的处理性能，在信噪比为-7.926 1 dB的情况下与传统小波去噪进行了对比分析，结果如图9所示，各个性能指标对比在表2中列出。

通过在不同信噪比条件下，对本文提出的方法和db8小波阈值去噪性能的比较，可以得出db8小波只有在信噪比比较高且分解层数较大的情况下，对局部放电信号的去噪效果较好，然而分解层数越多，去噪后将丢失更多的原始信息，随着信噪比降低，db8小波的去噪性能明显下降，不能准确地提取出局部放电信号；而本文提出的方法先通过谱峭度设计出来的自适应带通滤波器，提高了信噪比，然后进行3层小波平滑去噪，分解层数少，保留了更多的原始信息，在信噪比较小时也能很好地对局部放电信号进行去噪，对局部放电信号的波形特征提取效果更好。

图9 所提方法和db8小波方法去噪结果比较（信噪比为-7.9261 dB）Fig.9 Comparison of denoising results between proposed method and db8 wavelet thresholddenoising（SNR=-7.9261 dB）

表2 所提方法和db8小波方法去噪性能指标比较（信噪比为-7.9261 dB）Tab.2 Comparison of denoising performance between proposed method and db8 wavelet threshold denoising（SNR=-7.9261 dB）

3.2 抑制混有白噪声的窄带周期干扰

窄带周期干扰可以通过一组频率不同的正弦信号表示，其频率 fc1、fc2、fc3、fc4分别设为 150kHz、500 kHz、1.75 MHz、2.5 MHz，干扰信号的数学表达式为：

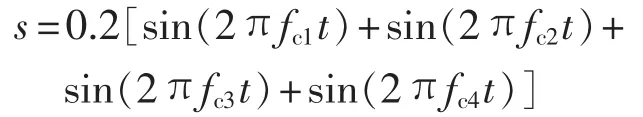
理想局部放电信号中加入窄带周期干扰和白噪声（白噪声是由MATLAB中自带常用白噪声功能函数产生），原始信噪比为-12.7138dB，如图10所示。

图10 含噪局部放电信号Fig.10 Partial discharge signals containing noises

窗函数的类型为汉明窗，每次移动一个数据点，窗函数长度为55，基于STFT谱峭度方法求出的谱峭度如图 11（a）所示。

根据图11（a）可以得出窄带周期干扰的谱峭度值接近-1，而白噪声的谱峭度值在0附近。利用本文提出自适应带通滤波器的设计方法，可设计出最优带通Wiener滤波器，如图11（b）所示。

图11 含噪局部放电信号谱峭度和自适应Wiener滤波器Fig.11 Spectral kurtosis of partial discharge signals containing noises and adaptive band-pass Wiener filter

对含噪局部放电信号进行滤波，再进行小波平滑去噪，得到去噪后的局部放电信号，如图12（a）所示；图12（b）为直接用小波去噪后的局部放电信号。

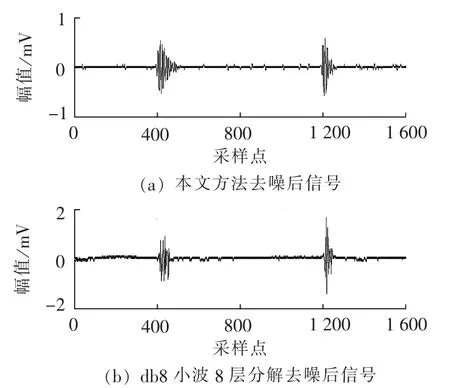
图12 所提方法和db8小波去噪比较Fig.12 Comparison of denoising results between proposed method and db8 wavelet threshold denoising

原始信噪比为-12.7138 dB的含噪局部放电信号去噪后的各个性能指标在表3中列出。

从图11和表3中可以看出，本文方法能对窄带周期型干扰有很好的抑制效果，不仅大幅提高了信噪比，而且失真度小，与理想局部放电信号的波形相似度最大。通过消噪后的信噪比、均方根误差和相关系数这几个指标的比较，明显看出本文方法比db8小波方法的各方面性能都要好。

表3 所提方法和db8小波方法去噪性能指标比较（信噪比为-12.713 8 dB）Tab.3 Comparison of denoising performance between proposed method and db8 wavelet threshold denoising（SNR=-12.713 8 dB）

4 结论

谱峭度是一个4阶累积量，属于高阶统计量，它不仅含有高阶统计量的良好抑噪性能，而且还能表征非高斯信号，确定其在频带上的位置。本文提出基于谱峭度的局部放电信号去噪方法，通过分析对平稳随机干扰和窄带周期干扰的抑制效果，并且与直接用小波去噪方法进行比较，得出本文方法去噪后的各个性能指标都优于小波方法，体现了本文方法良好的去噪性能，验证了该方法的有效性和可行性。