采用随机约束和多目标算法的电动汽车换电站能量管理

刘玉娇，蒋传文，王 旭，申景双

（上海交通大学 电气工程系，上海 200240）

0 引言

随着环境压力的增加和智能电网的发展，电动汽车迎来了良好的推广和发展机遇。对电力工业而言，电动汽车的普及不仅可以提高用电量，更可以给电网提供一些调频和调峰的资源[1]。电动汽车换电站通过提前给电池充电，然后通过为电动汽车更换电池的方式给电动汽车提供电池租赁服务。采用这种模式，电动汽车换电站不仅可以在与传统汽车在加油站相当的时间内完成电动汽车的电池更换，还可以采用小电流的均衡充电模式为电池充电，在有利于电池寿命的同时还可以为电动汽车提供快速服务[2]。因此，虽然电动汽车换电站的发展还受一些政策性的制约，如电池租赁价格的确定、电动汽车电池不统一等，但是电动汽车换电站的兴起可以使电动汽车的能源服务系统得到完善，极其有利于电动汽车的发展。因此针对电动汽车换电站的技术和营运模式的研究是非常有意义的。

市场环境下传统客户和其他形式的电动汽车充电模式的能量管理研究已经取得了很多的成果。文献[3]对大用户的长期购电策略进行了相关的研究，其提出通过多种购电方式组合来实现大客户的成本优化，并通过模糊决策实现考虑风险因素情况下的抉择。文献[4]对实时市场下的需求侧管理的风险进行研究，提出通过长期合约和期货保值的方式来规避实时市场的风险。文献[5]利用购电成本的期望和标准差的线性组合作为目标函数建立了考虑风险因素的大客户能量管理模型。文献[6]对大量电动汽车联合充电的问题进行研究，提出通过预设操作点的方法解决充电优化问题，其分析了联合充电对电动汽车和电网调频的好处。文献[7]探讨了让电动汽车在满足预设能量计划的基础上的充电优化。大规模电动汽车的联合调度要在基于所有电动汽车可以随时随地自由充放电并接受充电联盟调度的假设上进行，而电动汽车换电站内的电池随时充放电并被管理员控制，可以看作实现上述假设的方法之一。文献[8]就对含换电站的孤岛微网进行了能量优化的研究，得出换电站可以有效地减小微网的运行成本的结论。

整体而言，针对电动汽车换电站能量管理的研究目前还没有展开。为了在满足电动汽车换电需求的情况下尽可能地减小电动汽车换电站的运行成本，本文建立了电动汽车换电站的能量管理模型，并将风险管理的概念融入能量管理系统以解决电价的不确定性问题。本文所建的模型是以成本的期望和方差为目标函数的多目标、非线性和随机性的数学模型，这种模型的求解大都采用智能进化算法求解，如遗传算法、粒子群算法等[9-11]，本文采用多目标免疫克隆优化算法进行求解。此外，由于电动汽车的需求也是一个随机变量，因此模型采用一定概率下的随机约束来管理换电站对电动汽车的需求的满足程度。

1 电动汽车换电站能量管理模型

1.1 目标函数

电动汽车换电站的能量管理的主要目的是降低一定时间内购电成本，本文选定的时间管理周期为1 d，这样能量管理的目标函数为：

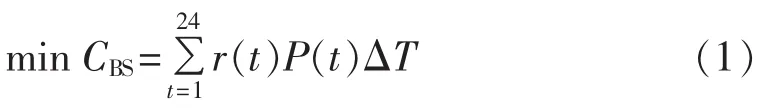
其中，CBS为换电站一天的成本；r（t）和 P（t）分别为 t时段内的电价和换电站充放电功率，充电为正，放电为负；ΔT为能量管理的最小时间段，本文选定为1 h。

式（1）描述了电动汽车换电站一天的成本。由于式（1）中的电价是未知的，因此式（1）实际是一个未知量，其无法直接作为目标函数使用，本文以其期望值为目标函数。考虑电价的波动性较强，期望值很可能会偏离实际值较大，因此仅采用期望值作为目标函数是不够的，必须对成本的风险加以衡量。金融管理中常用的风险定量方法有方差[12]、风险价值[13]和条件风险价值模型[14]。由于电价的时间相关性比较强，难以确定一定置信度下的风险价值或条件风险价值。本文选择均值-方差模型作为电动车换电站能量管理的风险度量方法。因此能量管理模型的目标函数为式（1）的期望和方差，如式（2）和（3）所示：

其中，P和rF分别为充电向量和预测电价向量；Cov（rF）为预测误差的协方差矩阵，根据预测误差的历史数据按照数理统计的方法获得[5]。

1.2 约束条件

电动汽车换电站的约束条件主要包括充放电功率极限约束、换电站储能容量约束和电动汽车换电需求约束，具体如下。

a.电动汽车充放电功率极限。

其中，Pmin和Pmax分别为换电站内所有电池的最大放电功率和最大充电功率，其值分别为单个电池最大放、充电功率Psmin、Psmax和换电站内电池数量N的乘积。

b.换电站储能容量极限约束。

由于电池的容量有限且不能为负，因此换电站的总能量也是受限的，如式（5）所示。

其中，Emax为换电站电池所含能量的最大值，其值为单个电池的最大容量Esmax和换电站内电池数量N的乘积；Eplan（t）为换电站所有电池在t时段所含的预计能量，计算方法如下：

其中，ES为每天开始之前换电站内所有电池储存的能量和。由于式（6）的计算过程考虑了t时段内的需求，式（5）可以保证换电站满足t时段的需求。

c.未来需求约束。

由于电动汽车换电站内的电池充电无法在一个时间段内完成由零电量到满电量的充电过程，因此换电站在t时段的操作要保证一定的储能容量来满足未来最短充电周期内的电动汽车换电需求：

其中，n=Esmax／Psmax为单个电池的充电周期，ED（t）为 t时段内电动汽车换电需求。

式（7）是为了避免发生在未来的j时段内即便换电站采用最大功率充电仍不能满足需求的情况。由于ED（t）至少为 k=R（ED（t）／Emsax）个电动汽车的需求，其中R（·）为向上取整函数，式（7）应该进一步严格约束为：

式（8）是保证j时段内至少有k个已充满电池的必要条件。由于Eplan（t）是一个不确定因素，因此式（5）和式（7）作为约束条件也难以直接用于求解过程中。本文将以上两式转换成一定可信度条件下的随机约束，如式（9）、（10）所示。

其中，α 和 β为所设定的可信度，式（9）和式（10）的左侧是电动车储能满足约束条件的概率。

2 基于多目标免疫克隆算法的求解流程

免疫克隆优化算法是近年来新兴进化算法之一，已经在许多工程领域取得较好的效果[15-16]。本文使用的基于Pareto准则的具体操作流程如下。

a.设定初始参数，并随机生成初始抗体群，本文采用实属编码，每个抗体是一个24维的向量：

其中，ai，t为t时段内电动汽车换电站的充放电的平均功率。

b.计算当前变异率和变异规模：

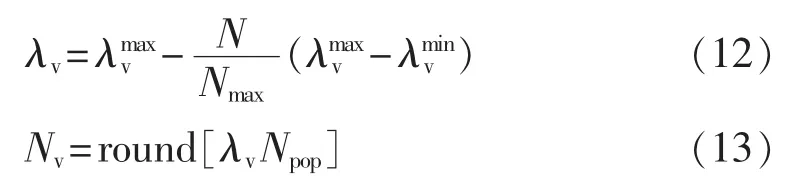
其中，λv、λvmax和 λvmin分别为当前、最大和最小变异率，N和Nmax分别为当前迭代次数和最大迭代次数，round为取整函数。

c.对所有抗体实施克隆操作。

d.对每一个克隆抗体，随机选取其一个元素按照式（14）和（15）进行变异。重复该步骤Nv次。

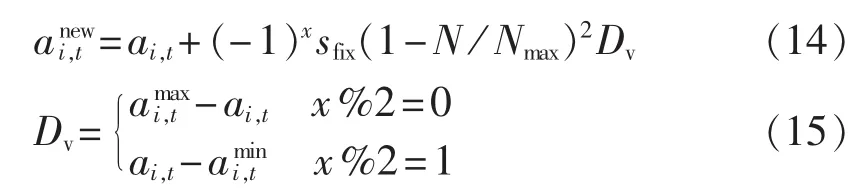
e.计算所有抗体的适应度值。

f.根据目标函数值挑选当前的Pareto前端集。

g.检查当前群体规模，若小于最小规模，则随机生成抗体补充至最小规模；若大于最大规模，则按照如下方式删除多余抗体。

（1）根据目标函数f1作降序排列。

（2）保存具有f1最大值和最小值的抗体，其他抗体的距离适应度值按下式计算：

（3）逐个删除距离适应度值最小的抗体，直至规模满足约束。

h.验证终止条件，若满足，则输出结果，否则转到步骤b。

3 系统控制策略

电动汽车的需求是一个随机变量，而且目前还没有具体的统计实例，因此本文根据一般预测系统的规律假设电动汽车的需求满足以预测值为期望的正态分布，则可通过如下步骤将式（9）和式（10）等价变换为确定性的约束。

a.由式（6），Eplan（t）是变量 ED（t）的线性组合，因此通过卷积可以求得其服从分布，其中：

其中，φ为标准正态分布函数。

b.未来需求约束变量 Enext（t）是变量 ED（t＋1）到ED（t+n-1）的线性组合，因此也服从概率分布，σ2next），其中：

结合 Eplan（t）的概率分布，将式（10）转换为确定性的形式如下：

4 仿真分析

电动汽车换电站的规模与其预计的年度或者月度的平均客流量和最大客流量有关，假设换电站电池规模为拥有300个可租赁电池，每个电池的容量为75 kW·h，单个电池的最大充电功率为25 kW，最大放电功率为-25 kW。这样单个电池的充电周期n=3 h，换电站整体的最大充放电功率为7500 kW。电动汽车换电站的需求预测如图1所示，为满足初始约束，设定换电站初始容量为300 kW·h。为验证模型有效性，分别假设电动汽车换电需求的相对预测误差服从 N（0，0），N（0，0.01）和 N（0，0.05），其中N（0，0）表示不考虑电动汽车换电需求的预测误差。

图1 电动汽车换电站的负荷需求和电价预测值Fig.1 Predictions of battery swap station power demand and electricity price

为了验证算法的有效性，本文选取3组电价分别作为能量管理模型的输入数据进行求解，数据如图1所示。算例仿真基于以上基本数据进行，算法参数如下：初始种群为100，克隆数为50，最大变异率为0.8，最小变异率为0.2。

不考虑电动汽车换电需求预测误差条件下基于不同电价数据的换电站的成本期望和方差如图2所示，图2中3组电价条件下算法都求解出了比较均匀的前沿解集，验证了算法的有效性。从图2还可以看出，不同预测电价条件下系统成本期望的最小值相差较大，但不同预测电价条件下的最小风险基本相同。

为了考察电价预测精度对成本期望和方差的影响，图3给出了基于电价数据1和不同电价预测精度下的成本期望和方差关系，其中为了更好地对比显示，方差坐标轴采用对数坐标。由图3可见，在预期成本相同的情况下，电价预测精度将决定电动汽车换电站所面临成本风险；不同预测精度下电动汽车换电站的最小预期成本基本是一样的。这是因为换电站的最小预期成本就是不考虑预测误差时的充放电计划，即在预测值相同的情况下，预测精度不影响最小预期成本，而预测精度相同的情况下，不同预测值将影响最小预期成本而不影响最小风险。

图2 不同电价的电动汽车换电站成本期望与方差Fig.2 Cost expectation and variance of battery swap station for different electricity prices

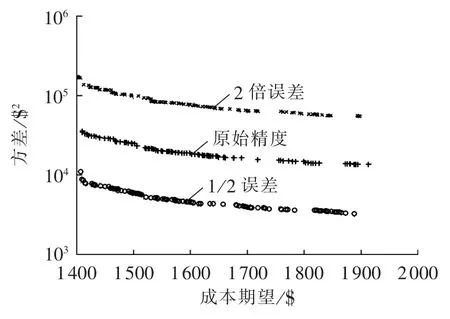
图3 不同电价预测精度条件下的换电站成本期望与方差Fig.3 Cost expectation and variance of battery swap station for different forecast accuracies of electricity price

选定随机约束的可信度为0.9，图4给出了在电价数据1和不同需求预测误差精度条件下的期望成本和方差的关系。由图4可以看到，电动汽车换电需求的约束对最小成本和最小方差都有影响，这是由于随机约束相当于对换电站容量极限的修正，如图5所示。图5是根据当前换电站容量和需求预测值，需求预测误差服从N（0，0.01）的条件下各时段最大最小容量的约束。图中置信度代表α和β的取值，由图5可知，随机约束的作用在于让换电站给出一定的储能容量备用来满足不确定的电动汽车换电需求，置信度越高对容量备用要求就越高。因此可以预见当置信度过高时，换电站可能无法满足电动汽车换电需求，这对换电站规模的规划是有借鉴意义的。

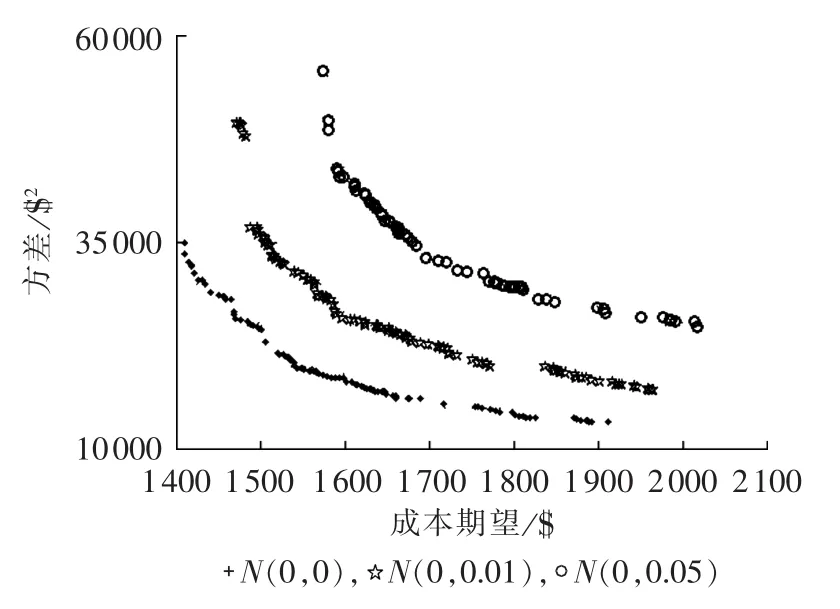
图4 不同需求预测精度条件下的换电站成本期望与方差Fig.4 Cost expectation and variance of battery swap station for different forecast accuracies of power demand

图5 不同置信度条件下的换电站容量约束Fig.5 Capacity constraints of battery swap station under different confidence levels

换电站的充放电优化在降低自身成本的同时可以给电网起到调峰的作用，假设所有电池在换下后立即充电的负荷为原始负荷，图6给出了不同条件下的电动汽车充放电计划和负荷转移量与电价之间的关系，其中负荷转移量为优化的充放电与原始充放电的差。从图中可以看出，最小成本计划的负荷转移量与电价基本呈负相关的关系，考虑电价与负荷需求之间的正相关性，可以认为负荷转移量与主网负荷之间具有一定的负相关关系。当选择风险较低的策略时，负荷转移的情况要相对保守，如当4 h出现负的预测电价时，最小期望成本的计划将充电功率放到了最大，而最小风险计划没有做出相同的安排。

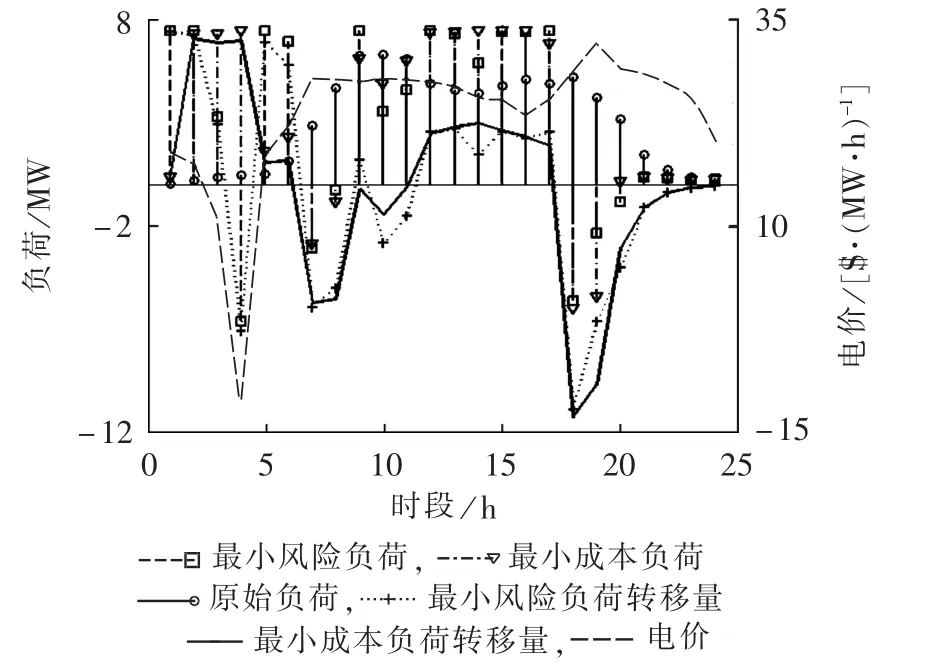
图6 不同条件下的换电站充放电计划Fig.6 Charge／discharge plans of battery swap station under different conditions

5 结论

在电动汽车快速充电受电池寿命约束的条件下，发展电动汽车换电站是普及电动汽车的重要手段之一，因为电动汽车换电站既可以满足电动汽车快速获取能源的需求，又可以采用小电流充电不伤害电池寿命。相比其他负荷，一般情况下电动汽车换电站将是自由度较高的负荷，其充放电时间不仅可以决定自身成本，对电网运行也有一定的影响。因此本文针对电动汽车换电站的能量管理问题进行研究，建立了考虑价格和需求不确定性的电动汽车能量管理多目标的模型，并使用多目标免疫克隆算法进行求解。算例仿真结果验证了算法和模型的有效性，优化后的充放电计划通过对原始负荷的转移在实现成本优化的同时可以提高电网的负荷率。通过本文所建的模型和求解方法，电动汽车管理员可以根据所能接受的风险大小和对成本的期望来选择合适的充放电计划。此外，通过对算例分析可知需求预测精度的约束实际上是限制了电动汽车换电站在不同时段内的最大和最小储能容量；而不同的电价预测精度则会造成电动汽车换电站在同一期望成本下具有不同的风险；不同电价预测值则对最小期望成本有着决定性的作用。