基于一种新的量化容差关系的变精度粗糙集模型

王金山， 王 磊

(解放军陆军军官学院数学教研室，安徽 合肥 230031)

粗糙集理论是一种能够定量分析处理不精确、不一致、不完整信息与知识的数学工具，由波兰华沙大学Pawlak(1982)首先提出，称为经典粗糙集理论。经典粗糙集理论研究的对象必须是完备信息系统，即论域中所有对象对应的属性值是已知的。但是在实际中，由于数据获取困难、容易丢失甚至数据本身就不存在等原因造成了数据缺失，称之为空值。这就造成了获得的信息系统是不完备的，称之为不完备信息系统。

为了使粗糙集模型能够处理不完备信息系统，学者们对经典粗糙集模型中的等价关系进行弱化，提出了更一般的二元关系，如容差关系、相似关系、限制容差关系和量化容差关系等。其中，使用最广泛的是由Kryszkiewicz(1999)提出的容差关系，它对不完备信息系统中对象间的相似性给出了定义，但对于相似程度没有定量度量而且容差关系的限制条件过于宽松，从而易将某些明显不相似的对象划分到同一容差类中。Stefanowski(2001)在容差关系基础上提出了量化容差关系，它利用己知信息的相同程度定量刻画样本对象间的相似程度，但对象间的相似程度量化的精确度不高。国内学者邓耀进等(2009)提出了一种新的量化容差关系，它利用统计分布代替概率分布得到了对象间的容差度，认为不同决策属性值对应的条件属性值的概率分布是相同的。然而，在一致决策表中，条件属性集中的属性取值不同就对应了不同的决策属性，反过来，决策属性取值也会对条件属性取值产生影响。对于某一条件属性而言，不同决策属性值对应的条件属性值的概率分布就可能不同，这会进一步影响容差度的计算结果。

同时，不完备信息系统中的空值是一种不确定的信息，也可以理解为噪声数据。空值的存在可能会对分类造成一定的影响甚至会造成错误分类的产生，因此利用具有一定噪声数据处理和错误分类容许能力的变精度粗糙集模型(Ziarko，1993)来处理不完备信息就非常有必要了。

本文在改进量化容差关系基础上考虑了策属性值对条件属性值概率分布的影响，建立了新的量化容差关系，在不完备信息表中已知信息充分的情况下，完全利用已知信息统计得到条件属性值的概率分布，建立了基于新的量化容差关系的变精度模型，提出了基于重要度的属性约简算法，最后通过实例说明了模型建立和计算的过程。

1 量化容差关系

定义1(官礼和，2009) 设S=(U，A，V，f)为不完备信息系统，对象集合X⊆U，属性集合B⊆A。设b∈B的值域为，则对于 ∀x∈U，f(x，b)=Vib的概率为1/|Vb|，其中|Vb|表示集合Vb的基数(此处为Vb中元素的个数)。

定义2(官礼和，2009) 对于∀x，y∈U，则x，y在属性集合B上取等值的概率(容差度)为:

其中pb(x，y)表示x，y在属性b上取等值的概率，其取值定义如下:

学者邓耀进等(2009)在量化容差关系的基础上提出了一种改进的量化容差关系。

定义3(邓耀进等，2009) 设对象集合X⊆U，属性集合B⊆A。设ci∈B，属性ci的值域为Vi=其中m=|Vi|。设tki表示属性值为的样本个数。

对于∀x，y∈U及∀ci∈B，则x，y在属性集合B上取等值的概率(容差度)为:

其中pi(x，y)表示x，y在属性ci上取等值的概率，其取值定义如下:

2 一种新的量化容差关系

新的量化容差关系的基本原则为:

(1)不完备信息表中已知信息充分，能够利用已知信息统计得到条件属性值的概率分布;

(2)若两个对象某属性值均为空值且决策属性值相同，则它们的条件属性值的概率分布相同，而且条件属性对应属性值中，空值等于次数出现越多的属性值的可能性越大;

(3)不管属性值是否为空值，对象与自身的容差度均为1。

设不完备信息系统 S=(U，A，V，f)，对象集合X⊆U，属性集合B⊆A。设ai∈B，属性ai的值域为，其中 m=|Vi|。

定义4 对于∀x，y∈U及∀ai∈B，则x，y在属性集合B上取等值的概率(容差度)为:

其中pi(x，y)表示x，y在属性ai上取等值的概率，其取值定义如下:

其中，P(Bj|Dr)表示当对象关于属性ai值为空且决策值为dr时，关于属性ai值为Vji的对象数与论域中关于属性ai非空且决策值等于dr对象数量的比值，即

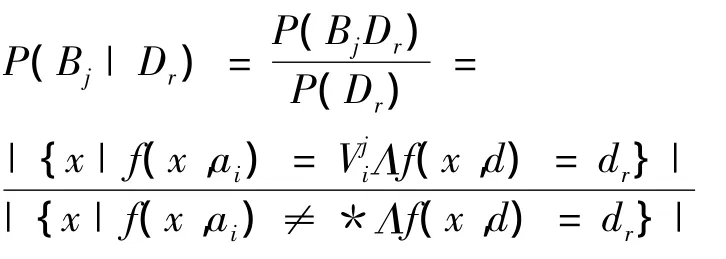
3 变精度粗糙集模型

定义5 量化容差关系定义为:

对象x的量化容差类IVTB(x)定义为:

定义6 设(U，IVTB)为近似空间，对于对象集合X⊆U，定义X基于改进的量化容差关系IVTB的β下近似集为:

定义X基于IVTB的β上近似集为:

定义X基于IVTB的β边界域为:

定义X基于IVTB的β负域为:

定义7 设U/d为决策属性d的等价类集合。

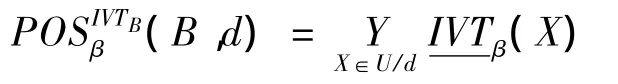
决策属性d与条件属性集B的β近似依赖性γ(B，d，β)定义为:

记C关于d的β近似约简为RED(C，d，β)，则RED(C，d，β)满足下面两个条件:

(1)γ(C，d，β)= γ(RED(C，d，β)，d，β);

(2)从RED(C，d，β)中去掉任何一个属性都将使(1)不成立。

定义8(文志信等，2011) 设属性c∈C－B，定义c相对于B的重要度SIGB(c)为:

SIGB(c)越大，说明在条件属性集C中属性c相对于决策属性d越重要。

定理1(米据生等，2004) 在条件属性集C中所有重要度不为0的属性构成C的核CORE(C)。

基于重要度的属性约简算法步骤如下:

(1)计算核CORE(C):对于∀c∈C，计算重要度SIGC(c)，所有重要度大于0的属性构成核CORE(C);

(2)令RED(C)←CORE(C);

(3)计算 γ(C，d，β)及 γ(RED(C)，d，β)并判断 γ(C，d，β)= γ(RED(C)，d，β)是否成立。若成立，则转(6)，否则转(4);

(4)对所有c∈C－RED(C)计算SIGRED(C)(c)并计算其中最大值，即

(5)令RED(C)←CORE(C)Y{cmax}，转(3);

(6)输出最小约简RED(C)。

4 实例

某投资公司现有10个备选投资项目，10个项目表示为论域X中的对象:X={x1，x2，…，x10};影响投资决策的属性有投资成本(a1)、预期收益(a2)、其他因素(a3)，则条件属性集 C={a1，a2，a3};决策属性为d。

其中，投资成本(a1)的属性值为高、中、低，分别赋值3，2，1;预期收益(a2)的属性值为高、中、低，分别赋值3，2，1;其他影响因素(a3)属性值为大、中、小，分别赋值3，2，1;策属性d属性值为不投资、投资，分别赋值0，1。具体数据见表1。

表1 投资数据表Table1

在表1中，属性a1，a2和a3对应的空值较少，已知信息充分，能够利用已知信息统计得到条件属性值的概率分布。

对于属性a1，假设有以下事件:

则有

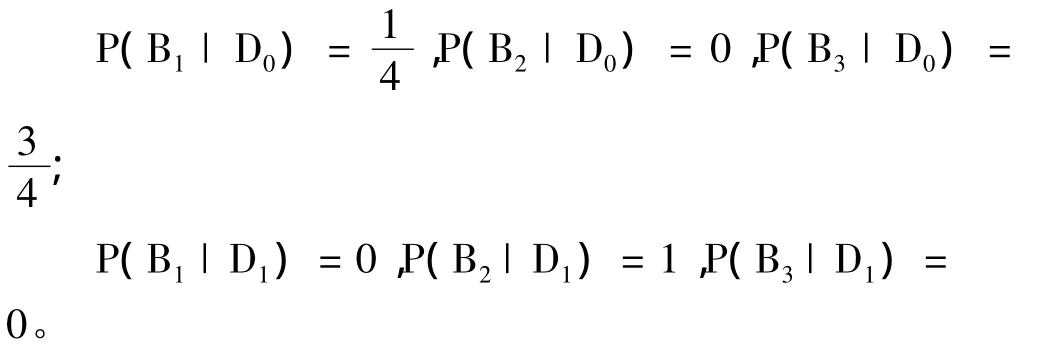
对于属性a2，假设有以下事件:

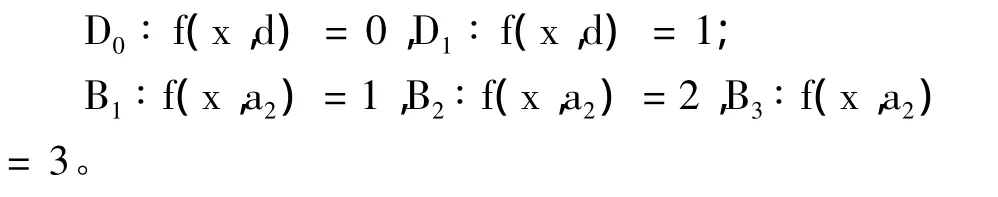
则有

对于属性a3，假设有以下事件:

则有

根据以上数据可以计算得到对象间关于C，{a1，a2}，{a1，a3}，{a2，a3}等属性集上的容差度。

下面利用基于重要度的属性约简算法进行属性约简。

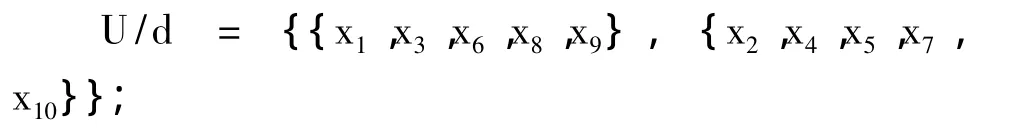
设 β =0.25，则有:

关于属性集 C，{a1，a2}，{a1，a3}及{a2，a3}的容差类集合分别为:

相对于决策属性d的β正域分别为:

β近似依赖度为:

进一步计算得到属性的重要度为:

可知核 CORE(C)={a1，a2}。

因为γ(C，d，β)= γ({a1，a2}，d，β)=1。所以{a1，a2}就是所求的约简。

5 结束语

本文提出了一种新的量化容差关系，充分利用了不完备信息表中的已知信息并且考虑了策属性值对条件属性值的概率分布的影响;建立了基于新的量化容差关系的变精度模型并提出了基于重要度的属性约简算法，使模型具有一定噪声数据处理和错误分类容许能力;最后通过实例说明了该模型能够处理含有空值数据的问题。

邓耀进，李仁发.2009.一种粗糙集理论中量化容差关系的改进[J].计算机工程与科学，31(10):105-108.

官礼和.2009.基于粗糙集理论的不完备信息处理方法研究[J].重庆邮电大学学报，21(4):461-466.

米据生，吴伟志，张文修.2004.基于变精度粗糙集理论的知识约简方法[J].系统工程理论与实践，24(1):77-82.

文志信，金栋，单洁.2011.基于条件嫡约简和粗糙集规则匹配的反辐射无人机作战目标威胁识别[J].舰船电子工程，31(6):68-72.

Kryszkicwicz M.1999.Rules in incomplete information systems[J].Information Sciences，113(3):271-292.

Pawlak Z.1982.Rough sets[J].International Journal of Computer and Information Sciences，11(5):314-356.

Stefanowski J.2001.Incomplete information tables and rough classifica-tion[J].Computaional Intelligence，17(3):546-564.

Ziarko W.1993.Variable precision rough set model[J].Journal of Computer and System Science，46(1):39-59.