基于sollin算法的含分布式电源的孤岛划分方法

曾令诚，吕 林，曾澜钰

（1.四川大学 电气信息学院，四川 成都 610065；2.中山市凯能集团有限公司电力技术服务分公司，广东 中山 528400）

0 引言

随着新能源的开发利用不断提高，在配电网侧将出现大量的分布式电源（DG），许多学者对配电网侧的孤岛划分进行了广泛而深入的研究。文献[1]以DG的额定容量为半径形成功率圆来进行孤岛的划分，但该方法具有局限性，如只适用于分散分布在配电网的小容量DG，且一个DG形成一个孤岛，开关操作次数较多。文献[2-3]主要是根据孤岛运行时的功率平衡要求进行孤岛划分，采用启发式的搜索策略实现，但其并未区分负荷的重要等级，所有负荷都是按照同一等级处理。文献[4]根据负荷情况分层逐级解列，并进行实时减载以保持功率平衡。文献[5]将配电网简化成具有节点赋权和边赋权的有根树，自上而下采用搜索加校验的方法实现DG的孤岛划分，但是该文献并未充分利用配电网的环网设计结构，均采用自上而下的辐射状结构，因此未能保证孤岛运行的最大化。文献[6]是目前较好的划分方法，该文献把对孤岛的划分转化成图论中的求最小生成树的问题，采用Prim算法实现，但该方法只适用于DG和负荷均接在母线上的配电网络，对于DG和负荷通过馈线接入配电网和含“T”节点的配电网络不再适用。文献[7-8]从微电网的角度对孤岛的运行、控制划分等问题进行了相关研究。文献[9]引入了可控负荷与不可控负荷的孤岛划分方法。

针对上述问题与研究现状，本文将进行以下研究：建模分析，将配电网模型按一定规则简化成树状模型；孤岛搜索与校验阶段，利用sollin算法求最小树实现孤岛的划分；对含DG的69节点配电网络和文献[6]算例进行分析，并与文献[6]算例进行比较。

1 含DG配电网的生成树模型

1.1 DG和负荷的接入方式

DG的接入分为2种：一是通过母线并入配电网，如图1所示的DG1通过母线4并入配电网；二是通过馈线并入配电网，如图1中的DG2通过连接在母线4的馈线并入配电网。

图1 含DG的配电网系统Fig.1 Distribution system with DGs

在配电网中负荷也有2种接入方式：一是直接与母线相连，如图1中的负荷L1、L2直接与母线2相连,负荷L3、L4与母线3相连；二是与馈线相连，形成“T”节点，如图 1 中的负荷 L5、L6、L9、L10接入馈线形成“T”节点。根据文献[9]负荷还可分为可控负荷与不可控负荷。

1.2 生成树模型

配电网都采用环网设计，开环运行。运行时呈辐射状网络，此时相当于一棵以电源为根节点的有根树，整个配电网相当于森林。这样就可以把含有DG的配电网简化成一棵节点赋权和边赋权的生成树T（V，E，W）[10]，其中 T 表示生成树；V 表示树的节点；E表示树的边，即节点之间的连接关系；W表示边的权值。基于上述特点可将故障下游的配电网简化成如下所述的生成树。

a.对节点负荷的处理：将节点负荷处理成“T”节点，把节点负荷上的功率引出一条由一个开关控制的负荷，该负荷的大小就是该节点负荷功率的大小，如此形成一个含“T”节点的电路，如图2所示。P1、P2和P3表示节点负荷上的功率。

图2 “T”节点负荷的形成Fig.2 Formation of “T” node load

b.把步骤a形成的含“T”节点电路转换成如图3所示的连通图：母线等效成母线节点，负荷等效成树枝（图3省略），馈线等效成树干。如果负荷含有可控负荷和不可控负荷，则将其划分成两部分负荷，具体划分参见文献[9]。待孤岛划分结束后将模型恢复到原先状态。图1所示的电路经简化后的模型如图3所示，图3中的每条边上的开关与负荷均已省略。

图3 包含DG配电网连通图Fig.3 Connection graph of distribution network with DGs

从图3可知，所有的DG和负荷都是接在母线2、3、4、5 或接在馈线 F1、F2、F3上，因此只要如图 3 所示的电路组成一个可连通的供电路径，则所有的负荷和DG都能够与该路径形成连通图，而这个供电路径就相当于图论中连通图的生成树。因此该问题就转化为求连通图中的生成树问题。

1.3 连通图边权值的确定

由连通图知识可知，节点集合V=｛vi｜0≤i≤n-1，n≥0｝，其中n表示节点数，其包含有DG节点、母线节点和负荷节点。vi表示节点i的数值：DG节点的数值是其发出的有功功率，为非负实数；负荷节点的数值是其所需的有功功率，为非负实数；母线节点无数值。边集合E=｛eij｜0≤i，j≤n-1，i≠j｝，边有以下3种形式：母线（或馈线）与DG相连的边；母线与母线相连的边；母线（或馈线）与负荷相连的边。权值集合W=｛wij｜0≤i，j≤n-1，i≠j｝，wij的值表示边eij的权值。权值设置得越小，说明在孤岛合并过程中越重要，即优先考虑动作，而其具体的数值大小没有实质意义，大小的不同只是区分其在路径选取中的重要程度。具体权值的确定方法如下[6]。

母线（或馈线）与DG相连的边的权值确定为0，因为要形成孤岛，首先在孤岛内必须有电源存在，因此把母线（或馈线）与DG的权值设置为最小值0，这样就能够保证在孤岛搜索过程中把所有的DG包含在孤岛内。

由图2可知母线与母线相连的边中包含有馈线、无任何电气设备的导线、安装有变压器的导线3种连接线，因此母线与母线相连的边的权值的确定原则有3种情况。

a.在有馈线的情况下，因为在馈线上接有负荷，为了保证馈线上的部分负荷供电，就得使馈线带电，因此将其设置为0，表明其优先权最高，保证其在孤岛搜索中被优先并入。

b.在无任何电气设备的导线的情况下，只相当于两母线间的连接线，中间没有接负荷，因此它的重要性不如情况a，即其权值要比a大，将其设置为 0.1（大于 0）。

c.在安装有变压器的情况下，由于变压器有损耗，因此在路径选取过程中与情况b相比时，将优先考虑情况b，因此此时的权值应比b还要大才符合要求（数值大于0.1）。但当变压器中含有二绕组变压器和三绕组变压器时，考虑到三绕组变压器的效率比二绕组的高，将优先考虑三绕组变压器，所以含三绕组变压器的权值要比二绕组小，在此设含二绕组变压器的权值为0.5，含三绕组变压器的权值设置为0.25。

母线（或馈线）与负荷相连的边的权值的确定原则为：为了减少开关的操作次数，将采用小负荷优先供电的方式来实现，同时还需考虑重要负荷优先供电的原则。因此其权值的确定将由负荷功率的大小和重要等级程度2个因素共同决定。其具体的权值计算公式如式（1）和式（2）所示[6]。 当按式（1）求出具有2个相同权值时，取重要程度高的负荷优先供电，此时能保证重要负荷优先供电。

其中，wij为母线或馈线与负荷相连边的权值；α、β分别为负荷功率大小和重要等级程度在权值中所占的比重，本文取α=β=1；Sj为节点负荷j的重要等级指标，取Sj=0，1，{}2 ，负荷j越重要，Sj的值就越小，即一类负荷对应Sj=0，二类负荷对应Sj=1，三类负荷对应Sj=2；Pmax为需进行孤岛划分范围内负荷的最大功率；Pmin为需进行孤岛划分范围内负荷的最小功率；Pj为负荷节点j的功率；Pij为负荷节点j的功率经标准化处理为1～10之间的数值。

在上述3种边的权值的设定中，把前2种边的权值设定为0～1之间的数值，是因为在孤岛搜索过程中，将其视为树干来处理，优先级较高；而把含负荷边的权值设定为1～10间的数值，是因为将其视为叶节点来处理，因此优先级比前者低。

2 孤岛划分的数学模型

基于上述连通图模型的建立，本文采用如下孤岛划分的数学模型：

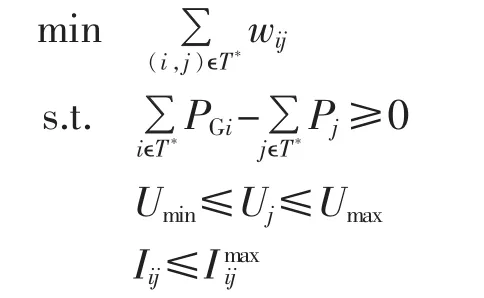
其中，T*为所求得的最小生成树；PGi为最小生成树中DG的有功功率，Pj为最小生成树中负荷的有功功率，由于无功功率不适宜远距离传输，均采用就地补偿的方式，因此不考虑；Uj为节点j的正常电压，Umin、Umax分别为节点 j允许的电压下限、上限；Iij、Imijax分别为线路eij允许的正常电流和最大允许电流。

目标函数是求最小生成树，即权值最小。第1个约束条件是保证孤岛内的有功功率平衡，以全网的平衡为目标，由于无功功率可通过在负荷侧增设电容补偿装置调整，因此不考虑；第2个约束条件是孤岛内各节点电压不能越限，将其限制在0.95～1.05的额定电压范围之内；第3个约束条件是孤岛内各线路流经的电流不能越限。

3 sollin算法求最小生成树

由第2节的目标函数可知，其目的是要在连通图中寻找一棵权值和最小的生成树，即最小树。因此本文将采用sollin算法[11]求解其最小树，具体步骤如下。

a.对N中任意一个节点i∈N，N表示所有节点的集合，定义

b.如果T*中已经有n-1条弧，则T*为T的最小生成树；否则对T*中的所有子树节点集合Nk（k∈N），计算边割[Nk，／Nk]中的最小弧，即计算 w（e*k）=｛min w（e）｜e∈[Nk，／Nk]｝。 其中 ／Nk表示 Nk补集，e*k=（ik，jk），ik∈Nk，jk∈／Nk。

c.对T*中的所有子树节点集合Nk及最小弧e*k=（ik，jk），将该子树与 jk所在的子树合并成一棵子树，如。果有相同的最小弧则取ik+jk小的边。并令T*=T*∪｛（ik，jk）｝，然后转至步骤 b。

具体流程图如图4所示。

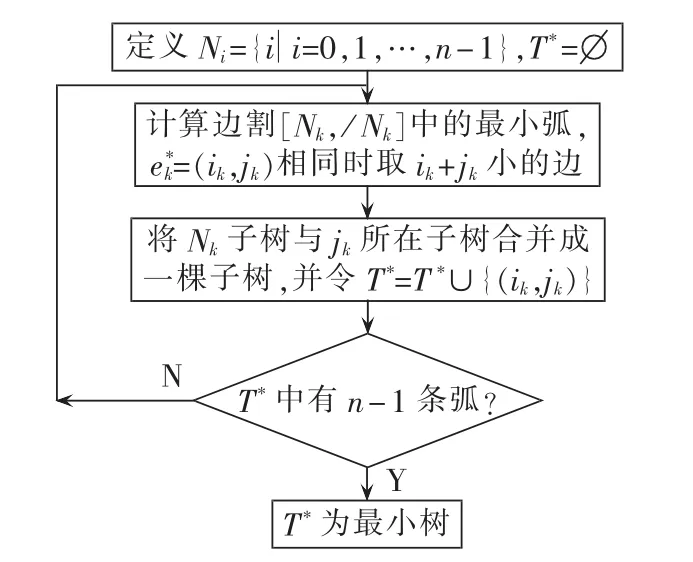
图4 sollin算法流程图Fig.4 Flowchart of sollin algorithm

4 孤岛划分策略

由第1节所介绍的含DG配电网的简化模型可知：母线节点始终是树状模型的内点，负荷作为生成树的末梢节点，馈线作为树枝。由图论知识可知：任意删除两内点相连的边将使整棵树拆分成2棵子树，从而有可能导致部分子树失电；删除一条树枝，将影响与该树枝相连的所有叶节点的供电。末梢节点（叶节点）的删除只影响该末梢节点，不会影响到其他节点的供电。因此可以先以内点（母线节点）作为节点和馈线作为树枝求解出一棵最小生成树，然后再把DG合并到所求出的最小生成树上，最后以负荷作为叶节点，在满足功率平衡的条件下按权值由小到大的顺序并入该最小树。

具体过程如下。

a．以母线作为树的节点，利用sollin算法求出最小树 T*（V*，E*），并把未加入的馈线放入边集合 E*中，因为由图2可知：馈线连接在两母线之间，由于权值为0，所以加入了该树中；馈线只连接在一条母线上，对此本文将其直接加入该树中。此时所求得的最小树中V*均表示母线节点，E*表示母线与母线相连的边和馈线。

b．把需进行孤岛划分区域的DG全部并入最小树 T*（V*，E*），并计算即把孤岛内所有DG功率相加。此时V*包括母线节点和DG节点，E*包含母线与母线相连的边、馈线和母线与DG或馈线相连的边。

c．负荷按权值由小到大的顺序排列，若有相同权值的负荷，重要程度等级高的排在前面。从权值最小的负荷开始，将负荷依次并入树 T*（V*，E*）中，每次并入一个负荷，并计算P=P-PLi，其中PLi表示刚并入树T*（V*，E*）中负荷 Li的功率。 并且判断 P是否大于等于0，若是，继续并入下一个负荷按该步骤依次进行下去，直到P≤0或所有的负荷都搜索完毕时停止。

d．优化孤岛。 对上述所求得的最小树 T*（V*，E*）进行优化，去除没有与负荷相连的母线节点或馈线，并对其进行潮流分析计算，检测是否满足约束条件。若线路过载，则充分利用环网结构，投入一条支路分流过载线路；若母线电压越限，则在母线投切电容器进行调节。

按孤岛划分策略，图1的最小生成树如图5所示，具体的流程图如图6所示。

图5 最小生成树图Fig.5 Chart of minimum spanning tree

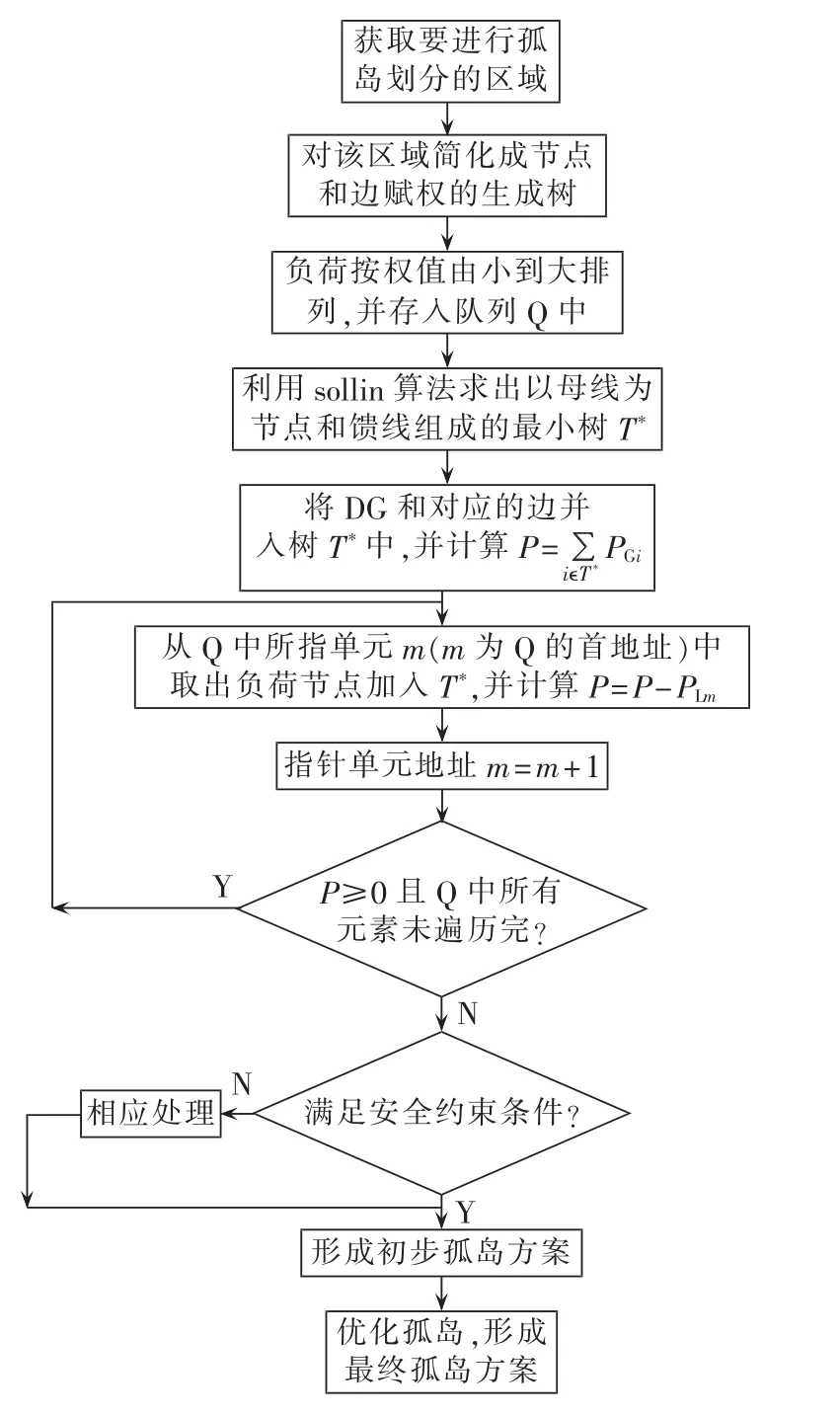
图6 孤岛划分算法流程Fig.6 Flowchart of islanding algorithm

e.执行完上述步骤后，最终形成的树 T*（V*，E*）就是配电网故障后的孤岛方案，闭合树 T*（V*，E*）内的所有开关和断路器，跳开树 T*（V*，E*）以外的所有开关和断路器，此时孤岛已经形成。同时利用孤岛检测技术[12-14]对其进行检测，看是否成功形成孤岛，并将信息反馈至调度中心。

5 算例分析

如图7所示69节点配电系统，其中节点49和节点50含有40%的可控负荷，其余各参数与文献[6]相同。经该文献的划分可得一个最大的孤岛，即断开节点61的全部负荷，节点49和节点50可控负荷部分恢复供电，其优点是只有一个孤岛，开关操作次数最小，只需断开一个负荷。经潮流检验，图7所示为最终孤岛[15-16]。

图8为文献[6]所示的某一含DG的典型配电系统利用本文孤岛划分方案所得的最优孤岛划分方案，图中DG与负荷功率单位均为MW。其中开关6、7、23、44、59、65、72 所接的负荷为一类负荷；开关 5、21、33、70所连负荷为三类负荷；其余为二类负荷。开关21所接负荷中有1／3的可控负荷；开关80所接负荷中可控负荷占1／8。经潮流检验得最终的孤岛运行如图8所示，切除了开关5、16、52、70所接负荷；开关21、80所接可控负荷全部恢复供电（分别为 0.37 MW、0.4 MW）。

对比文献[6]可得如下结论。

a.本文方法能够适应DG和负荷通过馈线接入的配电网系统，并且对于不同电压等级和只含同一电压等级配电网系统均可划分。而在算例图7中文献[6]就不适用。

b.sollin算法的核心思想是开始把所有的点处理成独立的树，形成一个森林，根据边割最优条件，把各子树（森林）逐渐地合并成一棵树。由于这是子树与子树间的合并，因此搜寻速度将成倍递增，极大地缩短了搜索时间；而文献[6]所采用Prim算法求最小树时，其思想是首先选择一棵树，然后根据边割最优条件，逐个节点和逐个边加入该树中，这样慢慢地扩大这棵树。显然，对于多节点的大配电网系统而言，采用本文所提出的sollin算法将能节省大量的计算时间。

c.文献[6]在进行最小树的搜寻时要进行3次Prim算法计算，而在本文中由于只是寻找一棵关于母线节点的最小树，因此只要运行1次sollin算法即可实现，进一步缩短了时间。

d.文献[6]可恢复的负荷功率为18.38 MW，由于引入了可控负荷和不可控负荷，因此本文算法可恢复18.42 MW的负荷功率，与文献[6]相比，提高了DG的利用率。

图7 含DG的69节点配电系统Fig.7 69-bus distribution system with DGs

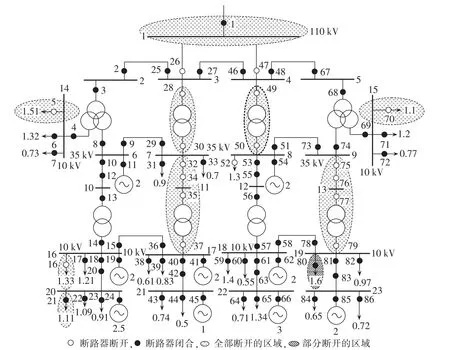
图8 文献[6]含DG配电网的孤岛划分方案Fig.8 Islanding scheme of distribution system with DGs in reference[6]

6 结论

孤岛的划分是为了实现当配电网发生故障时，充分利用故障下游的DG，按一定规则继续给故障下游负荷供电，以提高用户的可供电持续率。因此本文结合现阶段方法的优点，在考虑负荷重要等级和可控负荷与不可控负荷的情况下，忽略无功（无功采用就地补偿），以有功功率平衡为约束条件将配电网划分成求最小生成树模型，实现孤岛的划分，并与已有划分方法进行比较分析。通过算例分析表明：

a.该算法不仅能够适用于不同电压等级的配电网，及同一电压等级的含馈线的配电网络，同时还适用于负荷和DG通过不同方式接入的配电网络；

b.通过引进可控负荷与不可控负荷，一定程度上提高了DG的利用率；

c.利用sollin算法的快速收敛性，有效地提高了计算速度；

d.采用全网求最小树所得的孤岛是一个最大的孤岛，开关操作次数少。

本文也存在一定的缺陷，因在某些情况下配电网的边际条件会发生改变，如重要负荷的变化等，而文中只利用负荷平衡作为唯一的约束条件，显然在这些配电网络中不够合理，后续的研究将予以解决。