电网电压矢量定向的三相异步电机同步切换控制策略

徐 友，刘永超，郑建勇，华 伟

（1.东南大学 电气工程学院，江苏 南京 210096；2.南京农业大学 工学院，江苏 南京 210031；3.重庆电力设计院，重庆 401147；4.苏州自来水公司，江苏 苏州 215002）

0 引言

大中城市自来水厂和污水处理厂的提升泵房通常配有3台以上大功率水泵，其中仅1～2台配置变频装置，每台水泵电机功率通常在500 kW（有的甚至在2 000 kW）以上。根据使用要求，提升泵组有时需要2～3台水泵同时工作。变频装置控制水泵缓慢（软）启动，电机启动电流较小（通常为稳态电流的2～3倍），机械冲击小，而如果是直接合闸的硬启动，其启动瞬时电流通常为稳速电流的10倍以上，因此大功率水泵硬启动不仅机械冲击大、易磨损，而且对局部电网会产生较大的冲击，影响附近用电设备正常运行和局部电力供应安全。

泵房仅配置1台变频器，只能对1台水泵进行变频控制。当需要2台及以上水泵同时工作时，变频器先变频启动一台水泵，当水泵电机启动至额定转速时切换至电网供电，变频器再对下一台水泵电机进行变频软启动[1]。如果采取直接切换或是异步切换[2-3]，会对电网产生较大的电流冲击，因此必须检测变频器输出电压和电网电压相位实现电机的变频-工频同步切换[2-3]，克服大功率水泵变频-工频直接切换或是异步切换带来的机械冲击大、易磨损以及对局部电网产生瞬时冲击的弊端。

因此，开展大容量三相异步电机的变频-工频切换的控制策略和电路拓扑对实现电机软启动和平稳切换、减小电网冲击电流、抑制电机转矩突变和提高电机使用寿命具有积极意义。国内外相关专家及业内人士对此展开了大量的分析和研究。

文献[4-12]采用锁相环技术控制变频器输出电压和电网电压的某一相或某一线电压同步实现大功率电机变频-工频的平稳切换；文献[13]采用鉴相鉴频器实现大功率电机变频-工频的平稳切换。根据锁相环工作原理，锁相环稳定运行时无频率差，但是存在一定的相位误差，因此基于锁相环技术的电机切换控制器难以实现零相位差切换；在电网电压不是严格对称或电网电压波形发生畸变的工况下，变频器输出电压和电网电压的某一相或某一线电压同相难以确保电机切换时变频器电压和电网电压在空间上保持相位一致，进而无法实现真正意义上的同步切换；同时，针对目前普遍采用的交流接触器存在开关延时较大的问题，必须重新考虑并设计新型的切换开关以减小切换延时，以最大限度地减小电机切换时对电网的冲击电流。

鉴于以上分析，本文提出一种基于电网电压空间矢量定向的电机变频-工频同步切换的控制策略，并给出在电网电压矢量同步坐标系下检测变频器电压相位的方法，可以精确捕获变频器电压矢量与电网电压矢量在空间上相位相同的时刻，提高同步精度，最大限度地降低变频-工频切换对电网的电流冲击；并且提出采用电力电子开关与交流接触器并联工作的新思路，可解决交流接触器开关延时对切换控制精度的影响；最后设计了基于DSP控制的电机变频-工频同步切换的实验系统。实验结果证明了理论分析和研究的正确性和有效性。

1 三相异步电机定子瞬间断电暂态分析

三相异步电机定子瞬间断电时，定子电流和电磁转矩立即变为0，转子则成为无源闭合电路，根据断电瞬间转子磁链不能突变的原则，由于定子开路无法励磁，因此转子中立即产生励磁电流，在定子断电后电机内电枢反应停止，转子电流成为自由分量，从断电瞬间的初值按转子时间常数以指数规律衰减。

设定子在t1时刻断电，定子电流iX=0（X=A，B，C），转子的三相电压方程为：

其中，Rr为转子每相电阻，Lr为计及相邻两相的互感作用后的感应电机转子每相总自感。

根据式（1）可知转子三相电流为：

其中，τr为转子回路的时间常数，τr=Lr／Rr；Ix为转子各相电流初值。

定子断电后电磁转矩变为0，则电机的转速在负载转矩的作用下逐渐降低，其机械角速度Ωr以指数规律降低[14]。

转子中的直流分量将在定子绕组中产生一角频率为ωr的感应电动势，则：

其中，p为电机的极对数。

因此定子端的感应电势的频率同样以指数规律降低。

根据以上分析，电机定子断电后，由于转子中的励磁电流呈指数形式衰减，转子磁链的幅值也以指数规律衰减；转子的机械角速度呈指数规律衰减，感应电势的频率也以指数规律衰减，感应电势的波形也并非正弦波，且随时间推移发生较大的畸变。

当电机重新投入电网时，在电网电压与感应电势的共同作用下，将对电网产生一定的冲击，其大小取决于电机重新投入电网时电网电压与电机定子侧感应电势的相位差。因此为减小电机变频-工频切换对电网的电流冲击，在切换时要遵循以下2个原则：电机在切换至电网前，变频器输出电压应与电网电压相位保持一致[14]；因电机定子断电后，感应电势的幅值、频率、相位相对于电网电压迅速衰减，波形也会发生畸变，应尽可能缩短切换时开关动作的延迟时间。

2 电网电压定向的变频器输出电压相位同步检测方法

根据电机学理论，变频器输出电压空间矢量与电网电压空间矢量同相时，电机切换对电网产生的冲击电流最小，而在电网并非严格对称时，仅是两者的某一相电压同步或是某一线电压同步并不等价于两者电压空间矢量同步，此时切换无法将电网的冲击电流降至最低。本文采用电网电压矢量定向的方式捕捉变频器输出电压空间矢量与电网电压空间矢量相位相同的时刻，以获得最佳切换时刻，实现同步切换。

三相电压可以用一个旋转矢量在相隔120°的3根时间轴上的投影表示，这个可同时表示三相的电压量的旋转矢量称为电网电压矢量[15]。设电网三相电压为：

其中，Em为电网相电压幅值，ω0为电网电压角频率，φ0为电网A相相电压初始相位。

引入旋转算子a=ej120°，则电网线电压的综合矢量为：

根据式（5）可知电网电压矢量的瞬时相位为：

将电网三相电压变换到以电网电压矢量的瞬时相位定向的同步旋转坐标系（dq坐标系），可得：

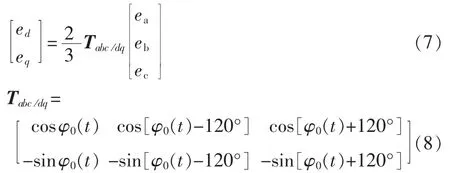
其中，Tabc／dq为电网电压矢量定向的同步旋转变换矩阵。

根据式（7）可以得出变频器输出线电压在dq同步旋转坐标系下的直轴分量ud和交轴分量uq：

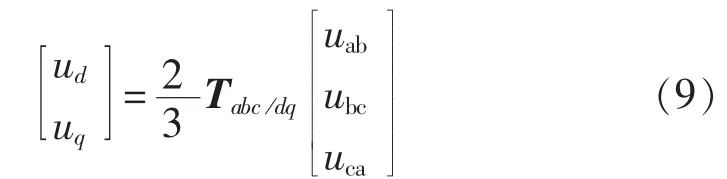
其中，uab、ubc、uca为变频器输出线电压，则变频器输出线电压空间矢量为：

电网电压和变频器电压的矢量关系如图1所示（图中将C轴缩短表示）。

图1 电网电压和变频器电压矢量图Fig.1 Space vectors of grid-voltage and transducer-voltage

切换控制系统采集变频器的线电压，由于线电压超前相电压30°电角度，因此切换时变频器电压矢量应在dq坐标系下处于30°位置，如图1中虚线位置，通过变频器输出电压的直轴分量ud和交轴分量uq判断变频器电压矢量是否位于图1中虚线位置，进而判断变频器电压和电网电压是否同相，即：

在工程上，由于存在数据采集误差和DSP有限精度的限制，式（11）可表示为：

3 电网电压定向的同步切换控制系统

电机变频-工频同步切换控制系统如图2所示，其中KM1、KM3分别是电网侧和变频器侧的交流接触器，KM2、KM4分别是电网侧和变频器侧的电力电子开关，KM1、KM2并联连接，KM3、KM4并联连接；系统分别采用3个霍尔电压传感器采集电网侧相电压ea、eb、ec和2个霍尔电压传感器采集变频器侧的线电压 uab、ubc，并对变频器侧的线电压 uab、ubc进行低通滤波处理，其中：

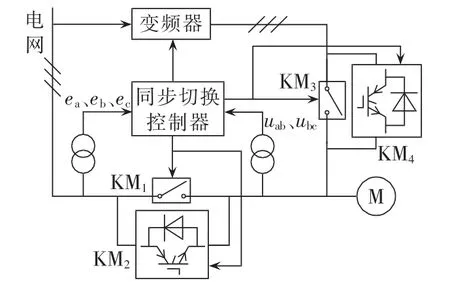
图2 电机同步切换控制系统Fig.2 Control system of motor synchronous switching

根据电网侧霍尔电压传感器测得的电网三相电压 ea、eb、ec，并由式（5）计算得到电网电压空间矢量E，由于E是一复数，可根据其实部和虚部计算得出电网空间电压矢量 E 的瞬时相位 φ0（t），即式（6）；再根据布置在变频器侧的霍尔电压传感器测得变频器输出的线电压 uab、ubc、uca，并由式（9）即可计算得到变频器空间线电压矢量在以电网电压矢量定向的dq同步旋转坐标系下的直轴分量ud和交轴分量uq。为实现差频同相切换[16]，在电机同步切换前将变频器输出频率调整至51 Hz，则变频器空间线电压矢量相对于dq同步旋转坐标系以2πrad／s的相对角速度（1 rad／s）旋转，同步切换控制系统以 12 kHz的采样频率对电网三相相电压和变频器三相线电压进行采样，并实时计算变频器空间线电压矢量在dq同步旋转坐标系下的直轴分量ud和交轴分量uq，当ud和uq满足式（12）时，变频器线电压空间矢量位于图1中的虚线位置，此时即为电机进行同步切换的最佳切换时刻。

同步切换控制系统中切换开关的开关动作时间对系统的影响较大，一般交流接触器的开关延时为0.1 s左右，约为5个工频周期，在这段开关延时时间内电机速度因负载的不同，其变化差异很大，若不采取改进措施，极易引起两者相位偏差大而导致电机切换时形成瞬时大电流冲击。为避免交流接触器的开关延时对系统的影响，本文采用绝缘栅双极型晶体管（IGBT）和电力二极管设计了全控型电力电子开关，物理结构如图3所示，A、B端子用于串接在交流电路中控制交流电路的开通和关断，IGBT集电极和发射极分别连接在二极管桥式整流电路直流输出端的正极和负极，其中，R、C为电压尖峰吸收网络，以防止IGBT关断时被高压击穿。切换信号控制IGBT的栅极电压以控制IGBT的开通和关断，当IGBT开通时，由于整流桥直流侧短路，A、B端子的等效电阻为0，A、B端子中流过交流电流，即处于交流闭合状态；当IGBT关断时，由于整流桥直流侧开路，A、B端子中的交流电流即被切断，A、B端子处于交流开路状态。根据以上分析可知，切换信号可控制A、B端子所串接的交流电路的开通和关断。

图3 电力电子开关电路拓扑Fig.3 Topology of electronic power switch

电机在变频器激励下运行时，变频器侧的交流接触器KM3和电力电子开关KM4均处于闭合状态，电网侧的交流接触器KM1和电力电子开关KM2均处于断路状态。电机需要切换至电网时，同步切换控制器通过通信接口控制变频器的输出电压频率略高于电网频率（一般为51 Hz）至电机运行于稳态，保持电力电子开关KM4导通，给交流接触器KM3发送触发信号控制其断开，等待0.1 s确保KM3完成开关动作后，同步控制器通过AD采集电网和变频器的电压数据，根据以上提出的同步检测方法捕获最佳切换时刻。在切换时刻，控制器先关闭KM4，延时50 μs以提供死区时间，然后同时触发KM1和KM2使其导通，由于KM2开通时间不超过1.5 μs，因此KM2先于KM1导通，约0.1 s后，交流接触器KM1完全闭合，将KM2短路，KM2中的电流即为0，因此电机切换成功并进入稳态运行后，电力电子开关电流为0，无需进行散热处理，节省了空间和成本。同时根据以上控制过程，交流接触器KM1、KM3的近似零电压开通和关断，均不会产生电弧，提高了系统的安全性。

4 实验结果

为验证理论分析和研究的有效性，本文以TMS-320F28335 DSP为核心在实验室设计了同步切换控制系统，对一台功率为4 kW、极对数为2的三相异步电机进行了变频-工频切换实验，电机通过联轴器与测功机和测速发电机相连接，测功机负载转矩设置为25 N·m。在此实验系统的基础上，本文对基于电网电压定向的电机同步切换控制策略进行了实验研究，并对单一采用交流接触器和采用电力电子开关与交流接触器并联的切换方式进行了对比实验，实验波形如图4所示。

图4 电机同步切换实验波形Fig.4 Experimental waveforms of motor synchronous switching

由图4（a）和（b）可见电机切换至电网时形成较大的电流冲击，冲击电流为稳态电流的5倍左右，电机转速下降较多；由图4（c）和（d）可以看出电机切换至电网时没有出现大的冲击电流，冲击电流的峰值约为稳态峰值的2倍左右，由于采用电力电子开关，电机切换至电网时对电网的电流冲击大幅减小，电机速度变化较小，在发生较小幅度的振荡后逐步进入稳态；由图4（e）和（f）可以明显看出电机切换至电网时对电网的电流冲击大幅减小，冲击电流的峰值进一步降为稳态峰值的1.2倍左右，电机速度变化较前两者更小，基本消除了电机切换至电网时对电网的电流冲击，电机切换前后转速在发生轻微波动后快速进入稳态。

5 结论

本文针对三相异步电机在进行变频-工频切换时会对电网形成较大电流冲击的问题，提出了一种基于电网电压矢量定向的同步控制策略，综合考虑电网三相电压的相位和幅值信息，研究了在电网电压矢量定向的同步坐标系内变频器输出电压的相位检测方法，确保电机切换时刻变频器输出电压空间矢量和电网电压空间矢量的相位取得一致，最大限度地降低电机切换时对电网的电流冲击；同时，以本文提出的电力电子开关与交流接触器并联工作的新思路构建的实验系统，实测结果表明可将变频-工频开关切换延时缩短至50 μs左右，仅为目前广泛采用的单一交流接触器切换方式延时时间的0.05%，由此可大幅提高变频-工频切换的控制精度，同时也增强了该切换控制系统对于不同电机和负载的适应性，并从根本上消除了切换电弧，提高了设备和局部电网的安全性。