从瞬变电磁扩散场到拟地震波场的全时域反变换算法
2013-10-08戚志鹏孙怀凤杨增林
戚志鹏,李 貅*,吴 琼,孙怀凤,杨增林
1 长安大学地质工程与测绘学院,西安 710054
2 山东大学岩土与结构工程研究中心,济南 250061
1 引 言
瞬变电磁拟地震成像是实现瞬变电磁三维反演的有效手段,其中关键问题之一是实现由瞬变电磁扩散场到虚拟波场的转换.只有进行了波场逆变换,才有可能实现基于波动方程的电磁法拟地震解释.
所谓的电磁法拟地震解释主要有三种,第一种是根据电磁波在导电介质中和地震波在弹性介质中传播的相似性以及反射函数表达式之间的一致性把地震勘探中的一些基本方法应用于电磁测深资料解释.主要成果有:Levy(1988)根据弹性波与大地电磁场之间的类比性,获得了与反射地震类似的拟反射函数的脉冲响应时间断面图,将大地电磁资料用线性规划技术对一维和简单的二维地电断面进行了成像计算,并推导了直流问题的拟脉冲响应函数[1];王家映根据电磁波在导电介质和地震波在弹性介质中传播的相似性及其反射函数表达式之间的一致性,在国内率先提出了对大地电磁资料进行拟地震解释的方法和思路[2-5];郭文波、薛国强等基于中心回线装置观测成果与MT成果的一致性,借助大地电磁拟地震解释,进行了TEM拟地震成像解释[6-7].第二种是借助偏移成像的广义概念在扩散场条件下实现电磁偏移.主要成果有:前苏联学者Kjahos吸取了“偏移成像”的广义概念,在电磁法中确立了正则偏移和解析延拓偏移两种方法[8-10];Zhdanov等[11-13]借鉴了地震勘探中的逆时偏移概念,对时间域的瞬变电磁场和频率域的大地电磁场进行了逆时偏移成像的深入研究,提出了偏移电磁场的概念,并且建立在逆时偏移电磁场基础上对二、三维反演问题也开展系列研究.第三种方法是基于Lavrent′ev(1980)的研究即瞬变电磁扩散场与虚拟波场之间存在着准确的数学变换关系,实现扩散场到波场的变换,在虚拟波场的条件下引入地震勘探处理和解释的一些基本理论进行电磁成像[14].主要成果有陈本池、李金铭等利用奇异值分解实现瞬变电磁波场变换,利用有限差分进行二维瞬变电磁拟地震成像解释[15-16];李貅等对瞬变电磁时间信号进行了分段处理,结合正则化算法分段实现了瞬变电磁波场变换,利用Kirchhoff积分实现了瞬变电磁三维曲面延拓成像[17-21],并基于此开展了提高虚拟波场分辨率的系列研究[22-24].但是,目前这方面的研究在算法和方法适用性方面仍存在不少问题.在对复杂介质进行大地电磁拟地震解释时遇到一些困难,如电磁波速度求取问题;基于扩散方程的逆时偏移成果仅限于单个或者多个孤立异常体的成像;利用扩散场到波场的变换关系可以实现复杂介质的成像,但是由于波场反变换方程是第一类Fredholm积分,属于典型的不适定问题[25-27],李貅等早期研究为了降低问题的病态程度,采取了时间分段手段,有效降低了矩阵的病态程度,但这也引入了段与段的衔接问题[18,20,28].
本文在李貅教授原有的研究基础上进行瞬变电磁的波场变换算法,采用预条件正则化共轭梯度法实现全时域的波场变换算法,既有效避免了分段,又实现了由扩散场到波动场的变换.利用虚拟波场可以在波动方程下进行虚拟波场偏移成像.
2 波场变换的基本原理
早在1972年,Kunetz[29]在对大地电磁解释和反演问题的研究中发现,电磁场满足的扩散方程与波动方程之间具有相似关系.随后,Lavrent′ev于1980 年,在 《Ill-posed problems of mathematical physics and analysis》一书中对扩散方程与波动方程之间的对应关系进行了深入研究,并给出了两个方程之间准确的数学变换关系式[14].Lee在1987年与1989年的研究成果中又进一步证明了这种数学变换适用于任意的场分量[30-31].
在导电介质中,忽略位移电流,瞬变电磁场满足扩散方程.为了不失一般性,取f(x,y,z,t)为瞬变电磁场的电场或磁场分量函数,其满足的扩散方程如式(1)所示:

其中μ为介质磁导率,σ为电导率.引入函数U(x,y,z,τ),其满足波动方程如式(2)所示:
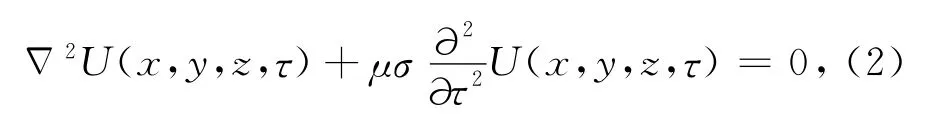
根据文献[14,16,21,29]可知,由扩散方程到波动方程转换的对应关系表达式为

(3)式为第一类Fredholm型积分方程,由扩散场求波场是典型的不适定问题.将其离散后得到的线性代数方程组是病态的,且随着阶数的增加,矩阵条件数急剧增大,病态性更加严重,因此必须选用可靠的离散方式和稳定的数值方法.本文采用预条件正则化共轭梯度法实现波场反变换的计算[32-33].
3 波场变换的数值离散

计算式(4)的关键是如何选取一组τj(j=1,2,…n)以及对应的一组wj(j=1,2,…n)使其最好的满足式(4).对于虚拟时间与积分系数的选择,文献[18,20]通过给定的特殊积分,根据两步最优化选定一组最优的虚拟时间和一组最优的积分系数.但是
将式(3)进行离散,写成数值积分形式文中矩阵A的条件数较大,矩阵方程严重病态.虽然如此,我们仍可以借助特殊积分选取合适的离散方式,提取最优的虚拟时间τ和最优的积分系数w.
我们对比了一些常规的离散方式,如等间距离离散,对数等间距离离散,等面积离散和高度等间距离离散四种方式,得到不同离散方式的虚拟时间分布示意图(图2).根据不同离散方式选取虚拟时间,采用数值积分方法进行积分,比较各数值积分精度和离散后各矩阵条件数,结果如表1所示.通过比较选取均方误差最小,形成系数矩阵条件数最好的等间距离散.
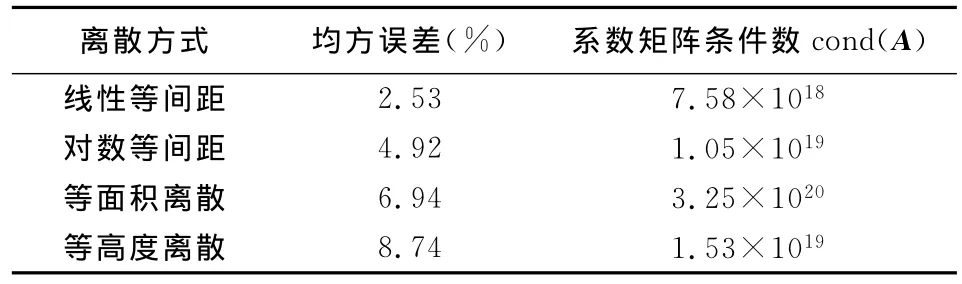
表1 不同离散方式比较Table 1 The comparison of different discrete method
4 预条件正则化共轭梯度法实现波场反变换
考虑到文中方程组系数矩阵较大,单纯的正则化共轭梯度法(RCG)或者预条件共轭梯度法(PCG),都不能很好地解决问题.因此,将两种方法相结合形成预条件正则化共轭梯度法(PRCG).由于在实际应用当中主要采集磁场的垂直分量,因此文中以磁场垂直分量为例进行分析.
将式(4)写成矩阵形式为

其中A= [aijwj]m×n,系数矩阵A包含积分系数wj,U=[uj]n×1为虚拟子波,F=h[]im×1为接收的瞬变场时间信号.

图1 不同时间道的核函数展布图(a)0.000001~0.0001s时间范围;(b)0.1~10s时间范围.Fig.1 Kernel functions at different times

图2 不同离散方式虚拟时间分布示意图(a)等面积离散;(b)对数等间距离散;(c)高度等间距离散;(d)线性等间距离散.Fig.2 The time display with different discrete way(a)Equal area discrete;(b)Logarithmic equal space discrete;(c)Equal altitude discrete;(d)Linear equal space discrete.
为了利用共轭梯度迭代,将式(5)转化为
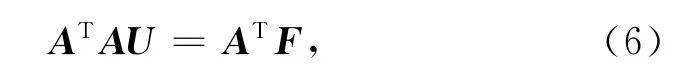
只要A是列满秩矩阵,ATA就是对称正定矩阵,因此可以利用共轭梯度法.但是ATA的条件数较A的条件数更大,使方程的病态更加严重.
为了进一步降低矩阵的条件数,改善方程的病态程度,在进行正则化共轭梯度之前,对系数矩阵进行预条件.对于预条件矩阵的构造采用超松弛预条件法,这是因为对称超松弛预条件是一种较为有效的预条件方法,不仅预条件子容易求得,而且有效降低矩阵的条件数[34-37].数学上已经证明经过超松弛预条件后,矩阵条件数降为原来的平方根[36].

设矩阵可分解为
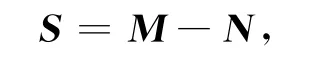
其中

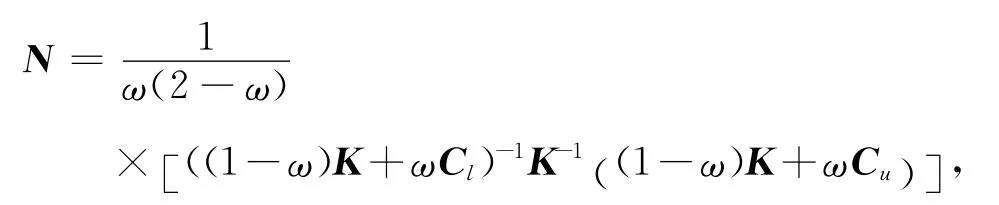
K,Cl和Cu分别为S的对角元、下三角元和上三角元,ω为(0,2)内的参数.于是我们可以选择预条件矩阵P如式(7)所示:
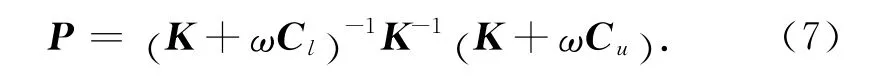
假设根据矩阵A(v)构造的预条件子为M(v),构造新的方程如式(8),矩阵M(v)-1A(v)接近单位阵,因此迭代很快收敛.具体计算过程如图3所示,其中kmax为外层循环最大迭代次数,ε为正则化共轭梯度法迭代终止条件,lmax为内层循环最大的迭代次数,ξ为内层共轭梯度迭代终止条件,v为选定的正则化参数.

其中,xk为第k次迭代的x值;x的初值x(0)选为单位向量;A(v)=vI+ATA.
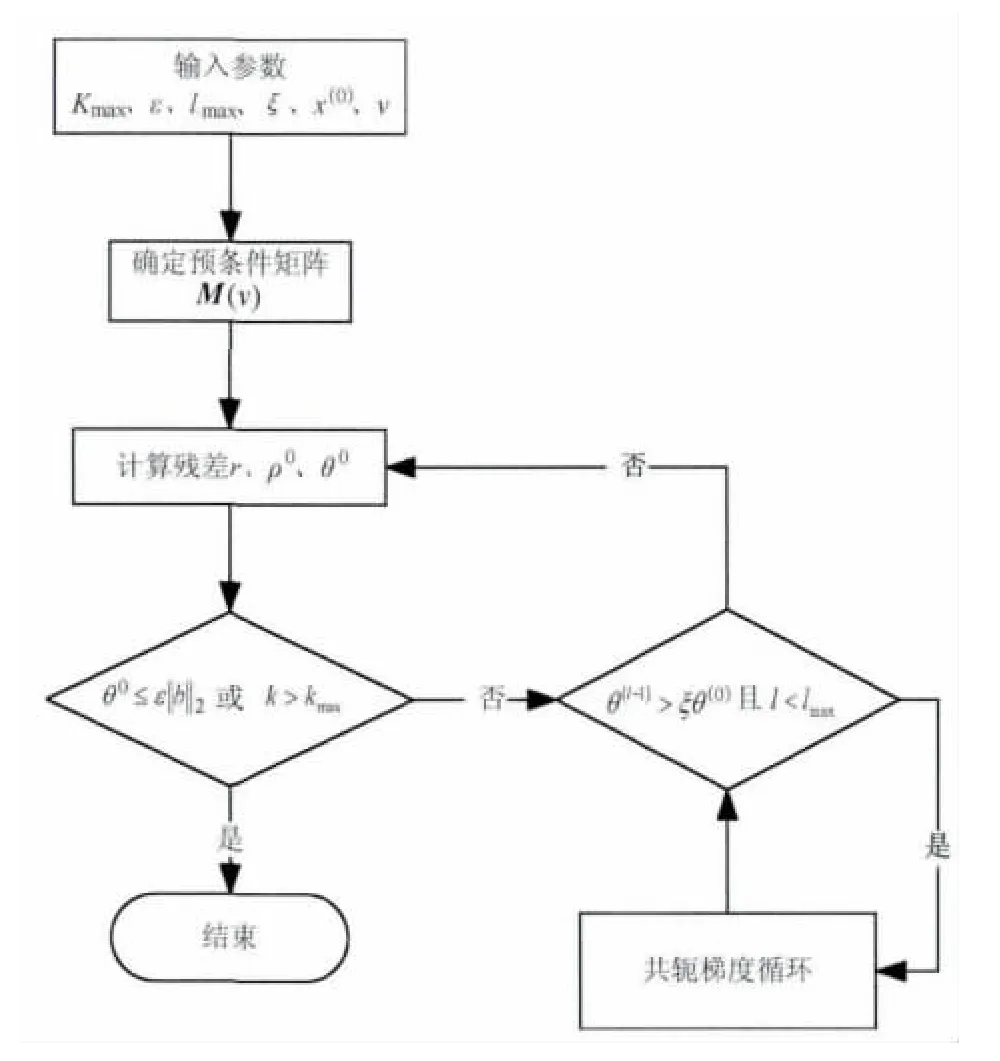
图3 预条件正则化共轭梯度法计算框图Fig.3 Computer block diagram of PRCG method
正则化参数v的选择非常重要,正则化参数v(δ)使U在近似性与稳定性之间进行优化选择.Zhdanov等[38-39]提出正则化因子不断递减的自适应算法.并与L曲线法做了比较,认为采用自适应算法所得反演结果不逊于L曲线法所得结果,由于L曲线法需要通过多次反演计算来确定最佳的正则化因子,计算量将成倍增长,而自适应算法只需在每次迭代前确定参与当次反演的正则化因子,因此可以大大减少计算时间.在文献[40]中,王彦飞依据偏差原理提出了重开始共轭梯度法(RSCG)计算最佳正则化因子,并与CGNR和CGER方法进行比较,认为RSCG方法更加稳定[40].正则化方法在大的电磁反演中已有广泛的应用,如文献[41-44]等均利用正则化方法实现了大地电磁反演,并给出了相应的正则化因子的确定方法.但是,瞬变电磁场较大地电磁场时间范围与动态范围均更广,不适定性更加严重,不能简单地引用大地电磁反演中使用的正则化方法.
经分析,文献[40]中所述的方法更适合本文情况.因此,文中依照文献[40]重开始共轭梯度(RSCG)计算方法,根据部分先验信息来选择最优的正则化参数值.正则化因子v为一渐变的量,其初始值v0为数据拟合泛函与稳定泛函的比值,在前期大量模拟计算的基础上基本可以确定正则化参数的初值,根据经验可以取v0等于0.00005为分段最大的正则化因子.在此后的迭代过程中,如果数据拟合残差随迭代次数逐渐变小,正则化因子可保持不变,否则按照(9)式进行选择:

上式中ξ为经验系数,有ξ>1,k表示预条件正则化共轭梯度(PRCG)的迭代过程中第k次迭代.
在完成积分离散以及正则化参数选择后,对方程(4)式运用预条件正则化共轭梯度法进行求解计算.取波场理论值为U(x,y,z,τ)=1,这时方程为一简单积分,求得函数值H(x,y,z,t)=表2所示为适用时间区间[0.000078,0.006280]的正则化参数.利用(PRCG)法求得反变换结果如图4a所示,最大误差小于2%,可知文中所述方法满足要求.

表2 正则化参数估计结果Table 2 Regularization parameter estimation result

图4 利用PRCG与RCG方法实现的波场反变换结果(a)利用PRCG方法获得的波场反变换结果;(b)利用RCG方法求得的波场反变换结果.Fig.4 Comparison wave-field inverse transform result with PRCG method and RCG method(a)The wave-field inverse transform result of synthetic wave records with PRCG method;(b)The wave-field inverse transform result of synthetic wave records with RCG method.
为了便于比较,给出采用正则化共轭梯度法(RCG)获得的反变换结果,如图4b所示.比较图4a与图4b可知,采用预条件处理后,正则化参数可以选取较小(v=0.0011285)就能达到很好的收敛效果;不采用预条件处理,正则化参数选择较大时(v=0.008),其收敛效果尚不如采用预条件技术的结果.由此可知预条件处理是必要的.
众所周知,正则化参数需要在稳定性与分辨率之间平衡,正则化参数越大,分辨率越低.为了进一步说明问题,现给出同一模型两种方法的波场变换结果,且两方法选择的正则化参数一致,为v=0.003,如图5所示,图5a为采用PRCG方法获得的波场变换结果,图5b为采用RCG方法获得波场变换结果.由图可知模型具有两个电性分界面,且两个界面之间为一薄层,采用预条件正则化共轭梯度方法的结果可以分辨出薄层以及两个电性界面,而正则化共轭梯度方法获得的波场结果不能区别出两个界面.由此可以说明,文中所述的PRCG反变换方法比RCG方法的分辨率高.
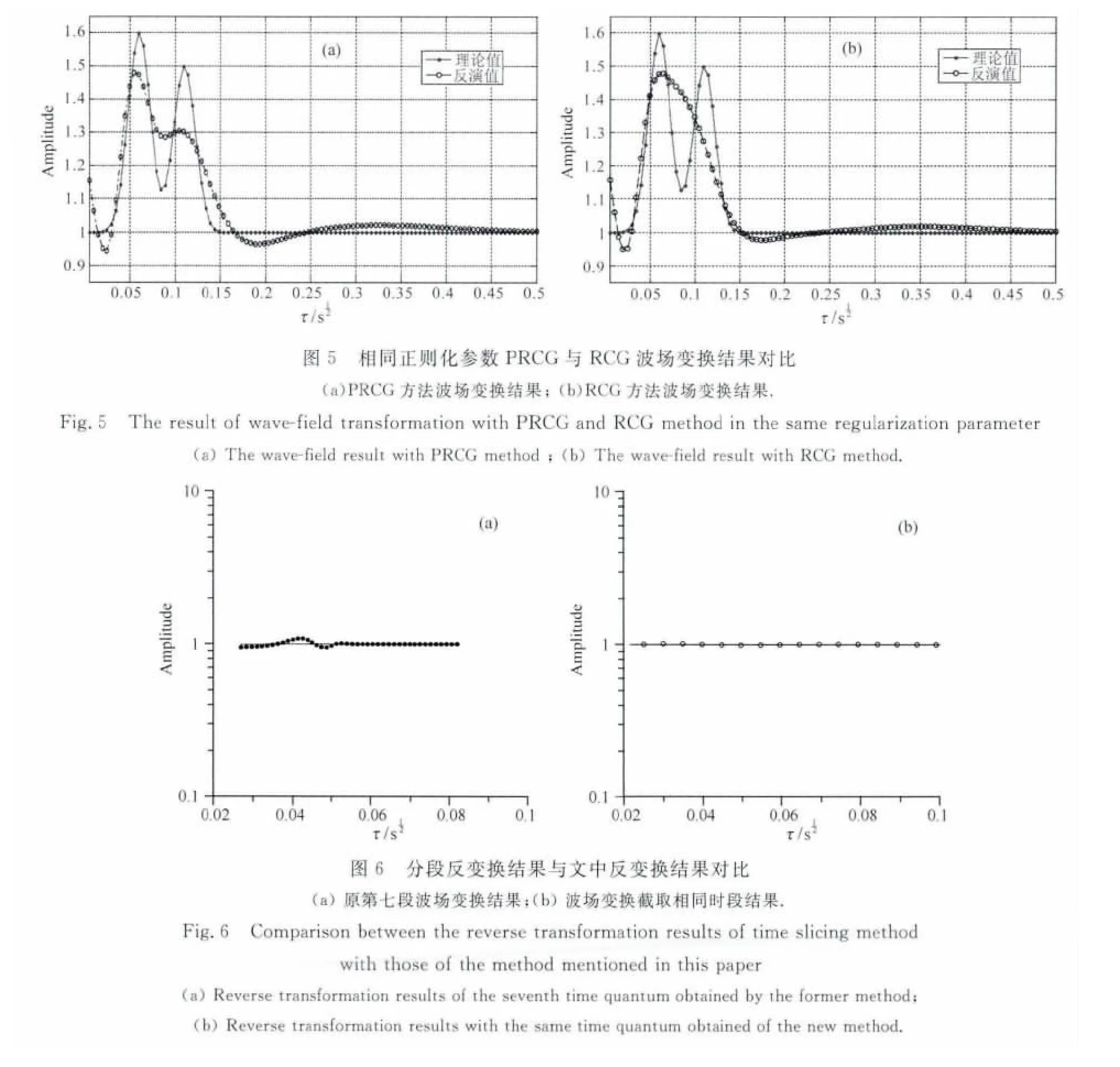
文献[45]中,张军、李貅(2009)等对不同时刻进行了分段,为了便于比较,截取相同时段计算结果与其进行对比,如图6所示.对比可知,在相同时段内,本文方法计算精度高于分段正则化算法精度.
5 瞬变电磁虚拟波场分析
5.1 不同地电模型波场变换响应
上文根据特殊子波对方法进行了验证,说明方法的正确性.为了验证方法对复杂介质的适用性,利用文中波场变换方法分别对两层模型和三层模型响应进行波场变换分析.瞬变电磁响应反映地下介质的电阻率分布情况,当介质为高电阻率时信号衰减较快,当介质为低电阻率时信号衰减较慢.根据瞬变电磁衰减信号的特征,我们可以判断层状介质的电阻率相对变化情况.以高斯脉冲为子波给出虚拟波场值,通过式(3)可以获得与之对应的瞬变电磁衰减信号,并判断地下介质电阻率分布情况.根据瞬变电磁衰减信号可知,含有一个子波的为两层模型,含有两个子波的为三层模型,且子波为正表示下层电阻率较上一层电阻率低,子波为负表示下层电阻率较上一层电阻率高.
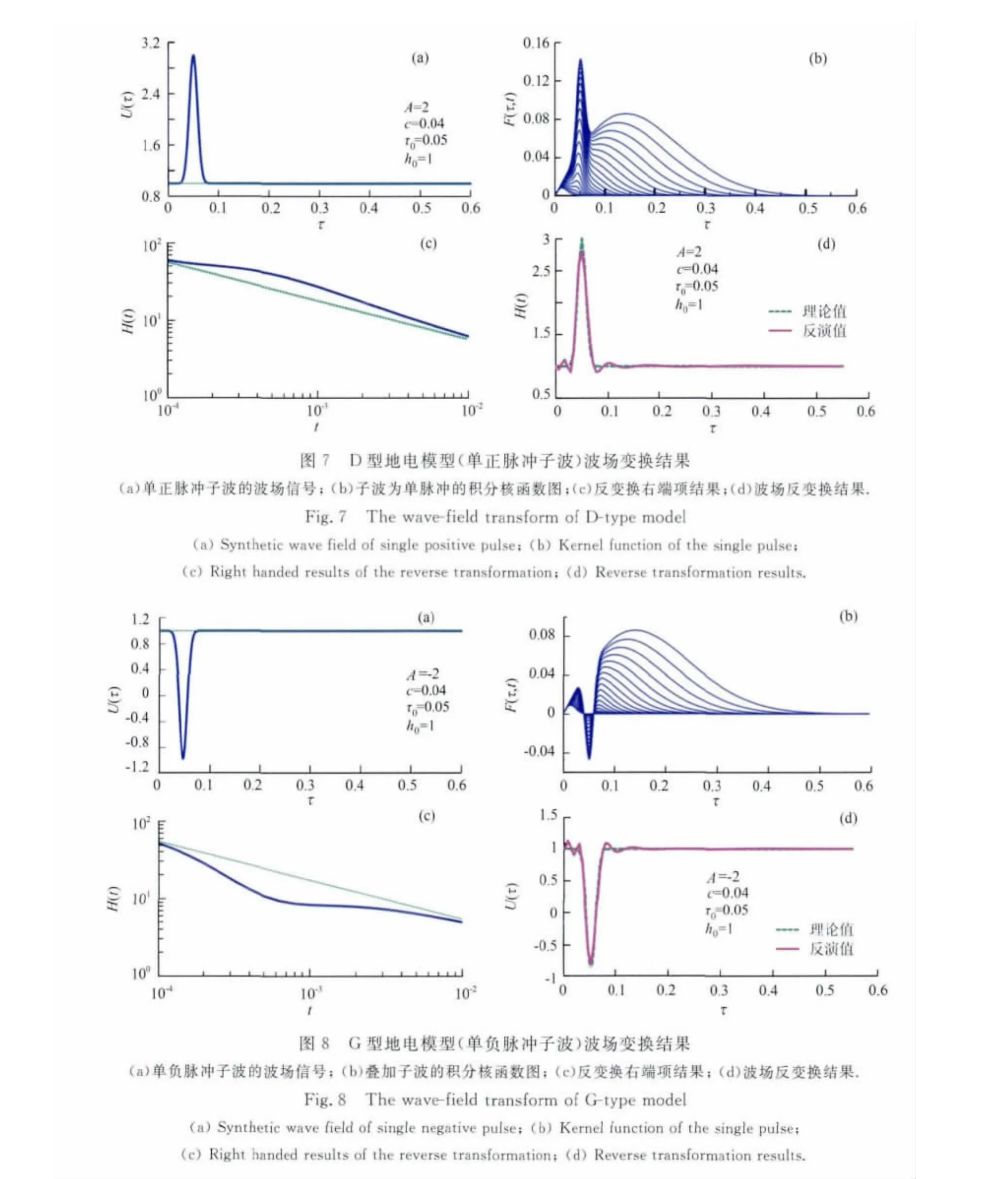
根据特殊子波U(x,y,z,τ)=1可以确定正则化参数的合理范围.选择正则化参数后,对给定的地电模型进行模拟.对两层模型的反变换结果如图7、8所示,由图可知,反变换所得波场与已知虚拟波场基本吻合.
三层模型的波场反变换结果如图9、10、11、12所示,由图可知,反变换结果与已知波场基本吻合,说明方法适合于复杂介质.图中第二波峰较第一个波峰振幅有很大衰减,子波宽度略有增加.这与波在有耗介质中的传播规律相符,从而证明了算法的正确性.另一方面,模型的反演结果充分说明了瞬变电磁方法对浅部异常分辨率较高.随着深度的增加,电磁波高频部分损失严重,响应主要为低频响应,因此对深部异常的分辨率降低.
5.2 含噪信号的波场变换分析

野外测量数据受各种因素影响难免会有干扰,因此有必要研究含噪信号的波场变换.文中以单脉冲响应的波场变换为例进行分析,加性噪声分别为1%、2%、3%、5%.如图13、14、15、16所示为不同信噪比的D型模型时域响应信号和与之对应的波场变换结果;图17、18、19、20为不同信噪比的G型地电模型时间域响应和与之对应的波场变换结果.
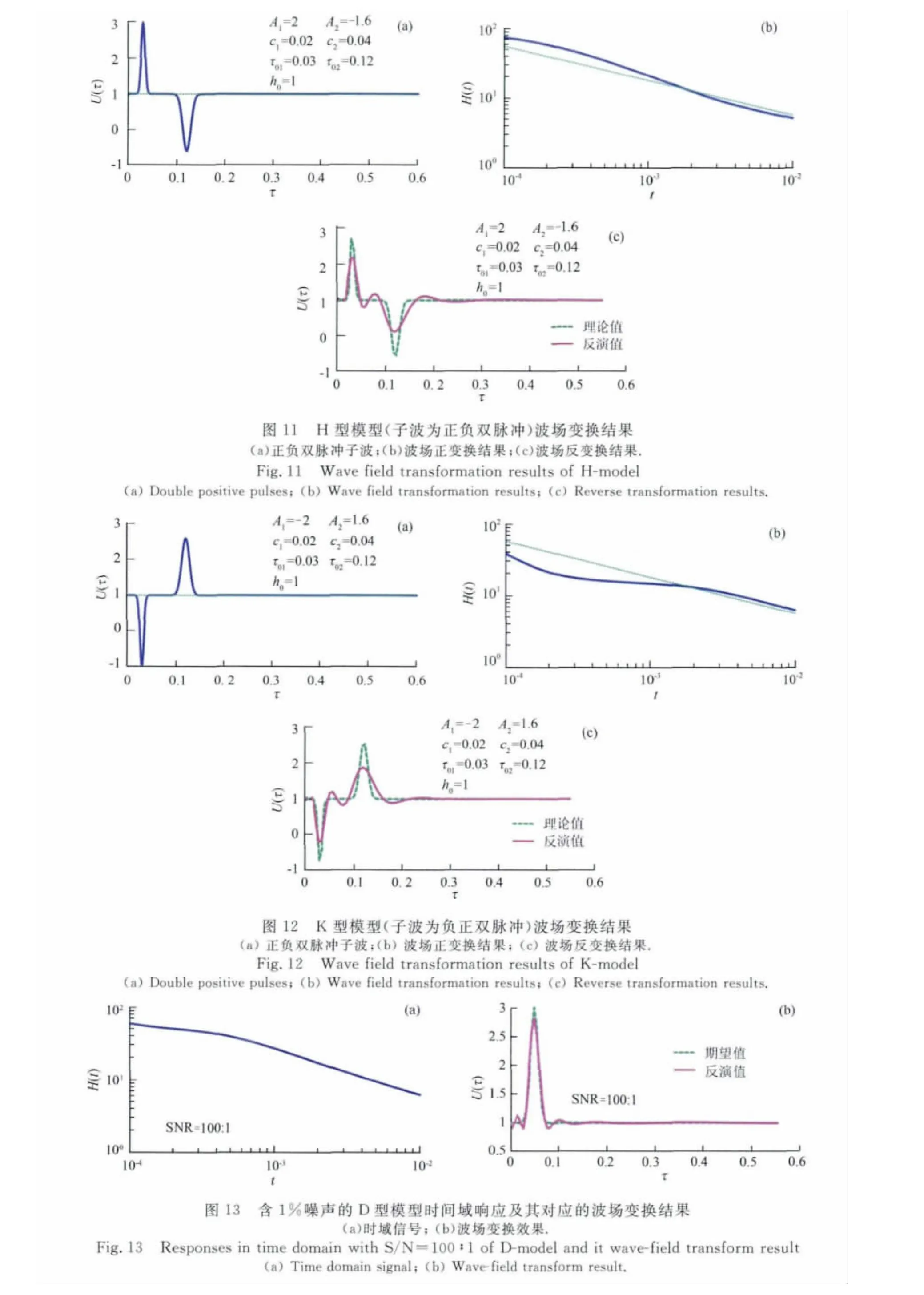

由图16b与20b可以明显看出噪声使得时间域响应曲线变得很不平滑.由波场反变换结果来看,当信噪比为小于5%时,反演值与期望值吻合得较好,当信噪比超过5%时,反演值波动剧烈,与预期结果差距较大.因此对于野外信号采集必须控制噪音为5%以下,并且对于局部不光滑数据不能直接进行处理,需要对数据进行平滑去噪后才能进行波场变换.因此本文方法完全适用于实际数据的处理.当然为提高波场变换的适用性也可以采取其他手段,如合成孔径方法来提高波场的抗噪能力.
5.3 实测数据分析
在前文中已经利用模型对方法进行了验证,现对实测数据进行处理,进一步对算法进行验证.以某煤田采空区实测数据为例进行分析.仪器选用GDP-32电法工作站,用中心回线方式进行测量,测线为1320、1360、1400,测点300—900.

测区视电阻率剖面如图21所示.由图可知,区域视电阻率变化较大,变化范围从几十到几百欧姆米,总体表现为地表黄土覆盖视电阻率高,基底视电阻率较高.在点号300—500深度120~350m左右范围内,有一低阻异常,结合工区资料,推断为富水采空区.根据视电阻率断面图可大概推断采空区分布在点号(300,500)区间,由于深层电阻率变化缓慢,不容易估计采空区底界面,从视电阻率断面图可初步估计底界面在300~400m范围内.

图21 测区视电阻率断面图(a)1320线视电阻率深度断面图;(b)1360线视电阻率深度断面图;(c)1400线视电阻率深度断面图.Fig.21 Apperant resistivity section of the survey data(a)Apperant resistivity section of line 1320;(b)Apperant resistivity section of line 1360;(c)Apperant resistivity section of line 1400.
为了验证方法效果,给出测线1320、1360、1400,点号为300到500间11个测点数据的全域波场变换结果.如图22所示,其横轴为点数,纵坐标为虚拟时间,单位为,在虚拟时间为 100处有一明显的电性分界面,在虚拟时间为 400左右也有一电性分界面分布.根据图21可知地下介质类似于三层模型,与图22波场变换结果相符.但是波场变换结果显示的界面与视电阻率界面并不一致,这是由于图22纵轴为虚拟时间,要想得到真实的地下介质起伏形态还需要进行速度分析与延拓成像,虚拟波场速度是一个与地下介质电阻率有关的量,经过波场延拓后,得到深度剖面,其显示结果应与视电阻率起伏形态相似.综上所述,本文方法正确有效,能够用于实际数据处理,并且对推断多层采空具有明显的优势.
6 结 论
文中主要研究由扩散方程到波动方程转换的数值计算方法.首先,对前人推导的波场表达式进行数值离散,分析了多种离散方式的优劣,选用效果较好的等间距剖分进行离散.然后,在前人工作基础上,采用预条件正则化共轭梯度法,实现了全时域波场反变换.正则化共轭梯度法适合病态方程的求解,采用SSOR预条件子进行预条件,将系数矩阵条件数降为原条件数的平方根,有效改善方程的病态性,这样选择较小的正则化参数就可以得到较高的精度,有利于运用正则化共轭梯度实现方程的迭代计算.
实现波场反变换后,对算法进行了验证,并对瞬变电磁虚拟波场的性质进行了详细讨论.利用均匀模型(即子波为常数时),对反变换计算方法进行验证,得到的子波与理论子波误差小于2%,说明PRCG算法是有效的.对两层(子波为单脉冲)和三层(子波为双脉冲)模型进行反变换,得到的子波与理论子波相似,由此可以证明该方法适合于复杂介质.对两层模型和三层模型进行了详细的分析,可知虚拟波场对浅层目标分辨较好,随着深度的增加,虚拟波场幅值迅速衰减,子波展宽严重,分辨率逐渐降低.

图22 测区全域波场变换结果(a)1320线全域波场变换结果;(b)1360线全域波场变换结果;(c)1400线全域波场变换结果.Fig.22 The full-time wave-field transformation of the survey data(a)The full-time wave-field transformation of line 1320;(b)The full-time wave-field transformation of line 1360;(c)The full-time wave-field transformation of line 1400.
利用文中所述方法和选择的正则化参数,在选定时段对于含有噪声的瞬变电磁信号进行波场变换,当干扰在5%以下时波场变换结果与理论值吻合较好.但是当干扰大于5%时,波场变换结果与理论值相差较大.因此瞬变电磁信号的前处理,即信号平滑与去噪是必要的.当然我们也可以增大正则化参数,但这样做势必影响波场的分辨率.
经过波场反变换后,虚拟波场不仅满足波动方程,而且与地震子波类似,具有波的传播特性.这为后续利用波动方程偏移成像方法提供了良好的基础.
(
)
[1] Levv S,Oldenburg D,Wang J.Subsurface imaging using magnetotelluric data.Geophysics,1988,53(1):104-117.
[2] 王家映.我国大地电磁测深研究新进展.地球物理学报,1997,40(S1):206-216.Wang J Y.New development of magnetotelluric sounding in China.ActaGeophysicaSinica(ChineseJ.Geophys.)(in Chinese),1997,40(S1):206-216.
[3] 王家映,Oldenburg D,Levy S.大地电磁测深的拟地震解释法.石油地球物理勘探,1985,20(1):66-79.Wang J Y,Oldenburg D,Levy S.The magnetotelluric interpretation simuiating seismic method.OilGeophysical Prospecting(in Chinese),1985,20(1):66-79.
[4] 左海燕,王家映,方胜.关于大地电磁的平均速度问题.石油物探,1986,25(1):84-97.Zuo H Y,Wang J Y,Fang S.On magnetotelluric average velocity.GeophysicalProsectingforPetroleum(in Chinese),1986,25(1):84-97.
[5] 王家映.大地电磁拟地震解释法.北京:石油工业出版社,1995.Wang J Y.Magnetotelluric Sounding Interpretation Method(in Chinese).Beijing:Petroleum Industry Press,1995.
[6] 薛国强,李貅,宋建平等.回线源瞬变电磁成像的理论分析及数值计算.地球物理学报,2004,47(2):338-343.Xue G Q,Li X,Song J P,et al.Theoretical analysis and numerical calculation of loop-source transient electromagnetic imaging.ChineseJ.Geophys.(in Chinese),2004,47(2):338-343.
[7] 郭文波.瞬变电磁拟地震解释法研究[博士论文].西安:长安大学,2000.Guo W B.Transient electromagnetic pseudo-seismic interpretation method research[Ph.D.thesis](in Chinese).Xi′an:Chang′an University,2000.
[8] 牛之琏.时间域电磁法原理.长沙:中南大学出版社,2007.Niu Z L.Principle of Time Domain Electromagnetic Method(in Chinese).Changsha:Central South University Press,2007.
[9] 薛国强,李貅,底青云.瞬变电磁法正反演问题研究进展.地球物理学进展,2008,23(4):1165-1172.Xue G Q,Li X,Di Q Y.Research progress in TEM forward modeling and inversion calculation.ProgressinGeophysics(in Chinese),2008,23(4):1165-1172.
[10] 李貅.瞬变电磁测深的理论与应用.西安:陕西科学技术出版社,2002.Li X.Transient Electromagnetic Sounding Theory and Application (in Chinese).Xi′an.Shaanxi Science and Technology Press,2002.
[11] Zhdanov M S,Dmitriev V I,Fang S,et al.Quasi-analytical approximations and series in electromagnetic modeling.Geophysics,2000,65(6):1746-1757.
[12] Zhdanov M S,Portniaguine O.Time-domain electromagnetic migration in the solution of inverse problems.Geophysics,1997,131(2):293-309.
[13] Zhdanov M S,Traynint P,Booker J R.Underground imaging by frequency-domain electromagnetic migration.Geophysics,1996,61(3):666-682.
[14] Lavrent′ev M M,Rornanov V G,Shishatskii S P.Ill-posed problems of mathematical physics and analysis(in Russian).Providence RI:American Mathematical Society,1986.
[15] 陈本池,李金铭,周凤桐.瞬变电磁场拟波动方程偏移成像.石油地球物理勘探,1999,34(5):546-554.Chen B C,Li J M,Zhou F T.Quasi wave equation migration of transient electromagnetic field.OGP(in Chinese),1999,34(5):546-554.
[16] 陈本池,周凤桐,李金铭.瞬变电磁场的波场变换研究.物探与化探,1999,23(3):195-201.Chen B C,Zhou F T,Li J M.The wavefield transformation study of transient electromagnetic field.GeophysicalandGeochemicalExploration(in Chinese),1999,23(3):195-201.
[17] 郭文波,李貅,薛国强等.瞬变电磁快速成像解释系统研究.地球物理学报,2005,48(6):187-192.Guo W B,Li X,Xue G Q,et al.A study of the interpretation system for TEM tomography.ChineseJ.Geophys.(in Chinese),2005,48(6):187-192.
[18] 李貅.瞬变电磁虚拟波场的三维曲面延拓成像研究[博士论文].西安:西安交通大学,2005.Li X. The study about 3-D surface extension imaging technique in transient electromagnetic fictitious wave-field[Ph.D.thesis] (in Chinese).Xi′an:Xi′an Jiaotong University,2005.
[19] 李貅,郭文波,胡建平.瞬变电磁测深快速拟地震解释方法及应用效果.西安工程学院学报,2001,23(3):42-45.LI X,Guo W B,Hu J P.The method and application effects of pseudo-seismic interpretation of TEM.JournalofXi′an EngineeringUniversity(in Chinese),2001,23(3):42-45.
[20] 李貅,戚志鹏,薛国强等.瞬变电磁虚拟波场的三维曲面延拓成像.地球物理学报,2010,53(12):3005-3011.Li X,Qi Z P,Xue G Q,et al.Three dimensional curved surface continuation image based on tem pseudo wave-field.ChineseJ.Geophys.(in Chinese),2010,53(12):3005-3011.
[21] 李貅,薛国强,宋建平等.从瞬变电磁场到波场的优化算法.地球物理学报,2005,48(5):1185-1190.Li X,Xue G Q,Song J P,et al.An optimize method for transient electromagnetic field-wave field conversion.Chinese J.Geophys.(in Chinese),2005,48(5):1185-1190.
[22] 朱宏伟,李貅,张军等.瞬变电磁法三维拟地震成像信息提取技术.地球物理学进展,2010,25(5):1648-1656.Zhu H W,Li X,Zhang J,et al.Information collecting technology in 3-D pseudo-seismic imaging of transient electromagnetics.ProgressinGeophysics(in Chinese),2010,25(5):1648-1656.
[23] 刘银爱.合成孔径瞬变电磁偏移成像技术研究[博士论文].西安:长安大学地球探测与信息技术,2010.Liu Y A.A research on TEM imaging method based on synthetic-aperture technology [Ph.D.thesis](in Chinese).Xi′an:Chang′an University,2010.
[24] Xue G Q,Yan Y J,Li X.Control of the waveform dispersion effect and applications in a TEM imaging technique for identifying underground objects.JournalofGeophysicsand Engineering,2011,8(2):195-201,doi:10.1088/1742-2132/8/2/007.
[25] 刘继军.不适定问题的正则化方法及应用.北京:科学出版社,2005.Liu J J. Regularization Methods and Applications (in Chinese).Beijing:Science Press,2005
[26] 王彦飞.反演问题的计算方法及其应用.北京:高等教育出版社,2007.Wang Y F.Computational Methods for Inverse Problems and Their Applications(in Chinese).Beijing:Higher Education Press,2007.
[27] 王彦飞,斯捷潘诺娃I E,提塔连科V N等.地球物理数值反演问题.北京:高等教育出版社,2011.Wang Y F,Stefan Nova I E,Titalianke V N,et al.Inverse Problems in Geophysics and Solution Methods(in Chinese).Beijing:Advanced Education Press,2011.
[28] 沈梅芳.瞬变电磁的虚拟波场偏移成像研究[博士论文].西安:长安大学,2006.Shen M F.The fictitious wavefield migration imaging of transient electromagnetic method[Ph.D.thesis](in Chinese).Xi′an:Chang′an University,2006.
[29] Kunetz G.Processing and interpretation of Magnetotelluric soundings.Geophysics,1972,37(6):1005-1021.
[30] Lee K H,Liu G,Morrison H F.A new approach to modeling the electromagnetic response of conductive media.Geophysics,1989,54(9):1180-1192.
[31] Lee S,McMechan G A,Aiken C L V.Phase-field imaging:The electromagnetic equivalent of seismic migration.Geophysics,1987,52(5):678-693.
[32] Bai Z,Zhang S.A regularized conjugate gradient method for symmetric positive definite system of linear equations.JournalofComputationalMathematics,2002,20(4):437-448.
[33] 周翠荣.改进的正则化共轭梯度法[博士论文].杭州:电子科技大学,2010.Zhou C R.The improved regularized conjugate gradient method(in Chinese)[Ph.D.thesis].Hangzhou:University of Electronic Science and Technology,2010.
[34] 何小祥,刘梅林.SSOR预处理技术在二维电磁特性TDFEM分析中的应用.南京航空航天大学学报,2006,38(6):670-673.He X X,Liu M L.Application of SSOR preconditioning technique in TDFEM for 2-D electromagnetic analysis.JournalofNanjingUniversityofAeronautics&Astronautics(in Chinese),2006,38(6):670-673.
[35] 韦志辉,周荣富.SSOR方法的数值稳定性.东南大学学报(自然科学版),1990,20(3):108-113.Wei Z H,Zhou F R.Numerical stability of SSOR method.JournalofSoutheastUniversity(in Chinese),1990,20(3):108-113.
[36] 胡家赣.线性代数方程组的迭代解法.北京:科学出版社,1991.Hu J G.Linear Algebraic Equations Iterative Method (in Chinese).Beijing:Science Press,1991.
[37] 赵俊华.改进的SAOR预条件共轭梯度法[博士论文].太原:太原理工大学,2005.Zhao J H.Modified SAOR preconditioned conjugate Gradient method [Ph.D.thesis](in Chinese).Taiyuan:Taiyuan University of Technology,2005.
[38] Zhdanov M S,Ellisz R,Mukherjee S.Three-dimensional regularized focusing inversion of gravity gradient tensor component data.Geophysics,2004,69(4):925-937.
[39] Zhdanov M S,Tolstaya E.A novel approach to the model appraisal and resolution analysis of regularized geophysical inversion.Geophysics,2006,71(6):R79-R90.
[40] Wang Y F.A restarted conjugate gradient method for illposed problems.ActaMathematicaeApplicataeSinica(EnglishSeries),2003,19(1):31-40.
[41] 陈晓斌,赵国泽,汤吉等.大地电磁自适应正则化反演算法.地球物理学报,2005,48(4):937-946.Chen X B,Zhao G Z,Tang J,et al.An adaptive regularized inversion algorithm for magnetotelluric data.ChineseJ.Geophys.(in Chinese),2005,48(4):937-946.
[42] Tong X Z,Liu J X,Xu L H.Damped gauss-newton optimization algorithm for tow-dimensional magnetotelluric regularization inversion.ICIEC,2009,12
[43] 刘小军,王家林,吴健生.二维大地电磁正则化共轭梯度法反演算法.上海地质,2007,(1):71-74.Liu X J,Wang J L,Wu J S.Inversion algorithm of 2-D magnetotelluric data using regularized conjugate gradient method.ShanghaiGeological(in Chinese),2007,(1):71-74.
[44] 戴亦军,童孝忠,张连伟等.利用一维正则化反演进行大地电磁测深数据拟二维反演解释.物化探计算技术,2012,34(1):33-38.Dai Y J,Tong X Z,Zhang L W,et al.Pseudo-2Dinversion interpretation for magnetotelluric data using 1Dregularization inversion method.ComputingTechniquesforGeophysical andGeochemicalExploration(in Chinese),2012,34(1):33-38.
[45] 张军,李貅,赵莹等.瞬变电磁虚拟波场高分辨成像技术研究.地球物理学进展,2011,26(3):1077-1084.Zhang J,Li X,Zhao Y,et al.A technology research of highresolation imaging for the transient electromagnetic pseudo wave field.ProgressinGeophysics(in Chinese),2011,26(3):1077-1084.
