双足机器人跟踪误差在线修正方法

张世龙，刘国栋

(江南大学物联网工程学院，江苏 无锡 214122)

1 概述

双足机器人是一门由仿生学、机械设计、加工和计算机控制理论以及人工智能等多种学科形成的交叉学科。然而，步态规划是研究双足机器人控制的难点和热点，步行过程必须保证双足机器人的稳定性[1]。双足机器人控制多采用静态步态规划得到一步或多步参考轨迹，由关节控制器伺服跟踪期望轨迹。但由于机器人自身的机械误差，模型误差以及地面摩擦力等环境因素的影响，机器人的实际步态必然与期望步态之间会产生一定的误差，这些误差的积累很可能会使机器人不稳定而摔倒[2]。为了减小或消除这些误差，必须对机器人的步行模式进行在线修正，以实现机器人的稳定行走。

为解决此问题，学者们曾提出过对机器人进行在线全身关节实时修正的方法，但由于机器人在行走时会存在惯性力的作用，在进行不适当的实时修正时，会导致机器人的零力矩点(Zero Moment Point, ZMP)位置波动，出现不稳定现象，从而导致使机器人的步行速度受到限制[3]。

本文提出一种双足机器人跟踪误差在线修正方法。利用双足机器人传感器反馈，实时检测机器人质心(Centre of Mass, COM)的偏差与零力矩点的偏差，根据偏差计算得出步态修正时间点与修正量，在线修正双足机器人实际状态与目标状态的偏差。

2 双足机器人模型及步行模式的生成

2.1 双足机器人模型

通过分析机器人的运动特性可知，机器人脚杆的运动速度快于质心的运动速度，并大幅变化。因此，从能量角度来看机器人的质量应该尽量集中于上半身。另外，在行走的过程中，转动集中于质量较小的下半身，行走时转动能量要比平动能量小很多，转动能量可以忽略不计。因此，可以将机器人所有连杆的质量集中到机器人上半身的质心上，只考虑质心质量，并忽略各脚杆的转动惯量[4]。三维线性倒立摆简化模型如图1所示。

图1可以使用ZMP的定义描述如下：

通常情况下机器人的质心高度保持不变，即约束面水平(kx=ky= 0)。

将式(2)代入式(1)得到如下与 Z轴运动相独立的运动方程[6]：

由式(3)可知，根据机器人的ZMP点，可以求得机器人的质心运动。

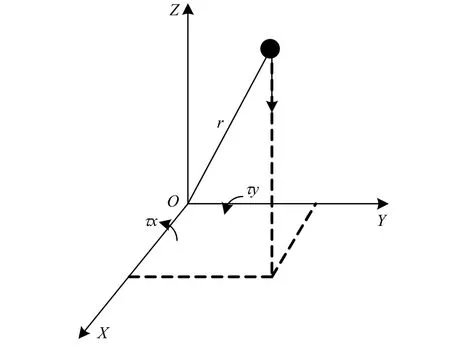
图1 三维线性倒立摆简化模型

2.2 步行模式的生成

在给定机器人的步行参数(步长、步宽、步行周期)、起点和终点的情况下，可以规划出机器人的 ZMP轨迹，如图2所示。

图2 机器人的ZMP规划轨迹

由式(3)可以得到机器人的质心轨迹，如图3所示。

图3 机器人的质心轨迹

基于ZMP步行模式生成的方法为：由机器人的多连杆模型求得机器人的质心位置，机器人的质心高度 zc保持不变，质心在XOY平面上的轨迹可由图3得到，机器人足部轨迹可由图2的ZMP轨迹得到[7]。一旦机器人质心和足部轨迹确定，则可以根据机器人的逆运动学得到腿部各关节的角度，从而由电机驱动机器人运动。

3 基于SSP和DSP的机器人在线修正

大多数双足机器人研究都将步行过程视为由连续单腿支撑相和瞬态双足支撑相组成的周期运动，然而，在人类步行运动中，DSP约占整个步态周期的0.15%～0.25%，仅把 DSP作为瞬态过程考虑是不合理的[8]。同时，由于双足机器人在行走过程中，要保持不倾倒就必须使得机器人的ZMP点在稳定区域内[9]。机器人的稳定支撑区域如图 4所示。

图4 机器人的稳定支撑区域

在图4中，SSP阶段稳定区域为支撑脚；DSP阶段稳定区域为两脚之间的部分和支撑脚。从图 4可以看出，单腿支撑阶段ZMP的稳定区域相对于双腿支撑阶段ZMP的稳定区域比较小，即ZMP的稳定裕度不同[10]。这就导致了SSP和DSP的稳定性不同。

从模仿人类的角度出发，由于DSP和SSP的稳定性差异很大，因此应将在线实时修正分为SSP和DSP进行考虑。在SSP阶段，通过引入误差裕量函数得到在线修正的时间点；在DSP阶段，通过设置误差限值寻找修正时间点。在机器人实际行走的过程中，通过SSP阶段修正方法可以补偿DSP阶段的不足，DSP阶段也可以补偿SSP阶段的不足，通过 2种方法的相互配合，从而达到提高机器人稳定性和步行速度的目的。

3.1 单腿支撑阶段的在线全身关节修正

在双足机器人步行过程中，单腿支撑阶段在步行周期中所占的比例是非常大的，而且三维线性倒立摆模型主要针对单腿支撑阶段进行了分析[11]。由此可以看出SSP在机器人行走过程中的重要性。

根据步行模式的生成原理，质心的轨迹可以由ZMP轨迹根据三维倒立摆模型求得。但此时的质心轨迹是离线规划好的，而实际的质心轨迹由于外部环境的影响一定会与期望的质心轨迹有偏差。此时，如果不进行质心位置修正，势必会影响ZMP的位置，从而导致机器人行走不稳定。然而，机器人在单腿支撑阶段的稳定裕度是比较小的，如果对机器人的质心进行实时修正，由于修正过程中需要对机器人全身关节进行补偿，这会引起ZMP位置的波动，进而导致机器人处于不稳定状态。为了解决此问题，本文提出了一种设置误差裕量函数的方法。函数如下：

其中，坐标向量ZMPact是实际得到的ZMP位置；坐标向量ZMPref是离线规划的ZMP位置；EerZMP为ZMP位置误差向量；|·|符号表示对相应的向量的各分量取绝对值；而参数K需根据实际环境确定。

通过此函数与质心误差函数进行比较。质心误差函数如下：

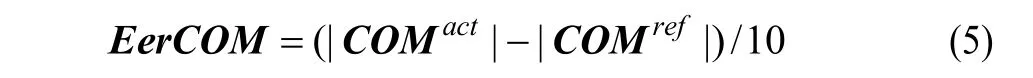
其中，COMact是实际检测并计算的质心位置向量；COMref是离线规划的质心位置向量；EerCOM 为质心位置误差向量。

在进行质心位置修正时，通过检测ZMP与COM的实际位置计算出EerZMP与EerCOM的值。其中，||·||符号表示对相应变量取模。

当||EerCOM||＜||EerZMP||时，此时可以认为实际质心轨迹能够跟踪期望的质心轨迹，即机器人是稳定的，不需要对质心位置进行在线修正。

当||EerCOM||≥||EerZMP||时，此时实际质心轨迹已严重偏离期望的质心轨迹，即机器人处于不稳定状态，需要对质心位置进行在线修正。

通过此方法可以解决在单腿支撑阶段质心实时修正与ZMP位置波动之间的冲突，即质心的跟踪误差是有一定裕量的，并且裕量的大小是根据实时检测到 ZMP的值来确定的。

经转染PRKCI表达载体的SCC-15细胞，与对照组相比，PRKCI基因的表达量显著增加且明显高于未转染PRKCI表达载体的对照组细胞(图2A，2B)。

关节修正的数值解法如下[12]：

(1)给定期望的质心位置和ZMP位置。

(2)检测并计算实际的质心位置和ZMP位置。

(3)计算质心位置误差 EerCOM 和 ZMP位置误差EerZMP。

(4)当||EerCOM||≥||EerZMP||时，执行步骤(5)，当||EerCOM||＜||EerZMP||时，返回步骤(1)。

(5)计算关节角的修正向量δq。

为了实现上述算法的步骤(5)，需要计算出修正向量δq以便减少机器人质心位置的误差。假设从当前状态的关节角向量q减去一个δq，考虑质心位置的微小变化向量δp，δp=Fp(δ q )，当δq很小时，可以通过雅克比矩阵描述和计算，改写成：

其中，J为雅克比矩阵，它取决于机器人当前的位姿，一旦式(6)确定之后，由于δP可由下式求得：

3.2 双腿支撑阶段的在线全身关节修正

相对于单腿支撑阶段，双腿支撑阶段的稳定性好很多。因此，在对双腿支撑阶段进行质心修正时，可以不必考虑质心实时修正与ZMP位置波动间的冲突问题。

本文对质心位置进行实时修正，即全身关节在线补偿。但是，在实际环境中。实际的质心轨迹完全跟踪期望的质心轨迹，而达到零误差是不可能的。因此，在此阶段，设置误差限值EM，可以根据实际环境确定。当||EerCOM||≥EM时，继续进行质心在线修正；当||EerCOM||＜EM时，实际的质心能够跟踪期望的质心。

关节修正数值解法如下：

(1)给定期望的质心位置和ZMP位置。

(2)检测并计算实际的质心位置和ZMP位置。

(3)计算质心位置误差EerCOM。

(4)当||EerCOM||≥EM 时，执行步骤(5)，当||EerCOM||＜EM时，返回步骤(1)。

(5)计算关节角的修正向量δq。

4 实验结果与分析

本文实验的目的在于验证双足机器人步行模式分阶段处理的控制性能，完成完整步行周期的实验。首先，利用Matlab平台建立机器人模型。通过仿真得到了基于三维线性倒立摆模型的机器人步行轨迹，如图 5所示。机器人的步行参数为：步长0.1 m，步宽0.1 m，步行周期为0.92 s。

图5 基于三维倒立摆模型的机器人步行轨迹

将本文方法应用于实体机器人，通过 AFU-10进行试验，图6显示了实际步行过程中期望的ZMP轨迹和实际检测到的 ZMP轨迹对比，此过程中没有采用本文方法。从图 6可以看出，机器人的跟踪误差比较大，一旦出现外界干扰就很容易跌倒，并且步行周期已达到所能承受的最小值。

图7为采用本文方法后得到的ZMP轨迹和质心轨迹。设定EM=0.0108，参数K=0.01。可以看出，采用本文方法后机器人的稳定性明显提高，步行周期由1.3 s左右提高到了0.92 s，从而步行速度上限提高了25%左右。并且双足机器人步行时对外部环境具有了一定的抗干扰能力。

图6 未使用本文方法的ZMP轨迹和质心轨迹

图7 使用本文方法的ZMP轨迹和质心轨迹

将本文方法应用于RoboCup(3D)项目比赛，结果如图8所示。应用本文方法后，双足机器人行走起来更加稳定，行走速度明显提高，并且在比赛中荣获一等奖的好成绩。

图8 RoboCup项目实验结果

5 结束语

双足机器人的步行稳定性一直是机器人研究的热点及难点。本文提出一种双足机器人跟踪误差在线修正方法。解决了机器人在线修正过程中质心实时修正与ZMP位置波动之间的冲突问题。实验结果表明了该方法有效性。但该方法仅局限于在特定环境下的稳定行走，将其应用于机器人在其他环境下的稳定行走是下一步的研究方向。

[1]Morimoto J, Endo G, Nakanishi J, etal.A Biologically Inspired Biped Locomotion Strategy for Humanoid Robots:Modulation of Sinusoidal Patterns by a Coupled Oscillator Model[J].IEEE Transactions on Robotics, 2008, 24(1):185-191.

[2]刘 飞, 陈小平.使用零力矩点轨迹规划的四足机器人步态进化方法[J].机器人, 2010, 32(3): 398-404.

[3]Park J H, Kim E S.Foot and Body Control of Robots to Walk on Irregularly Protruded Uneven Surfaces[J].IEEE Transactions on Systems, Man, and Cybernetics, 2009, 39(1): 289-297.

[4]Liu Hsin-Yu, Wang Wen-June, Wang Rong-Jyue.A Course in Simulation and Demonstration of Humanoid Robot Motion[J].IEEE Transactions on Education, 2011, 54(2): 255-262.

[5]Shimmyo S, Tomoya S, Ohnishi K.Biped Walking Pattern Generation by Using Preview Control with Virtual Plane Method[C]//Proc.of the 11th IEEE International Workshop on Advanced Motion Control.Nagaoka, Japan: IEEE Conference Publications, 2010.

[6]Shimmyo S, Ohnishi K.Nested Preview Control by Utilizing Virtual Plane for Biped Walking Pattern Generation Including COG Up-down Motion[C]//Proc.of the 36th Annual Conference on IEEE Industrial Electronics Society.Glendale,USA: IEEE Conference Publications, 2010.

[7]梶田秀司.仿人机器人[M].管贻生, 译.北京: 清华大学出版社, 2007.

[8]朱志斌, 王 岩, 陈兴林.一种双足机器人实时步态规划方法及相关数值算法[J].机器人, 2008, 30(6): 521-527.

[9]伊 强, 陈 恳, 刘 莉, 等.考虑综合步行约束的仿人机器人参数化3D步态规划方法[J].机器人, 2009, 31(4): 342-350.

[10]Jimmny O.A Hybrid CPG-ZMP Controller for the Real-time Balance of a Simulated Flexible Spine Humanoid Robot[J].IEEE Transactions on Systems, Man, and Cybernetics, 2009,39(5): 547-561.

[11]汤 卿, 熊 蓉, 褚 健.给予最优化线性搜索的稳定步态规划方法[J].控制理论与应用, 2008, 25(4): 661-664.

[12]黄元林, 付成龙, 王健美, 等.双足跑步机器人控制方法研究概述[J].机器人, 2009, 31(4): 370-377.

[13]敬成林, 李祖枢, 薛方正.双足机器人逆运动学的模糊自适应算法[J].机器人, 2010, 32(4): 534-539.