电力数据中的幂律分布特性
2013-09-29王冠男邓春宇郑亚芹
王冠男,邓春宇,赵 悦,郑亚芹
(北京国电通网络技术有限公司大数据业务部 北京 100070)
1 引言
在自然界和社会生活中,经常存在这样的数据,数值在某个特征附近变化,并且变化较小,这一类数据被称为正态分布,具有很多优秀的特性,如图1(a)所示。比如人的身高、学生的考试成绩、同质群体的红细胞数以及数理统计中随机误差等都符合正态分布。在传统数据挖掘方法中,正态分布被誉为概率论里最重要的分布。
然而,随着大数据时代的到来,人们有能力处理完全数据而不是样本数据,因此,现实中很多完全数据不再符合正态分布,比如个人收入的分布、变化尺度的范围很宽,波动可以跨越很多数量级。根据这类数据可以画出一条向右偏斜并且拖着长尾巴的累积分布曲线,显然,它与正态分布曲线有显著的不同,如图1(b)所示。这种长尾分布表明,绝大多数个体的值很小,只有少数个体的值相当大。这种现象被称为长尾效应,或者重尾法则,本文研究的幂律分布是长尾分布中重要的一种[3,4]。
研究表明,90%的电力指标数据都不符合正态分布。确定数据是否为正态分布在数据的探索性分析中具有举足轻重的作用,因为正态分布是很多统计方法和数据挖掘方法所必需的条件,比如线性和非线性回归模型、因子分析、典型相关分析以及主成分分析等,甚至包括最基本的线性相关性系数的计算。若数据不符合正态分布,需要采取其他相应的办法,如数据转换或者更换分析方法,否则轻者导致模型计算结果的不准确性,严重者更会影响针对算法结果所做的决策。本文主要针对电力数据中的指标进行分析,研究其真正的分布规律,主要从3个方面展开,首先介绍数据源和相关指标,然后阐述电力指标数据的幂律分布特性以及细分行业用电量的对数正态分布特性,最后结合业务背景解释电力指标符合幂律分布的原因。
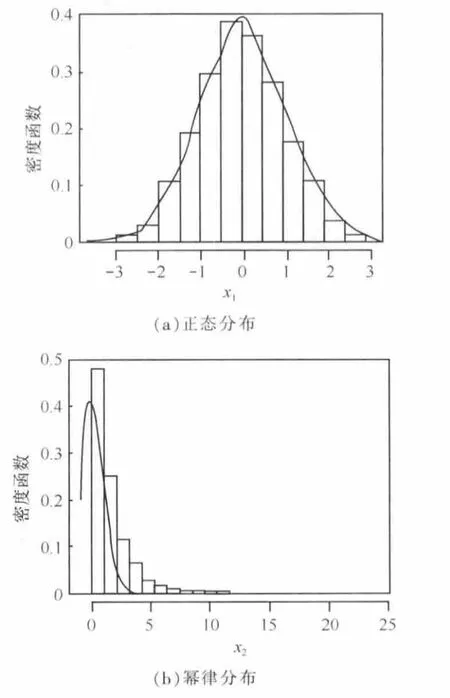
图1 正态分布和幂律分布
2 数据描述
2.1 数据源
本文选择全国发电量、国家电网公司售电量以及全社会用电量3个指标作为分析研究的目标,选择原因如下。
·全社会用电量与国家经济密切相关,研究表明,用电量的增长影响GDP的增长,而GDP的增长对用电量的增长影响不大,即用电量增长和GDP增长的关系是从用电量到GDP增长的单向因果关系。
·全国发电量是直接衡量一个国家经济状况的重要指标。国家电网公司是关系国家能源安全和国民经济命脉的重要骨干企业,公司的售电量能够反映公司甚至国家的供电能力。3个电力指标具有较强的相关性。
表1阐述了所选3个电力指标的维度、时间和区域。本文所选取的时间为2011-2013年每年的2月和7月。
2.2 电力指标的非正态分布特性
本文采取密度函数曲线检验法和夏皮罗·威尔克提出的W统计量,将数据和图形相结合,共同验证全社会发电量、国家电网售电量和全国用电量的非正态分布特性。
图2展示了3个指标的密度函数曲线,由于空间限制,时间维度是2012年2月、2012年7月、2013年2月、2013年7月。由图2可知,3个电力指标大多集中在较小的数值上,只有少数分布在较大的数值上,在空间维度上不符合正态分布,并且都具有长尾分布的特征。
表2~表4分别展现了2008-2013年所有2月份和7月份中3个指标的W统计量检验结果,即P值。
由表2~表4可知,全国发电量、国家电网公司售电量和全社会用电量的W统计检验的结果都小于0.05,即有不到5%的信心认为3个电力指标符合正态分布,下文将进一步分析3个指标分别符合何种分布。
3 电力指标的幂律分布特征
3.1 幂律分布特征
长尾和幂律的区别是:幂律分布需要数据必须在统计意义上可以被幂律曲线拟合,而对于长尾分布而言,能否被幂律曲线精确地拟合并不重要,重要的是有一个长长的尾巴。已知全国用电量、国家电网公司售电量和全社会发电量属于长尾分布,但是仍需要进一步证明其为幂律分布。

表1 全国发电量、国家电网公司售电量、全社会用电量的数据描述
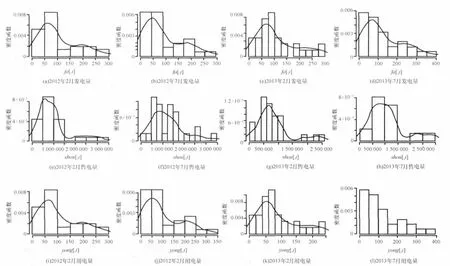
图2 全国发电量、国家电网售电量和全社会用电量3个指标的密度函数曲线

表2 全国发电量的正态分布W统计量检验结果

表3 国家电网公司售电量的正态分布W统计量检验结果

表4 全社会用电量的正态分布W统计量检验结果
幂律分布的分布特征如图1(b)所示,通用计算式为y=cx-r,x和 y是正的随机变量,c、r为常数,且大于 0。幂律分布的特点是绝大多数事件的值很小,只有少数事件的值相当大。将幂律分布公式的两边分别取对数,则ln x与ln y存在以下的线性关系:1n y=1n c-r1n x,幂律分布在双对数坐标下表现为一条斜率为幂指数的负数的直线,这一线性关系是判断某个随机变量是否满足幂律的依据,r为幂律指数。
图3展示了3个电力指标的幂律分布特征,时间维度是2012-2013年每年的2月份和7月份。由图3可知,除了特殊原因引起的较小数值外(西藏地区),其他数值基本符合线性关系,并且幂律指数为正数,因此3个指标符合幂律分布的特征,属于幂律分布。
表5~表7分别展示了3个电力指标在双对数坐标下的参数拟合结果,其中,幂律指标r都大于-2,验证了图3的结论,全国发电量、国家电网公司售电量和全社会用电量符合幂律分布。
3.2 用电量的对数正态分布特征

图3 全国发电量、国家电网公司售电量和全社会用电量的幂律分布特征

表5 全国发电量的幂律分布检验结果

表6 国家电网公司售电量的幂律分布检验结果

表7 全社会用电量的幂律分布检验结果
由上文可知,全国发电量、国家电网公司售电量和全国用电量符合幂律分布的特性,与其他两个指标相比,用电量具有特殊的优良特性。
已知两个变量X和Y无论独立与否,X+Y的和仍然服从正态分布。若X和Y服从对数正态分布,则仍然服从对数正态分布,而X+Y却不符合这一规律。通过分析,本文发现大部分细分行业的用电量服从对数正态分布,而细分行业用电量之和却不符合这一规律,比如全国用电量、第一产业用电量、第二产业用电量、第三产业用电量等。在第4节中,将详细阐述细分行业用电量服从对数正态分布的根本原因。
本文选择具有代表性的5个细分行业进行详细分析,分别是农业、轻工业、重工业、信息传输业、房地产、计算服务业。图4展示了5个行业用电量的经验累积分布函数(ECDF),应用极大似然估计的方法对分布参数进行拟合,并且将用电量与5个幂律分布进行对比,分别是指数分布、对数正态分布、逆高斯分布、帕累托分布和列维分布。由图可知,对数正态分布是最合理的拟合分布。
对数正态分布的概率密度函数为:

其中:
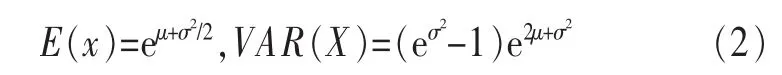
对数正态分布具有优秀的特性,当随机变量log X符合正态分布时,则X符合对数正态分布。即对用电量进行对数转换,就可以得到正态分布的数据,因此证明用电量符合对数正态分布不仅大大减少了数据分析的工作量,还解决了用电量不是正态分布的难题。表8展示了对数转换后细分行业用电量的正态分布检验结果。
由表8可知,所有W统计量的检验结果大于0.05,即有95%的信心认为,细分行业的用电量经过对数转换后服从正态分布,可以直接应用以正态分布为必要条件的数据分析和挖掘方法。
4 原因分析
由上文已知,全国发电量、国家电网公司售电量和全国用电量符合幂律分布的特性,并且细分行业的用电量服从对数正态分布,本节主要结合业务背景阐述3个电力指标符合幂律分布以及细分行业用电量服从对数正态分布的根本原因。
3个电力指标符合幂律分布特性的主要原因如下。
·由于政策、地理位置和自然环境等原因,全国经济发展严重不平衡,东部沿海地区较发达,西部等地区经济较为落后。电力和经济密不可分,是强正相关的关系,某地区的用电情况可以反映此地的经济状况,因此电力指标数据在地域上也存在不平衡的现象。

图4 细分行业用电量的ECDF
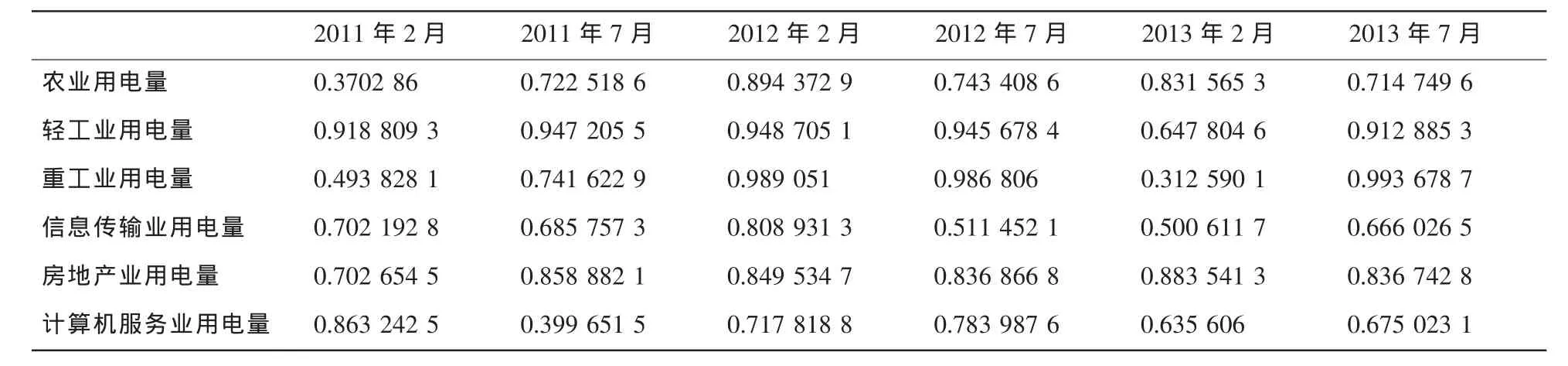
表8 细分行业用电量对数转换后的正态分布W统计量检验结果
·自然资源分布不平衡。全国的煤炭资源和水源分布不平衡,只有少数地区具有丰富的煤炭资源和水资源,这导致电力指标数据的曲线向左倾斜,并且具有幂律分布的特征。
因为电力指标数据在地域上分布不平衡,所以随着电力指标数值的增加,P(Q>q)逐渐降低,并且降低速度减缓,呈现幂函数的规律,这正是幂律分布的特征。
细分行业用电量服从对数正态分布,下面运用数学理论阐述产生此种现象的根本原因。
正态分布的变量和对数正态分布的变量存在着区别和联系,就共同点来说,两种变量都是独立变量,即用户每天的用电量是独立的,符合正态分布。两种分布最大的区别在于“加”和“乘”,这种细微的不同使得数据的分布规律也具有明显差异。
首先以布朗运动为例来解释正态分布。假设某个行业在某一天的用电量为Q1,在下一天的用电量为Q2,在单位时间Δt内,行业用电量的差值为ΔQ,增加或者减少。令Qn为n天以后某行业的累积用电量,则:
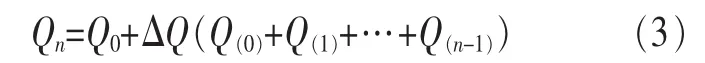
其中:

Q(i)相互独立,且 P=1)=P=-1)=1/2。Xn服从二项分布,参数为n和p=0.5,由中心极限定理可知,当n→+∞时,Qn近似服从正态分布。
但是在现实中,由于温度变化、某个月的假期时间长短的变化以及政策变化等原因,行业用电量的增减不是随机的,比如通过分析发现在2月和7月,细分行业的用电量更倾向于增加而不是减少,除非发生特殊情况。假设在单位时间Δt内,行业用电量以相同的概率增加ΔQ1,减少ΔQ2,ΔQ1和 ΔQ2为已知常数,并且 ΔQ1>ΔQ2(在某些月份ΔQ1<ΔQ2,不影响最终结果)。
求解如下方程:

得到ΔQm=ΔQ1/ΔQ2。则n天以后,行业的累积用电量为:
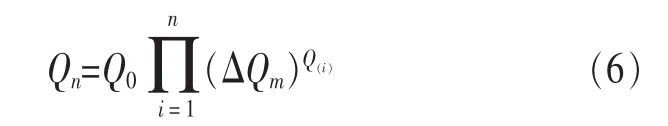
其中,Q(i)的含义保持不变,且 P(Q(i)=1)=P(Q(i)=-1)=1/2,Q(i)相互独立,即行业在某一天用电时不会考虑下一天的用电情况。正如布朗运动中的分析,Qn仍然服从二项分布。由于 ΔQ1>ΔQ2(或者 ΔQ1<ΔQ2),则分布曲线必定会向左偏。当n→+∞时,Qn近似服从对数正态分布。这符合中心极限定理的多重乘法的规则,即多个独立同分布变量的乘积符合对数正态分布。因此,在同一时间段内(本文选取一个月),各个省的细分行业用电量服从对数正态分布,且如果将细分行业继续划分,仍然服从对数正态分布。
5 结束语
本文主要针对电力指标的分布性规律进行分析研究。经过统计分析研究发现,90%以上的电力指标不符合正态分布。经验证,全国发电量、国家电网公司售电量和全社会用电量3个电力核心指标具有幂律分布的特性,其中细分行业的用电量符合对数正态分布,并且具体阐述了产生这种现象的业务原因和数学原因。
本文对电力指标的分布规律进行了深入研究,为电力大数据的探索性分析做出了贡献,并且为数据分析和挖掘方法的选择提供了理论支撑。所得的研究成果能够为电力数据分析同行提供更多的创新思路,方法和技术也可以应用到其他电力方面的数据,不仅丰富了电力数据分析领域的技术,对很多业务问题也具有理论指导意义。不符合正态分布的电力指标数据看似毫无规律,幂律分布以简洁优雅的形式,将毫不相干的事物联系在了一起。以后也将是电力数据分析中研究的热点,未来也将对电力行业中幂律分布的产生机制进行深入研究。
1 Rhee I,Shin M,Hong S,et al.On the levy walk nature of human mobility.Networking,IEEE/ACM Transactions on,2011(3)
2 Yang B,Duan W Q,Chen Z.New method to estimate scaling of power-law degree distribution and hierarchical networks.Applied Mathematics and Mechanics,2006,27(11):1475~1479
3 葛玉伟,周战,陈万田.洪泽地区配电网故障幂律分布特性.现代电子技术,2011,34(6):172~174
4 Chris A.The Long Tail.CITIC Publishing House,2005
