基于SVM的WSN运动目标位置跟踪预测方法研究

谌友仁 ，廖 兵

（1.南昌航空大学 信息工程学院，江西 南昌 330063；2.南昌航空大学 经济管理学院，江西 南昌 330063）

无线传感器网络（WSN）作为一种全新的信息获取和处理技术，在目标跟踪、入侵监测及一些定位相关领域有广泛的应用前景。其中，目标跟踪预测是无线传感器网络目标跟踪关键技术之一[1]。目前，WSN目标跟踪预测方法主要包括运动学预测方法、滤波预测方法（扩展卡尔曼滤波、粒子滤波等）、模糊理论回归预测方法和置信区域预测方法[2-3]。

近年来，随着支持向量机（SVM）技术[4-5]在各个方面的广泛应用，已有学者将支持向量机技术应用于无线传感器网络中[6-8]。支持向量机是一类基于统计学理论的新型机器学习方法，是一种基于结构风险最小化准则的学习方法，在解决小样本、非线性及高维模式识别问题中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中[9]。为了研究简单，假设本文所有部署节点位置已知，运动目标节点与部署节点是同构的。提出了一种基于支持向量回归的运动目标位置预测方法，汇聚节点收集已知节点位置信息和目标节点网络连通信息作为依据训练样本，对支持向量机中核函数和损失函数进行参数优化，使用支持向量技术得到运动目标节点位置的映射函数，从而得到运动目标节点的各个时刻位置。然后利用支持向量回归预测模型对目标节点进行位置预测，从而得出目标节点未来时刻位置动态预测。

1 SVM原理

支持向量机方法是建立在统计学理论的VC维理论和结构风险最小原理基础上的，根据有限的样本信息在模型的复杂性（即对特定训练样本的学习精度）和学习能力（即无错误地识别任意样本的能力）之间寻求最佳折衷，以期获得最好的推广能力。

在线性可分的情形下，设训练数据为：

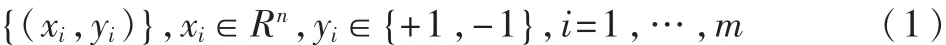
称训练集是线性可分的，如果存在一个超平面，使得：

称分类超平面ωTx+b=0是最优超平面。如果训练集到它的最小距离最大，或者说它使得分类间隙最大的平面显然超平面 ωTx+b=0是最优的。当（ω，b）且仅当是下面问题的最优解：

称训练集中的输入样本xi为支持向量，显然只有支持向量起作用，从而决定分类结果。

线性不可分就是某些训练样本不满足式（2），为此引入非负的松弛项ξi。与处理线性可分问题时的方法类似，构造最优超平面（广义最优超平面）的问题转换为求解下列优化问题：

其中，C＞0为正则化参数，用于控制对错分样本的惩罚程度，C越大，对错误的惩罚越重。

采用Lagarange乘子法，结合极值条件以及对特征空间的内积计算，从而可以得到回归函数：

2 SVM回归预测方法研究

2.1 节点的组织与路由

本文采用动态局部集中式组织方式。簇头在目标节点定位过程中通过一定的准则动态产生，其他节点将数据传送给动态簇头；在目标离开簇头侦测范围后，产生新的簇头，原来的簇头恢复侦测状态。初始区域或初始簇头的选择遵循以下原则：尽量减少信息贡献量少的节点或信息有冗余的节点的参与和通信能量的消耗，同时保证达到目标节点定位任务的精度要求。

2.2 支持向量机参数优化

在支持向量机的应用中，参数的选取对于结果的影响非常大。同样的条件，不同的参数可能导致的结果会截然不同。基于支持向量机的不稳定性，本文对支持向量回归机的参数进行了合理的选取和优化，主要对核函数中gamma函数g和损失函数ε进行参数寻优。

针对本文的支持向量回归机的训练样本及回归定位模型，参数g和ε的选取对训练样本的分类准确率有很大影响。将训练样本信息代入训练模型进行训练，建立两个循环让g和 ε在-210～210之间通过最优分类准备率的控制条件下选取最佳g和ε。MATLAB编写的寻找最佳g和ε部分代码如下。

2.3 支持向量回归定位方法

支持向量回归定位技术包括学习和定位两个阶段。学习阶段：首先通过采集已知节点位置信息和已知节点之间跳数信息作为训练样本，使用支持向量回归机技术得到连通信息到节点位置的映射函数，建立SVM定位回归函数。定位阶段：通过学习阶段建立的SVM回归定位模型，将运动目标节点接收到的跳数信息作为测试样本，使用建立的SVM定位回归函数来估计目标节点各个时刻位置。

本文采用由台湾大学林智仁博士等人开发的Libsvm进行回归训练，利用该工具实现多维输入一维输出的回归模型，完成了一维输出未知节点位置的要求。核函数的选择对数据的映射及测试样本的预测有很重要的影响，常用的核函数有多项式内核、径向基函数内核RBF和Sigmoind内核等。其中，高斯径向基核函数是应用最为广泛的核函数，具有很好的普遍性。因此，本文也采用高斯径向基核：

2.4 支持向量机回归定位方法具体描述

（1）初始阶段

节点部署完成后，利用典型的距离矢量交换协议，使网络中的已知节点之间接收到邻居节点的ID、跳数、位置等网络连通信息作为训练数据，将目标节点接收到的节点跳数信息和已知节点位置信息作为训练数据。

（2）学习阶段

将已知节点数据发送到簇头节点选取合理的路线发送回汇聚节点，当获得足够的训练样本后，执行回归训练，得到回归函数，从而建立了本文所需的回归定位函数模型。

（3）目标节点已知时刻位置估计阶段

最终，汇聚节点将回归函数发送到目标节点处，目标节点接收到汇聚节点发送的SVM信息后，目标节点根据自身存储的已知节点位置信息和网络连通信息作为测试数据，利用回归函数完成目标节点某一时刻的位置估计。

2.5 运动目标节点位置动态预测

无线传感器定位和预测方法中，误差累计和定位精度问题是衡量一种定位方法的重要标准。本文利用SVM回归定位方法对已知时刻运动目标节点进行定位，然后利用运动目标节点位置对未来时刻运动目标节点位置进行预测分析，两个步骤会产生误差累计问题以及SVM回归定位中定位精度定义问题。本文拟采用对SVM工具箱分类准确率和均方根误差进行阈值设定。

通过支持向量回归机定位模型函数测得一段时间的运动目标节点位置信息后，将运动目标节点位置信息和时间序列作为训练样本，利用上一步得出的最佳g和C建立SVM回归预测模型，从而完成对运动目标节点未来下一时刻位置预测。

3 仿真实验

为了检验算法的性能与本文提出的定位模型预测，本文实验在MATLAB平台下进行了仿真对比分析。网络部署假定为100 m×100 m区域，在该区域随机布撒节点。运动目标节点的坐标随机产生。

图1是在仿真区域内随机部署了100个节点。从图中可以看出利用SVM建立的回归模型下未知节点的真实位置与预测位置的误差值。通过对g和C参数优化选取最佳 C和 g参数，得出 best C=4.8，best g=0.000 39，best mse=1.860 8。从图中可以看出，本文提出的SVM回归模型得出未知节点的真实位置与预测位置之间的误差非常小，除去个别未知节点预测结果相差较大，其他未知节点预测结果稳定。平均定位误差达到一个很小的数值。

图1 目标节点的真实位置与预测位置的比较

图2是对试验区域的一个目标节点的位置利用SVM回归模型进行位置预测，节点从一个位置连续50 s内（每秒记录一次）移动，先对其物理位置进行定位，然后对目标节点未来10 s的轨迹进行预测，得出其位置模型。从图中可以看出，如果目标节点按照一条曲线运动，利用建立好的SVM回归模型对目标节点进行定位与预测，该算法稳定且准备，减小了定位误差。图3为目标节点根据前50 s的运动轨迹推导出来的未来10 s位置模型，由此完成了对目标节点未来时间段的位置预测（横坐标代表目标节点横坐标X值与运行时间）。

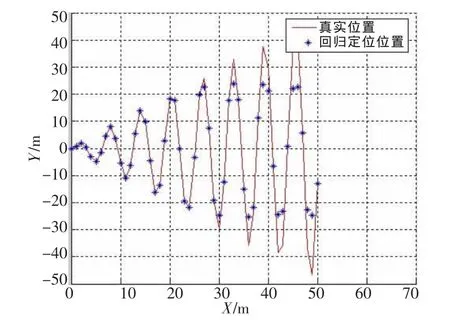
图2 SVM回归模型目标节点定位

图3 目标节点模型预测

本文分析了SVM回归算法在无线传感器网络节点定位中的应用方式，提出了一种改进的SVM目标位置跟踪预测方法。通过将节点位置信息和网络连通信息作为SVM回归训练样本，建立到目标节点位置的回归定位函数以及对未来时间段内目标节点的位置预测。理论分析与算法仿真结果表明，与传统的算法相比，本文提出的SVM回归定位算法模型提高了节点定位的精度，同时无需额外的硬件和功耗。本文提出的SVM回归预测模型对目标节点在未来时间段的位置预测在目标节点定位的实际应用中有一定的指导作用。

[1]孙利民，李建中，陈渝，等.无线传感器网络[M].北京：清华大学出版社，2005.

[2]ARORA A， DUTTA P， BAPAT S， et al.A line in the sand： a wireless sensornetwork fortargetdeteetion，classification，and tracking[C].Computer Networks the Int.J.Computer Telecommunications Networking，2004：605-634.

[3]Zhu Anfu， Jing Zhanrong， Yang Yan.Maneuvering target tracking based on ANFUS and UKF[C].2008 Intemational Conference on Intelligent Computation Technology and Automation， 2008：904～908.

[4]VAPNIK V.The nature of statistical learning theory[M].NewYork： Springer-Verlag， 1995.

[5]CORTES C， VAPNIK V.Support-vectornetworks[J].Machine Learning， 1995，20（3）： 273-297.

[6]WU Z L， LI C H， JOSEPH K Y N， et al.Location estimation via support vector regression[J].IEEE Transactions on Mobile Computing，2007，6（3）：311-321.

[7]NGUYEN X，JORDAN M，SINOPOLI B.A kernel-based learning approach to ad hoc sensor network localization[J].ACM Transactions on Sensor Networks，2005，1（1）：134-152.

[8]魏叶华，李仁发，罗娟，等.基于支持向量回归的无线传感器网络定位算法[J].通信学报，2009，30（10）：44-50.

[9]HEISELE B， PURDY HO， POGGIO T.Face recognition with support vector machines global versus componentbased approach[C].Proceedings of International Conference on Computer Vision， Vancouver， Canada，2001：688-694.