基于排队论的大型枢纽停车场规模研究
2013-09-28程林结晏克非
程林结,晏克非
(1.中国联合工程公司,浙江杭州 310014;2.同济大学,上海市 201804)
0 前言
枢纽停车场是综合枢纽作业系统的重要组成部分,是枢纽区交通流程的核心部分,具有不同于城市一般停车场的特点。枢纽停车场重点关注接送旅客以及出行旅客的流程,因此对便捷性要求很高,其方便程度将直接决定旅客是否愿意将车辆驶入停车场,而车辆是否进入停车场,又将直接影响枢纽交通流程的疏导效果及顺畅程度。影响停车场便捷性的最主要因素为停车场规模,停车场规模过大,造成资源浪费;停车场规模过小,高峰时刻停车供给紧缺,车辆寻找泊位的时间增加,还会在停车场入口处形成排队,进而影响周边动态交通。
1 停车场规模影响因素分析
枢纽停车场规模的影响因素众多,主要有以下几点。
(1)高峰时段车辆到达率:高峰小时车辆到达率是影响停车场规模最直接的因素。高峰小时进入停车场的车辆越多,即到达率越大,所需的泊位供给量就越大;反之就越小。
(2)高峰时段车辆平均停车时间:车辆逗留时间越长,泊位的周转率就越小,所需的停车泊位数就越大;车辆逗留时间很短时,泊位的周转率则较大,所需的停车泊位数就较少。
(3)车辆到达、驶离特性:车辆到达、驶离特性对停车场规模的影响并不是很直观,其对停车场规模的影响主要反映在泊位的利用率上。一般情况下,车辆到达、驶离越不均匀(即车头时距方差越大),泊位的利用率就越低,因此泊位需求量就越大;反之,则否。
(4)停车费用:从旅客角度来说,提高停车费用可能会促使一部分旅客采用其他交通方式进出枢纽,而不是自己开车进出枢纽。另外,停车价格的上升可能会抑制旅客的停车时间,增加停车场的周转率。
2 停车场规模计算方法
从上述分析可知,停车场规模受到众多因素的影响,但是在实际计算过程中,与停车规模直接相关的是停车场高峰时段车辆到达率、车辆到达离去特性分布、平均停车时间。
实际中可以将车辆进入停车场停车的过程看成一个排队系统,把停车场的入口看作排队服务的入口,每个停车泊位看做是一个服务台,车辆在泊位上停驶可以看作是排队接受服务,则停车场场的规模大小即为服务台个数。
2.1 排队理论计算方法
(1)排队系统
排队系统额可以抽象地描述如下:为了获得某种服务而随机到达的顾客,如果不能立即得到服务,允许按一定顺序排入队列,在顾客得到服务机构某一随机时间的服务之后,便离开系统。根据这些基本特征,排队系统可以分成三个部分,即输入过程、排队规则和服务机构。
a.输入过程
输入过程主要描述顾客的到达规律,这种规律可用到达间隔时间的概率分布来表示。如定长分布、泊松分布、爱尔朗分布等。
b.排队规则
排队规则主要描述顾客在队列中排列顺序的规定。通常有损失制、等待制和混合制三种方式。损失制指顾客到达时,若所有服务机构被占据,该顾客自动消失。
等待制指顾客到达时,若所有服务机构均被占据,则该顾客进入队列等待服务。混合制是一种损失制和等待制相结合的排队规则。如果队列长度超过一定的限制时,新到顾客自动离去,或等待时间超过某一限度时,队列中顾客自动离去。
c.服务机构
在排队系统有一个服务机构时,称为单通道排队系统,也可以有多个服务机构并行工作或串行工作,称为多通道排队系统或串行系统等。
停车场排队系统应为单通道排队、多窗口服务系统,同时上文分析得到服务时间服从泊松分布。
为了描述排队系统得特征,通常采用六参数符号系统,其一般形式如下:
A/B/C/D/E/F
式中:A——顾客到达过程的概率分布类型(如M表示泊松分布);
B——服务过程的概率分布类型(如M表示负
指数分布);C——服务台数目;
D——排队系统的最大容量;E——顾客源数;F——排队规则.一般当顾客源数为无限时,可从模型符号中省略。排队规则为先到先服务时也可省略。
假定停车场车辆到达服从泊松分布,服务时间服从负指数分布,服务机构为S,系统容量为k,则停车场排队系统可以表示为M/M/S/k。
(2)系统的数量指标(以M/M/S/k为例)
M/M/S/k排队模型为泊松输入、负指数分布服务、S个服务台、系统容量为k的混合制系统。假定顾客到达率为λ,每个服务台服务率为μ,则整个系统得最大服务率为Sμ,令ρ=。
a.系统空闲的概率P0

Pk就是顾客被拒之于系统之外的概率,称为损失率。
2.2 排队论在停车场中的应用
在实际中,车辆到达停车场时,若有空闲停车泊位则车辆进入泊位停驶,若没有空闲车位则车辆离去。因此,在进行停车场规模研究时,可以将停车场泊位数(服务台数)C作为服务台数以及系统容量,即S=k=C。设车辆到达率为λ,每个泊位服务率为μ,则整个系统得最大服务率为cμ,令ρ=。给定系统损失率不超过5%,计算满足此条件的最佳值C*,此值即为停车场规模。

f(C*)≤5%≤f(C*-1)
即fC*≤5%≤f(C*-1)
其中:
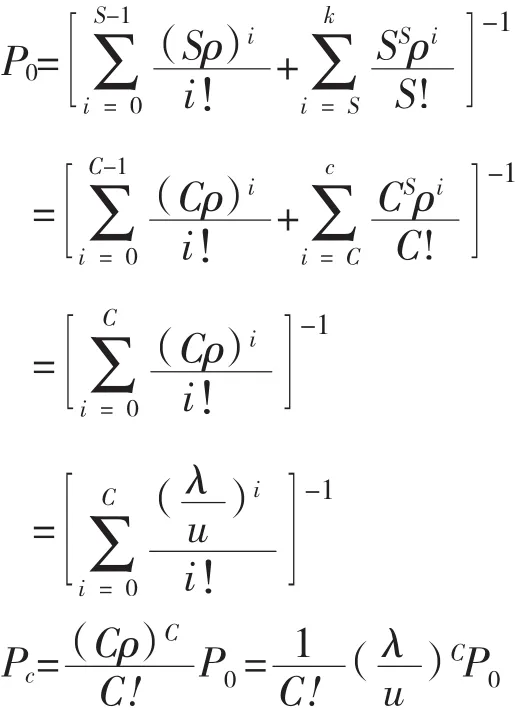
对C=1,2,3…分别求PC,根据5%落在哪个不等式的区间内来定出C*。
该问题的关键在于如何求解C的最佳值C*。在计算过程中会碰到两个难点:
一、如果从 C=1,2,3…依次计算 PC,当 C*较大时,要计算的次数非常多,工作量相当之大,而且都是重复计算,大大降低了工作效率;
二、从PC的表达式中,可以看出,其中包含了C!以及()C两种表达式,当C*值很大时,在计算机中进行计算会产生溢出,特别是C!项。关于阶乘的计算,目前计算机的配置最大只能算出170!,当C值超过170时,计算机是无法计算出C!的结果的。
要想使该理论在实际中得到更广泛的应用,必须很好的解决上述两个问题。这就要求我们一方面对PC的表达式进行分解处理,化成计算能计算出来的形式;另一方面尽量减少PC值的计算次数,降低计算量。对于这两个问题的解决方法,将结合虹桥枢纽的案例进行阐述。
3 案例分析
上海虹桥机场位于上海市西郊长宁区的西南方位置,毗邻闵行区。目前,虹桥机场投入使用的社会停车场主要有两个,第一停车场位于候机楼前,为地面露天停车场,经过多次改造,停车泊位已由506个增加至970个。第二停车场可用面积5 000多m2,有100多个停车位,其中30多个旅游巴士车位,其他全是小型车位,主要停放内部人员的车辆。本文主要研究第一停车场。
通过虹桥机场停车场管理系统收集的数据可得,停车场高峰小时车辆到达率为350 veh/h,车辆平均停车时间为150 min。通过车辆到达时刻数据分析可得车辆到达服从泊松分布。
根据前面的叙述,将车辆进入停车场停车过程看做是一个排队系统,车辆停车过程看成顾客在系统中接受服务,排队规则为损失制。设停车场的泊位数为c,则停车过程M/M/c/c为排队模型。到达率λ=350 veh/h,单个泊位服务率 μ=60/150=0.4,==875。给定系统损失率不超过5%,计算满足此条件的最小C*值,此值即为停车场规模。
此问题的数学模型为:
(fC*)≤5%≤(fC*-1)
即fC*≤5%≤(fC*-1)
其中:

对C=1,2,3…分别求PC,根据5%落在哪个不等式的区间内来定出。
此问题的关键在于PC的求解,不难发现PC的表达式中含有C!以及875C这两项,在值较小的情况下,我们不难算出其值,而当值较大时,计算机在计算值时会产生溢出,在目前的计算机硬件配置前提下,计算机中双精度浮点型变量表示的数值范围为 -1.797 69×10308~1.797 69×10308,因此,计算机能计算出其阶乘的最大数值为170,超过170的数值计算机无法计算出其阶乘。在计算875C时更是只能算出C≤104的情形。另外在求C*时,若从 C=1,2,3…分别求 PC,则要计算 847 次才能得出结果,计算非常繁琐,大大降低了工作效率。本文借助计算机编程来解决这两个问题。
(1)PC的求解
将P0代入PC中得到:

由于PC分母中含有C+1项,先因此考察其倒数1/Pc:

a(0)=1
a(1)=a(0)*C/875
a(2)=a(1)*(C-1)/875
…
a(i)=a(i-1)*(C-i+1)/875
…
a(c)=a(c-1)*/875
最后计算各个数组元素之和即可得到1/Pc的值,进而得出PC,这样就巧妙地避开了计算C!以及875C这两项超出计算机计算范围的表达式。PC计算程序代码如下:
Public Function Pc(c As Integer,b As Double)As Double
Dim i As Integer,P As Double
ReDim a(c) As Double
a(0)=1
P=0
For i=1 To c
a(i) =a(i-1)*(c-i+1)/b
Next i
For i=0 To c
P=P+a(i)
Next i
P=1/P
Pc=P
End Function
程序中函数Pc的值即为需要计算的损失率PC,参数c和b分别为服务台数C以及λ/μ的值,将C和λ/μ的值作为形式参数调用函数Pc即可求出损失率PC。
(2)C*的求解
上面已经介绍了损失率PC的求法,下面介绍C*的求法,若如前所述,从 C=1,2,3…分别求 PC,然后将满足fC*≤5%≤f(C*-1)的C做为C*的值的话,则要计算很多次才能得出结果,此例需要计算847次。因此借助计算机程序语言中的循环算法来解决问题,让计算机自动求解C*,这样大大减少计算量。编程的思路为:先假设C=1,计算此时的PC,然后判断是否满足PC*≤5%,若不满足则让C自动加1,使C=2,再判断…直到PC*≤5%时返回此时的C值,即为所求的停车场规模值C*。具体程序代码如下:
Private Sub CommandButton2_Click()
Dim c As Integer,i As Integer,b As Double,P As Double,f As Double
b=Range("B7")
f=Range("B6")
c=1
P=0.99
Do While P>=f
c=c+1
P=Pc(c,b)
Loop
Range("F10")=c End Sub
通过计算可得,当C=846时,PC=0.050 3,当C=847时,PC=0.049 4,因此,在损失率不超过5%的条件下,最佳停车场规模值C*=847。
4 结论
论文将排队论引入枢纽停车场系统,提出了计算枢纽停车场规模的新方法,同时给出了算法的求解过程,为枢纽停车场建设提供了新的依据。但是论文仅对车流泊松到达的情况进行了研究,要想更全面的解决问题,应在此基础上,对其他特性的到达车流进行研究。
[1]吕慎.城市客运交通枢纽规模研究[J].深圳大学学报理工版,2005(2):181-182.
[2]何宁.综合交通枢纽规划和需求分析方法[J].城市交通,2006(5):15-16.
[3]黄坤鹏.火车站综合交通客运枢纽客流与设施容量预测分析[J].交通标准化,2009(1):122-123.
[4]傅家良.运筹学方法与模型[M].上海:复旦大学出版社,2005.
[5]高金华,侯丽华.大型机场停车设施规划研究[J].中国民航大学学报,2007,25(4):35-39.
[6]王殿海.交通流理论[M].北京:人民交通出版社,2002,13-18.
[7]覃峰.排队论在停车场设计中的应用[J].交通管理,1998(2):16.
[8]陈峻.城市停车设施规划方法研究[D].南京:东南大学,2000.
