基于ADS的微带线不连续性分析与应用*
2013-09-28吉建华孙雨耕2贾伟广
吉建华,孙雨耕2,贾伟广
(1.天津大学仁爱学院信息工程系,天津301636;2.天津大学电气与自动化工程学院,天津300072;3.国家海洋标准计量中心,天津300112)
1 引言
微带线作为一种最常见的平面传输线,易与其他无源和有源的微波器件集成,并且方便加工,是PCB上元器件互连的主要传输线之一,已广泛应用在各种射频电路中。在实际电路布线时,由于印刷板大小的限制,常需要做弯折走线处理,即在PCB中会出现微带线拐角,它属于典型的微带线不连续结构之一[1]。由于微带电路尺寸与工作波长可以相比拟,所以这种不连续性会引入寄生电抗,从而引起相位和振幅误差、输入与输出的失配,以及可能存在的寄生耦合,进而导致电路性能的恶化,影响PCB电路信号的传输特性。文献[2-3]分别采用混合有限差分法和FDTD与坡印廷法相结合的方法定量分析了微带线不连续性对信号的影响,但并未提出解决方案。文献[4-5]分别采用保护带和失真系数的方法对微带线不连续性进行了模拟分析,但并未将结论运用于实际电路中。文献[6]利用平衡法来对抗微带线不连续性带来的插入损耗过大的问题,但使用范围有限。设计射频电路时,消除微带线不连续性的常用方法是采用圆弧拐角或对导带切角直接补偿不连续性[7-9],以使其不连续性效应最小。导带切角大小可由经验公式[10]计算求得,但该计算结果与实际误差较大。本文在此经验公式的基础上,通过ADS仿真分析不同弯折走线对电路性能的影响,找到何种拐角最有利于信号的传输,并将其应用到实际电路中。
2 微带线不连续性分析
当微带线尺寸W/h和介质层介电常数εγ给定时,其特征阻抗就是确定的。对于如图1所示的均匀微带线而言,微带线上沿传输线纵向的任何一处特征阻抗都是相等的。当PCB信号沿均匀微带线传输时,它本身不会引起信号的反射,对信号传输特性不会产生影响。
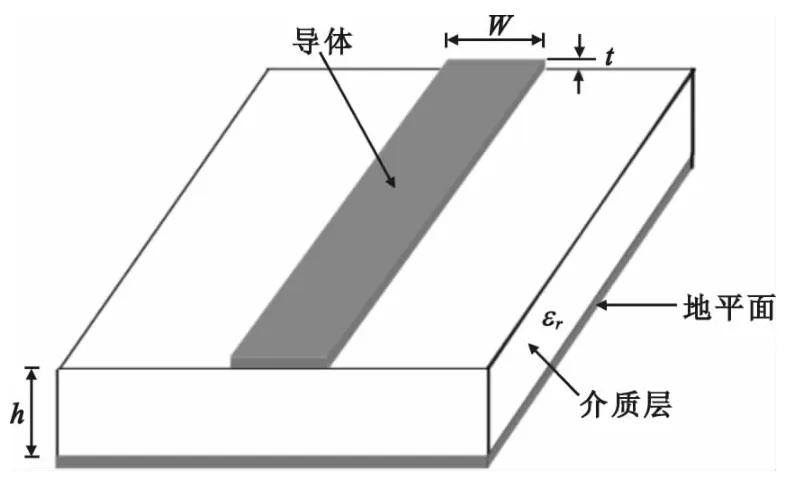
图1 微带线几何结构Fig.1 The geometric structure of the microstrip
图1 中W为微带线宽,h为介质板厚度,εγ为介质层介电常数,t为敷铜厚度。
但是,当PCB需要弯曲走线时,微带线拐角处的线宽会发生变化,从而导致特征阻抗发生变化。由于微带线在经过拐角时宽度变宽,拐角附近的导带面积增大,存在着电荷积聚效应,导致弯曲处走线与参考层之间的电容增大,走线的特征阻抗减小,因此微带线直角弯曲处呈现出特征阻抗的不连续性,从而导致微带线上信号产生反射,影响信号的传输特性。不同结构尺寸的微带线直角弯曲对信号传输特性的影响程度不同,直角拐角是PCB走线布局中较为常见的一种结构,等效电路为T网络[11],如图2所示,其等效电容(C)和电感(L)分别由式(1)和(2)给出。
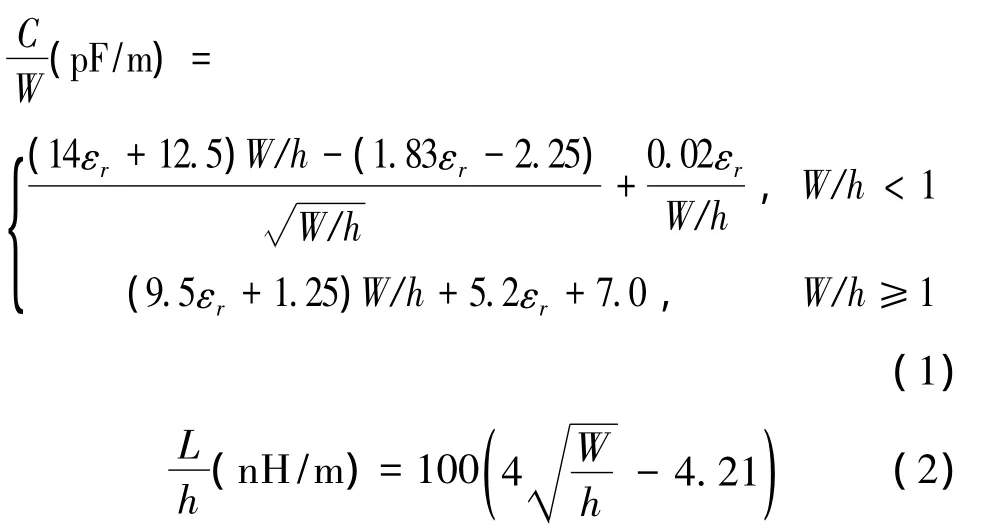
式中,W为微带线宽,h为介质板厚度,εγ为介质层介电常数。
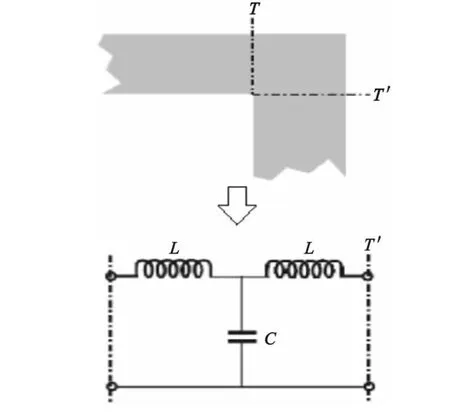
图2 直角拐角等效电路Fig.2 Equivalent circuit of right-angle bend
在实际电路中,消除这种微带线不连续性的最常用方法是采用圆弧弯曲或对导带切角直接补偿其不连续性。采用圆弧弯曲走线时,在圆弧半径R足够大的情况下,走线宽度几乎未发生改变,基本可以消除微带线的不连续性效应。但是这种方式一般都要求圆弧半径大于走线宽度的3倍,即R>3W,这会使得微带线在PCB上占据空间加大,因而在实际PCB布线中并不常用。而切去微带线拐角的一角是减小其不连续处传输和反射特性的一种常用方法。对微带线进行切角处理可以减小拐角处的等效电容,从而补偿微带线直角弯曲的不连续性效应,并且这种方法可应用于任意张角的拐角。
有研究表明[12-13]:微带线直角弯曲时采用 45°外斜切方法是控制微带线特征阻抗连续性的最佳方法,它能够很好地改善信号传输特性。45°外斜切结构示意图如图3所示。
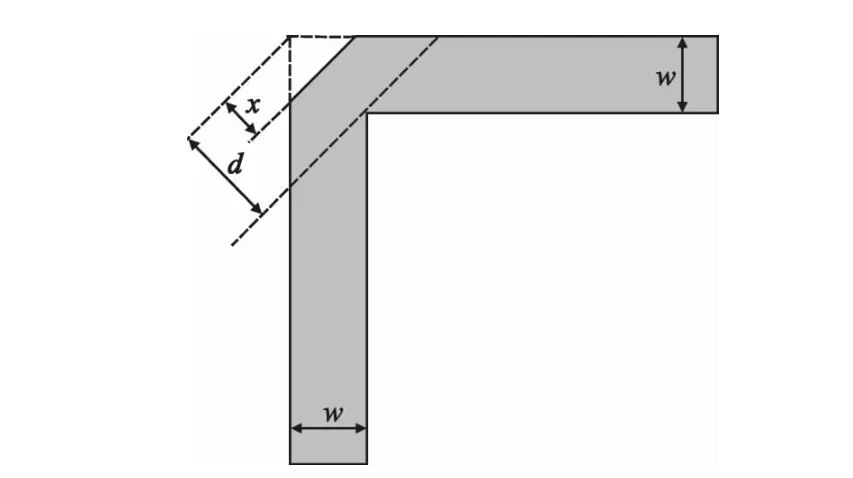
图3 45°外斜切示意图Fig.3 Schematic diagram of the 45°out miter bend
图3 中,d表示微带线直角弯曲内拐角至外拐角的距离,x表示切角处至外拐角的距离,一般常用M=x/d表示拐角斜切率。拐角斜切率的大小表示微带线被切割的多少,它对微带线的传输特性有显著的影响,直角弯曲外斜切存在最佳斜切率。一般而言,当斜切率为最佳斜切率时,直角拐角处的特征阻抗不连续性最小,信号传输特性最佳。
当基板相对介电常数εγ取值在2.5~25范围内,直角弯曲外斜切的最佳斜切率M与W/h之间的关系式近似为
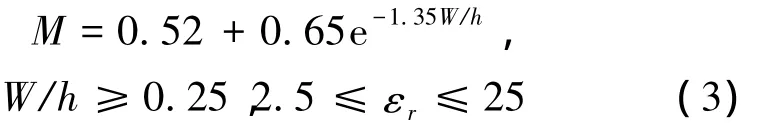
根据这一经验公式计算最佳斜切率可以大大提高PCB设计效率,从而降低设计难度。然而,根据经验公式得到的计算结果与实验结果之间仍会存在误差。因此,在实际PCB布线设计中,可以先根据经验公式计算得出最佳斜切率,然后在此基础上利用辅助仿真工具ADS进行仿真验证。
3 ADS仿真分析
为了分析微带线不同拐角对PCB信号传输质量的影响程度,将微带线看成二端口网络,每一端口均与PCB微带线的50 Ω特征阻抗匹配,仅考虑走线拐角变化对信号传输质量的影响。这样就可以利用二端口网络的散射参数S11和S21来评价不同拐角的传输特性,从而反映信号传输质量的差异。其中S11表示端口2接匹配负载时端口1的反射系数,即由于微带线特征阻抗不连续造成的信号反射程度,S21表示端口2接匹配负载时信号从端口1向端口2传输的传输系数。
利用ADS对图4给出的几种常用的微带线拐角进行建模仿真,其中微带线的基本参数设置为:基板厚度 h=20 mil,介电常数 εγ=3.6,覆铜厚度 T=1.8 mil,其他参数按默认设置,仿真频率范围为0~12 GHz,仿真结果如图5所示。由仿真结果可以看出:在相同频率范围内,不同形状微带线拐角的传输特性也不同,45°外斜切拐角回波损耗最小,圆弧拐角(R=3W)次之,直角拐角最大,即传输特性呈现优良的次序依次为:直角拐角<圆弧拐角(R=3W)<45°外斜切拐角。由仿真结果可知:在小于1 GHz的频率范围内,3种拐角方式的反射系数S11均小于-40 dB,微带线拐角的几何结构对信号传输特性S21影响很小,但随着频率的提高,其影响显著增强,特别是直角拐角。由此可以得知微带线拐角采用45°外斜切的几何结构,其传输性能优于其他结构拐角,微带线对信号传输特性的影响相对较小。
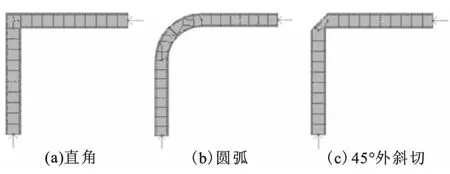
图4 微带线拐角Fig.4 The bends of microstrip

图5 不同微带线拐角的反射和传输特性Fig.5 Reflection and transmission characteristics of different microstrip bends
另外,通过查看不同拐角处的电流分布也可以验证最佳斜切率的存在。图6(a)给出了直角拐角处的电流分布,可以看到微带线外拐角处电流近乎为零,而内拐角处电流最大,电流要流经最短路径,从而集中在了内拐角处。图6(b)为M=0.5时的电流分布,微带线外拐角处有微弱电流流过。图6(c)为M=0.576时的电流分布,这时微带线外拐角处的电流分布与均匀微带线上的电流分布几乎是连续的。

图6 不同微带线拐角的电流分布Fig.6 The current distribution of different microstrip bends
4 研究结果应用
对于5.8 GHz RFID阅读器而言,射频电路选用的是介电常数为 εγ=3.6的Rogers4350板材,特征阻抗为50 Ω的射频走线,W/h=2.17。由式(3)可得其外斜切最佳斜切率M=0.555。对于不同的斜切率,45°外斜切拐角的反射和传输特性的仿真结果如图7所示。图7表明:外斜切拐角的斜切率不同,对应外斜切拐角的信号反射特性也不同,而传输系数S21在小于8 GHz的频率范围内差别很小。

图7 不同斜切率拐角的反射和传输特性Fig.7 Reflection and transmission characteristics of different percentage miter bends
由图7可知,对于工作在5.8 GHz的RFID阅读器电路而言,当M=0.576时,反射系数S11最小,即反射特性最佳,尽管这时M取值与经验公式(3)计算结果不完全一致,但在文献[12]所给的误差范围内。
图8为加工制作完成的5.8 GHz RFID阅读器射频电路中的一处直角拐角,采用的是由仿真得到斜切率为M=0.576的45°外斜切拐角。实践证明采用上述方法,可以最大限度降低PCB走线中的弯折对信号传输带来的影响。

图8 阅读器PCB走线中的45°外斜切拐角Fig.8 45°out miter bend in reader PCB
5 结论
不同几何形状的微带线拐角对PCB信号传输特性的影响是不同的,虽然根据经验公式可以计算得到直角拐角的斜切率,但其与实际电路误差较大。
文中在经验公式的基础上,利用ADS仿真总结出了不同微带线拐角的传输特性。不同形状微带线拐角的传输特性呈现优良的次序依次为直角拐角<圆弧拐角(R=3W)<45°外斜切拐角。对于已选定的板材,根据经验公式结合ADS仿真,可以得到在其工作频率处所对应的45°外斜切拐角最佳斜切率,进而将其应用到实际射频电路PCB设计中。当不同的PCB板材工作在不同频率处的不同射频电路中时,可以利用此方法得到其所对应的45°外斜切拐角最佳斜切率,但该方法只适用于板材和工作频率均已确定的电路设计。
[1]清华大学《微带电路》编写组.微带电路[M].北京:人民邮电出版社,1976:89-96.The microstrip circuit compilling group of Tsinghua University.Microstrip Circuit[M].Beijing:The People's Posts and Telecommunications Press,1976:89-96.(in Chinese)
[2]王胜源,李玉山,曹剑中.混合有限差分方法及其在微带电路分析中的应用[J].仪器仪表学报,2012,31(7):1552-1557.WANG Sheng-yuan,LI Yu-shan,CAO Jian-zhong.Hybrid finite diference method and its application in microstrip circuit analysis[J].Chinese Journal of Scientific Instmment,2012,31(7):1552-1557.(in Chinese)
[3]毛剑波,黄正峰,杨明武,等.微带线不连续性辐射研究[J].电子测量与仪器学报,2012,26(5):392-397.MAO Jian-bo,HUANG Zheng-feng,YANG Ming-wu,et al.Study on microstrip discontinuity radiation[J].Journal of Electronic Measurement and Instrument,2012,26(5):392-397.(in Chinese)
[4]权赫,孙兆牛.抑制非平行微带线间串扰的保护带方法研究[J].电子测量与仪器学报,2011,25(10):850-856.QUAN He,SUN Zhao-niu.Research on guard band to reduce the crosstalk for non-parallel microstrip lines[J].Journal of Electronic Measurement and Instrument,2011,25(10):850-856.(in Chinese)
[5]张栋.微带线直角拐角脉冲信号传输特性分析[J].电子科技,2010,23(1):26-28.ZHANG Dong.Research into Transmission Properties of Impulse signal in Microstrip Bend[J].Electronic Science and Technolgy,2010,23(1):26-28.(in Chinese)
[6]彭玉峰,林思宏,张淑莉,等.基于平衡技术的微带低通滤波器版图优化设计[J].现代电子技术,2012,35(4):27-28.PENG Yu-feng,LIN Si-hong,ZHANG Shu-li,et al.Design of microstrip low-pass filter layout optimization based on balanc technology[J].Modern Electronics Technique,2012,35(4):27-28.(in Chinese)
[7]陈鹏,曹沐昀.微带线不连续性补偿方法仿真研究[J].电子科技,2013,26(3):119-121.CHEN Peng,CAO Mu-yun.Simulation and Analysis of Different Compensation Methods of Microstrip Line Discontinuity Based on HFSS[J].Electronic Science and Technolgy,2013,26(3):119-121.(in Chinese)
[8]陈慰,赵娜,陶学敏.微带线不连续性补偿方法的HFSS仿真分析[J].现代电子技术,2011,34(13):92-94.CHEN Wei,ZHAO Na,TAO Xue-min.HFSS Simulation and Analysis of Microstrip Discontinuity Compensation Method[J].Modern Electronics Technique,2011,34(13):92-94.(in Chinese)
[9]Pozar D M.微波工程[M].3版.张肇仪,周乐柱,吴德明,等,译.北京:电子工业出版社,2006:168-174.Pozar D M.Microwave Engineering[M].3rd ed.Translated by ZHANG Zhao-yi,ZHOU Le-zhu,WU De-ming,et al.Beijing:Publishing House of Electronics Industry,2006:168-174.(in Chinese)
[10]路宏敏,吴保义,姚志成,等.微带线直角弯曲最佳斜切率研究[J].西安电子科技大学学报(自然科学版),2009,36(5):885-889.LU Hong-min,WU Bao-yi,YAO Zhi-cheng,et al.Research on the optimal percentage miter of the microstrip right angle bend[J].Journal of Xidian University(Natural Science Edition),2009,36(5):885-889.(in Chinese)
[11]Jia Shenghong,Lancaster M J.Microstrip Filters for RF/Microwave Applications[M].New York:John Wiley & Sons,Inc.,2001:89-93.
[12]Douville R J P,James D S.Experimental Study of Symmetric Microstrip Bends and Their Compensation[J].IEEE Transactions on Microwave Theory and Technology,1978,26(3):175-182.
[13]Feix N,Lalande M,Jecko B.Harmonic Characterization of a Microstrip Bend via the Finite Difference Time Domain Method[J].IEEE Transactions on Microwave Theory Technology,1992,40(5):955-960.
