基于变形模板的复杂截面轮廓重构方法研究

玉荣， 徐 金 亭， 孙 玉 文＊

（1.大连理工大学 机械工程学院，辽宁 大连 116024；2.大连理工大学 汽车工程学院，辽宁 大连 116024）

0 引 言

基于测量数据的截面轮廓重构一直是计算机辅助几何设计、计算机图形学领域的研究热点［1－3］，也是各类复杂曲面构造方法如蒙皮、扫掠、回转及放样等操作的前提基础.传统的截面轮廓曲线重构方法可分为两类：对测量数据的插值和对测量数据的逼近.对散乱截面数据的插值或逼近而言，散乱数据的分割及序化处理、参数化方法的选择、节点矢量的确定、曲线控制点的反算等都是截面轮廓曲线重构的关键步骤，任何一步处理不当都会导致最终的截面曲线无法反映真实的截面轮廓［4－5］.目前，多数研究集中于上述某一关键步骤的处理，如散乱数据的参数化、节点矢量的优化等方面［6－7］.影响因素的多变性在带来了造型的灵活性的同时，也增加了很大的不确定性，往往需要手工参与，促使新的造型技术的发展.最近，基于设计模板的轮廓曲线构造方法在医疗图像及制造工程中逐渐受到重视并成为新的研究热点［8］.如，叶片等复杂曲面零件因在负载及应力等工况下长期运行，会产生不同程度的变形，导致其实际的几何形状与名义几何模型存在较大误差.在获取实际叶型截面轮廓时，如能以设计模板为基础，通过模板变形进行截面轮廓重构，不仅可以避免实测散乱数据的序化处理、参数化和节点矢量优化等传统步骤，在快速实现散乱数据的精确轮廓重建的同时，还能建立起设计模板与实际截形之间的解析关系，精确判断零件的变形情况，从而用于指导零件形状的校正工艺，使得用于叶片等零件破损区域修复的截形更为合理.

当前，基于变形模板的曲线重构中，变形模板主要采用离散数据表达形式，有些B样条形式表达的设计模板在变形时往往不能定量给定最大变形量的幅值，这给变形模板的精确表达和对模板变形的定量控制带来不便.为实现这一目的，本文提出一种基于变形模板的复杂截面轮廓重构新方法.在建立的模型中，采用能够实现单点或多点变形量精确控制的B样条曲线变形策略.首先，通过精确的刚性配准使得设计模板与实测点集尽量贴合，进而采用精配准与模板变形迭代进行的方式，使模板与实测点集最大限度地重合，在将重构误差控制在允许范围内的同时使模板的变形最小化.

1 变形截面轮廓重构的数学模型

基于模板变形的截面轮廓重构是基于给定的截面模板曲线D（u）和对应的实测零件截形数据点集｛Qi｝n1，在模板变形最小的条件下使得实测点与变形后的模板曲线间的几何误差最小.具体的重构过程主要包括数据点和设计模板曲线的给定、设计模板与实测点的刚性配准以及模板变形与配准迭代优化等主要过程.在本章中，将首先提出基于变形模板的截面轮廓重构的数学模型.

一般情况下，截面模板曲线可由B样条曲线描述，其数学表达式为

式中：di为第i个控制顶点；Ni，k（u）为B样条曲线的基函数，k为样条基的次数.对于一测量点Qi，可定义其到模板曲线的距离函数如下式所示：

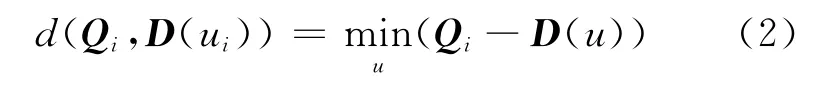
而变形模板与实测点之间重构就是实现测量点到模板曲线间的误差最小.根据式（2）及最小二乘原理，变形模板与实测点之间重构的目标函数可写为

式中：f（Δd）为模型必须满足模板变形的最小条件；Δd为模板变形后的控制点变动量；E为配准时的变换矩阵为变形后的模板曲线，

利用上述模型进行重构时，首先采用刚性配准使模板与实测点最大限度地贴合.在此基础上，再采用模板变形与精确配准迭代的策略实现模板与实测点的最终贴合.其中，在迭代中交替计算时限定模板变形量的约束点可按下式给出：

式中：Dj（u）为与测量数据Qj在模板曲线上的对应点；Δt为一小量.一般情况下，模板曲线的变形可取一点或多点约束.

2 实测数据的精确配准及优化算法

2.1 实测数据与模板曲线间的配准模型

在基于模板变形的曲线重构中，实测数据与模板曲线间的精确配准可以被描述为求解测量数据到模板曲线距离的平方和相对于刚体变换6个参数的极小值问题.因此，可以根据最小二乘原理构造如下的目标函数：

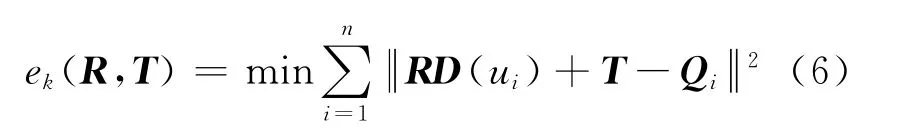
式中：D（ui）为Qi在给定曲线D（u）上的对应点；R为由绕坐标轴的3个旋转量α、β、γ构成的旋转变换矩阵；T为沿坐标轴的3个平移量tx、ty、tz构成的平移矢量.目前所提出的优化上述目标函数的迭代方法，如ICP算法［9］、Menq算法［10］等大都采用轮换变量法，即计算点到曲线的最近点和求解旋转、平移变换，对迭代过程进行优化处理，可在保证定位精度的同时加快迭代过程向全局最优的收敛速度，特别适用于复杂曲线的配准定位问题［11］，因此本文也采用轮换变量法.具体优化过程如下：首先给定初始变换估计R0、T0，并将其作为迭代过程的初始值，进而计算出点｛Qi｝n1在模板曲线上的最近点作为初始目标点［11］；然后利用轮换变量法进行迭代优化.在每一次迭代过程中，都计算目标函数ek，同时检查迭代终止准则

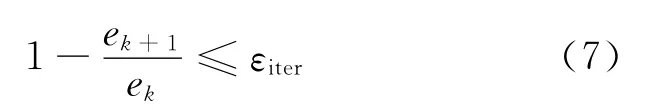
式中：εiter为给定计算精度.如果终止准则成立，则结束迭代，得到最优定位变换Ropt、Topt；否则迭代继续进行.经过上述优化处理，就实现了测量数据与模板曲线之间的精确定位.

2.2 点到B样条曲线的最近点计算

在计算点到曲线的最近点时，通常采用的方法是数值迭代法.此类方法可达到很高的计算精度，但对初始值的要求却比较苛刻，如果初始点选择不当，迭代过程可能会陷入局部极值甚至根本无法收敛.为解决这一问题，本文提出了一种新的基于伯恩斯坦多项式算术运算［12］和递归细分的最近点计算方法.

由于B样条曲线可以采用节点插入的方式方便地转化为Bézier曲线，不失一般性，下面将以Bézier曲线为例推导点到曲线最近点计算的数学模型，进而再将其推广到B样条曲线.数学上，一条m次Bézier曲线可以表示为一段伯恩斯坦多项式函数曲线：

式中：bi为Bézier曲线r（u）的控制顶点；Bi，m（u）为伯恩斯坦基函数；u为曲线的参数；m为曲线的次数.对于一点p0，它到曲线r（u）的平方距离函数可定义如下：

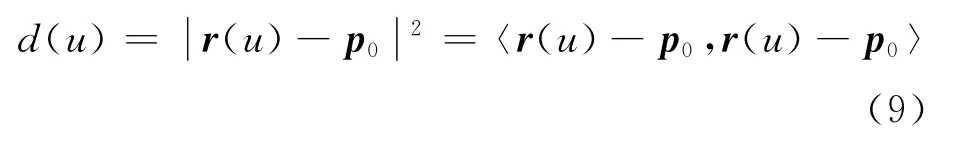
求解d（u）局部极小值的一般方法是，计算距离函数的导数函数（u）的所有零点，并检查在这些零点处d（u）是否达到最小.对于非线性方程（u）＝0而言，可利用Newton－Raphson或其他数值迭代优化方法进行求解.然而，实际的计算表明此类迭代方法即便事先给定很好的初始值，仍有可能出现计算错误［13］.为此，本文将充分利用德卡斯特里奥算法和Bézier曲线的凸包性质进行求解，以避免求解过程对初始值的依赖.

利用伯恩斯坦多项式算术运算及基函数的规范性，可将（u）改写为一伯恩斯坦多项式s（u）：

式中：gi∈R，为多项式s（u）的伯恩斯坦系数.为了得到更为直观的数学模型，利用伯恩斯坦基函数的线性精度性质，函数s（u）在u参数轴上的图形可由如下式所示的一条Bézier曲线表示：

式中：gi∈R2，是Bézier曲线rs（u）的控制顶点.

从上面的推导过程可以看到，如果方程（u）＝0成立，则曲线rs（u）必与u轴相交.这样，点到曲线的最近点计算问题就转化为直观的曲线与参数轴之间交点的计算问题.对于B样条曲线，可先将B样条曲线转化为一组Bézier曲线，然后对每条Bézier曲线应用上述方法，通过比较计算确定点在B样条曲线上的最近点.图1给出了一个B样条曲线Bézier曲线细分和最近点计算的算例.

图1 B样条曲线Bézier曲线细分及最近点计算的算例Fig.1 An example of B－spline curve subdivided by Bézier curve，and closest point calculation

2.3 旋转和平移变换矩阵的计算

设Q＝ ｛Q1，Q2，…，Qn｝为测量点集，P＝｛P1，P2，…，Pn｝为Q在模板曲线上的对应点集，其中Qi和Pi为一对匹配点.假设满足式（6）的最小二乘解为Rr和Tr，则点集P′＝ ｛P′i｜P′i＝RrPi＋Tr｝和Q具有相同的质心，即CP′＝CQ.其中

这样，旋转平移变换可分为两步计算：（1）计算使式（13）取得最小值的旋转变换R；（2）按T＝CQRCP计算平移矢量.本文将采用Arun等提出的采用奇异值分解法（SVD）［14］求解使方程式（13）取得最小值的旋转变换矩阵R.首先计算P和Q之间的协方差矩阵

对H进行奇异值分解可得H＝UΛVT，X＝VUT，计算行列式det（X），如果det（X）＝＋1，则旋转矩阵R＝X［15］，求得旋转矩阵后，进而求解平移矢量T.

3 模板曲线的约束变形

B样条曲线的单点约束、多点约束变形要通过计算曲线控制点的变动量来达到所要求的变形，这可由最小二乘法重新配置控制点来实现［15］，具体计算过程如下.将变形后的模板曲线写成矩阵的形式，可以得到

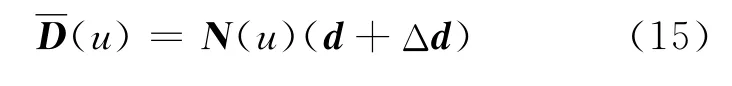
式中：N（u）为基函数向量，N（u）＝（N0，k（u） …Nn，k（u））；d为控制点向量，d＝（d0…dn）；Δd为控制点扰动向量，Δd＝（Δd0… Δdn）T.

对于复杂的物体，一般需移动多点才能达到所要求的变形.假设曲线有m＋1个初始点，它们对应的参数分别为uj（j＝0，1，…，m），则模板曲线多点约束方程可写为

根据式 （15）中各变量的含义，并令 ΔD＝（ΔD0… ΔDm）T，则式（16）可改写为如下的矩阵形式：

可以通过计算矩阵N（u）的广义逆即N（u）的方式求解上述最小二乘问题，即Δd＝N（u）ΔD，从而使模板曲线控制点扰动量Δd达到最小［16］.对于秩为r，（m＋1）×（n＋1）的矩阵N（u）而言，其秩分解为

式中：R是秩为r的（m＋1）×r矩阵；S是秩为r的r×（n＋1）矩阵.则矩阵N（u）的广义逆可写为

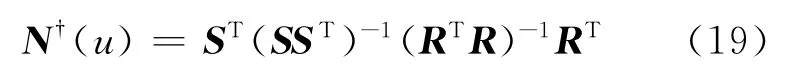
将式（19）代入Δd＝N（u）ΔD即可得到最小二乘意义下的控制点扰动量Δd.需要注意的是，矩阵N（u）的秩分解并不是唯一的，但任意两种分解所得的广义逆矩阵却是相同的，上述求解方法既可用于欠定线性方程组，也可用于超定线性方程组.

特别地，当是单点约束时，模板曲线约束方程可直接写为

式中：D0为模板曲线D（u）上参数为u0的点为变形后模板曲线上相应的目标点；ΔD0为目标点与初始点的位移.对于单点约束，由于矩阵N（u）的秩为1，它的广义逆为

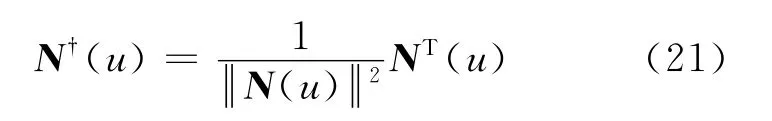
令ΔD＝ΔD0，N（u）＝N（u0），则式（17）的解可表示为

基于上面的计算公式，图2（a）给出了单点约束时B样条曲线变形，图2（b）为多点约束时B样条曲线变形的情况.

图2 两种B样条曲线变形的算例Fig.2 Two types of B－spline deformation′s examples

4 实例验证

为验证所提出的基于变形模板的截面轮廓重构模型及方法的有效性，本文针对叶片曲面进行了重构实验.如图3所示，算例中的截面轮廓为叶片截形.从图中可以看到，配准前设计模板与实际截形的空间位置相对误差较大，设计模板和实际截形间的最大距离为9.78mm，截形弦长500 mm，重构中实际截形的采样点为100个.图3给出了经过配准后的设计模板和实际截形的相对位置.图4分别给出了基于模板变形的截面轮廓重构过程中经过第1、2、6、26、36次迭代时设计模板与实际截形的相对位置.从表1也可以看出，设计模板的形状在不断演化，且同实际截形的误差（误差以设计模板与实际截形间的最大距离表示）在逐步减小，这表明所提出方法具有充分的形状变化适应性.同时，由于模板变形和精确配准的交替迭代使用，最大限度保证了模板在尽可能小的变形条件下实现与实际截形的贴合.所提算法已经在Visual C＋＋中编码实现，经过36次迭代计算时，设计模板与实际截形之间最大误差仅为0.001 mm.此外，该算法采用迭代求解的方式是为了减少设计模板的变形程度，同常规曲线重构的迭代求解以减少拟合误差一样，会增加程序的运行时间，但运行时间（CPU 2.33GHz，内存4GB）在毫秒级，可以满足工程计算需求.

图3 初始截形配准Fig.3 Initial match between template curve and measured sectional points

图4 截形配准过程Fig.4 Different matching stages of template curve and measured sectional points

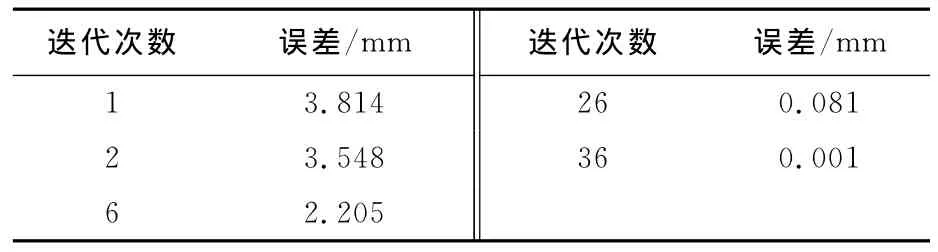
表1 不同迭代次数时与实际截形的误差Tab.1 Error with practical sectional points on different iterations

5 结 论

本文提出了基于变形模板的复杂截面轮廓重构模型和方法，相比于常规B样条曲线重构，其优势在于不必进行实测数据点的分割、序化和数据参数化.所提出的方法通过精确配准和模板变形迭代优化策略，有效避免了并行优化时的计算耗费过大等问题，并保证了模板在尽可能小的变形条件下实现与实际截形的贴合.采用的ICP精确配准模型和奇异值分解算法保证了配准的可靠性和精确性；单点和多点约束变形能够有效控制设计模板变形的趋势和幅值；提出的一种新的基于伯恩斯坦多项式算术运算和递归细分的最近点计算方法，能够克服经典迭代算法需要给定初始值且其精度依赖初始值的问题，计算精度高、速度快.下一步的工作是进一步将所提出的重构模型和方法应用于复杂曲面零件破损区域的几何修复中.

［1］Varady T，Martin R R，Cox J.Reverse engineering of geometric models－an introduction［J］.Computer－Aided Design，1997，29（4）：255－268.

［2］Weiss V，Andor L，Renner G，etal.Advanced surface fitting techniques ［J］.Computer Aided Geometric Design，2002，19（1）：19－42.

［3］LI Yong－qing，HUANG Xiao－ping，GONG Chenhe，etal.An engineering rule based parameterization approach for turbine blade reverse engineering ［C］／／ Proceedings of the Geometric Modeling and Processing.Beijing：IEEE Computer Society，2004：311－318.

［4］LI Yong－qing，HUANG Xiao－ping，GONG Chenhe，etal.Sketch template based parametric modeling in reverse engineering ［J］.Computer－Aided Design ＆ Applications，2005，2（1－4）：19－28.

［5］KE Ying－lin，ZHU Wei－dong，LIU feng－shan，etal.Constrained fitting for 2Dprofile－based reverse modeling［J］.CAD Computer Aided Design，2006，38（2）：101－114.

［6］XIE Hui， QIN Hong.A novel optimization approach to the effective computation of NURBS knots［J］.International Journal of Shape Modeling，2001，7（2）：199－227.

［7］ZHANG Cai－ming，HAN Hui－jian，Cheng F F.Determining knots by minimizing energy ［J］.Journal of Computer Science and Technology，2006，21（2）：261－264.

［8］LI Yong－qing，HUANG Xiao－ping，GONG Chenhe，etal.Sketch template based parametric modeling in reverse engineering ［J］.Computer－Aided Design ＆ Applications，2005，2（1－4）：19－28

［9］Besl P J，Mckay N D.A method for registration of 3－D shapes ［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1992，14（2）：239－256.

［10］Menq C，Yau H，Lai G.Automated precision measurement of surface profile in CAD－directed inspection［J］.IEEE Transactions on Robotics and Automation，1992，8（2）：268－278.

［11］Li Z，Gou J，Chu Y.Geometric algorithms for workpiece localization ［J］.IEEE Transactions on Robotics and Automation，1998，14（6）：864－878.

［12］Berchtold J，Bowyer A.Robust arithmetic for multivariate Bernstein－form polynomials ［J］.CAD Computer Aided Design，2000，32（11）：681－689.

［13］MA Ying－liang，Hewitt W T.Point inversion and projection for NURBS curve and surface：control polygon approach ［J］.Computer Aided Geometric Design，2003，20（2）：79－99.

［14］Arun K S，Huang T S，Blostein S D.Least－squares fitting of two 3－D point sets［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1987，9（5）：687－700.

［15］朱心雄.自由曲线曲面造型技术 ［M］.北京：科学出版社，2000.ZHU Xin－xiong.Free－form Curves／Surface Modeling Technology［M］.Beijing：Science Press，2000.（in Chinese）

［16］Hus W M，Hughes J F，Kaufman H.Direct manipulation of freeform deformation ［J］.Computer Graphics，1992，26（2）：177－184.