基于tanδ积分值的乙丙橡胶绝缘电缆含水量评估

周 长 亮， 王 志 强， 李 国 锋

（大连理工大学 电子信息与电气工程学部，辽宁 大连 116024）

0 引 言

在长期工作过程中，电缆的主绝缘材料由于受到潮湿、高温、振动、盐雾等因子的联合老化作用，其力学性能、电性能逐渐变坏，严重时会导致绝缘失效.绝缘材料中的含水量是影响电缆绝缘老化的重要因素之一.绝缘材料中含水量的增加，会使其绝缘性能下降、老化加速，从而导致绝缘的可靠性降低，寿命缩短.研究表明，每当含水量增加0.5%，绝缘材料的寿命就会缩短至原来的一半［1］.

乙丙橡胶（EPR）作为一种良好的绝缘材料，广泛应用于船用低压电缆.由于船舶的特殊敷设环境，如高湿度、高盐雾，含水量对电缆老化程度的影响就显得尤为重要.船舶电缆分为主干电缆和区域电缆［2］，其中主干电缆多为穿过耐压舱壁电缆，与船体同寿命.因此准确评估电缆的老化程度并研究影响其寿命的因素，对延长其使用寿命和安全运行有重要的意义.

对电缆绝缘材料含水量进行诊断的方法主要有称重法和卡尔滴定法，这两种方法都需要对试样进行取样，属于有损检测的范畴.但是对于在使用中的电缆是不允许对绝缘材料进行破坏的，所以这两种方法都无法应用于敷设中的电缆.因此本文预找寻一种基于电气参数的诊断方法.介电频谱测量是目前研究的热点之一，这种方法属于无损检测范畴，除了能诊断含水量以外还可避免电缆在测量过程中的损伤，达到诊断绝缘材料含水量的目的.

介电频谱测量分为时域测量和频域测量，在实际测量中，频域测量的一个重要参数测量就是介质损耗角正切值（tanδ）测量，即在改变输入信号频率的条件下测量介质损耗曲线.Nikolajevic研究了交联聚乙烯电缆和乙丙橡胶绝缘电缆绝缘材料在水分或水汽等老化应力作用下，介电频谱在1×10－3～1×103Hz的变化趋势［3］，认为含水量的增加直接导致材料tanδ的增加；Neimanis等采用介电频谱法研究了油纸绝缘材料中的含水量，认为含水量导致了响应曲线的偏移，并且在小于10Hz的频段偏移最明显［4］.上述文献仅对绝缘材料中的含水量与tanδ的关联性给出了定性的解释，没有给出定量的结果.

本文以乙丙橡胶绝缘电缆为实验对象，在固定的温度下对乙丙橡胶绝缘材料进行浸水加速热老化，分析不同含水量与tanδ之间的关联，对曲线进行积分运算后拟合出面积值与含水量的方程，同时在存在干扰因素下，测量不同老化程度的加热试样和浸水试样的tanδ曲线，得到双老化因素的物理模型并排除干扰因素对tanδ的影响，推导出定量计算的方程.最后证明利用1×10－2～1Hz频率范围内tanδ曲线的积分可关联乙丙橡胶绝缘电缆中含水量和老化程度的关系.

1 实验方法

1.1 电缆样品

电缆样品采用CEF／DA型0.6／1kV乙丙橡胶绝缘氯丁橡胶护套船用电力电缆，其结构如图1所示.电缆的线芯材料为铜，绝缘材料为乙丙橡胶，护套材料为氯丁橡胶.电缆的结构参数如表1所示.

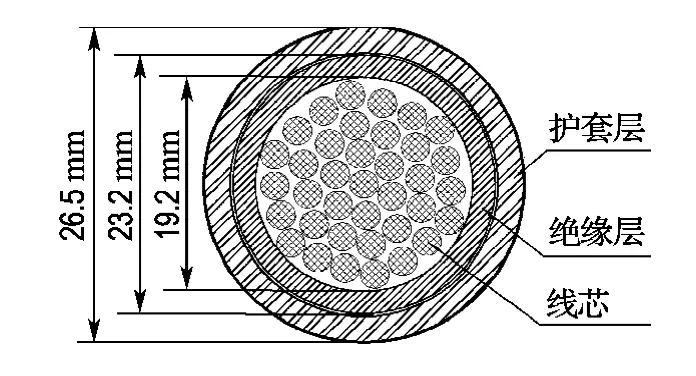
图1 乙丙橡胶绝缘电缆的结构Fig.1 The composition of EPR insulated cable

表1 实验中电缆试样的结构参数Tab.1 The structural parameters of cable specimen

1.2 电缆浸水加速热老化实验方法

由于船用电缆的特殊使用环境，对电缆样品采用海水浸泡实验.按照国际标准IEC 60811－1－1：2001中的规定制作哑铃试样，试样的尺寸如图2所示.将制备好的电缆试样分成2组：一组将试样浸泡在3%NaCl溶液（模拟渤海海域海水盐度）的1 000mL烧杯中，按规定时间取样分析；另一组将试样分别放入热老化烘箱和浸泡在3%NaCl溶液中，设定老化温度为90℃，进行正常的加速热老化实验.

老化实验一共进行32d，在此过程中，分别以下列时间节点进行取样：0、2、4、8、16、24、32d.每个时间点2个试样，试样至少浸泡24h后，取出并擦干表面水分，放置24h，然后进行橡胶吸水量测试和tanδ曲线测量.

图2 实验中哑铃试样的尺寸Fig.2 The dimension of dumbbell specimens in the laboratory

橡胶材料的吸水量测试和tanδ曲线测量按照IEC 60811－1－1：2001 执行.将整根电缆样品（长度10m）去除外护套层，两端头剥掉50mm的绝缘层，露出线芯，吊入水池中（水池中为3%NaCl溶液）并升温至90℃.水应浸没除电缆端头线芯部分的整根电缆，按照0、2、4、8、16、24、32d的时间节点，测试电缆绝缘层的tanδ.电缆端头接测试端，水箱为接地端.测试完成后切取100 mm长度绝缘层，擦干表面水分及堆积的盐分，放置24h，完成橡胶吸水量测试.

tanδ测试采用瑞典皇家科学院设计的“绝缘诊断系统IDA200”.通常测量信号源为140V正弦电压，在扫频范围1×10－3Hz到1×103Hz的情况下进行tanδ和电容（C）的曲线绘制.电介质的含水量一旦发生变化，其本身的电容、电阻率以及介电常数都会发生改变，材料的tanδ也随之变化［5］.反之，通过tanδ的测量也可以对介质绝缘材料的整体受潮状况进行判断.

2 实验结果及讨论

2.1 绝缘材料含水量的测定

在实验室内利用称重法测量实验中处理后试样的含水量.表2中列出了绝缘材料哑铃试样浸泡不同时间后的平均含水量w.乙丙橡胶材料中的含水量随着浸泡时间的增加而递增.其原因是乙丙橡胶在合成过程中混有数量很大的配合剂，其中有些配合剂单独存在时具有水溶性，因此随着浸水老化时间的增加，橡胶的含水量增加，实际反映的是一个缓慢的配合剂溶解过程.

实验中选择3%NaCl溶液作为浸泡溶液，其目的是提高饱和情况下绝缘材料内部的含水量.实验后期将试样放置24h，并仔细擦除了表面多余的盐分，完成含水量和电气参数的测量.文献［4］中利用tanδ在频率区间上的最小值来判定油纸绝缘材料的含水量，指出浸泡溶液的盐分不会对tanδ产生影响.由于水分与介质形成夹层极化，介质损耗主要表征绝缘材料的电导损耗和松弛损耗［6］.因此经过处理后的试样可以忽略盐分对tanδ的影响.

表2 乙丙橡胶绝缘哑铃试样在不同浸泡时间后的含水量平均测定值Tab.2 The average measured values of moisture contents of EPR insulated dumbbell specimens in different immersed aging time

由于在常温条件下，绝缘材料的老化过程十分缓慢，在此忽略因绝缘劣化程度所造成的测量误差.对于绝缘材料老化所造成的误差会在后面的实验中进一步分析讨论.

2.2 含水量对绝缘材料tanδ的影响

为了分析含水量对tanδ的影响，分别测量了不同含水量常温老化的乙丙橡胶绝缘材料的介电频谱响应曲线.介电频谱的测量频率范围从1×10－2Hz到1×103Hz，具体的测量曲线如图3所示.

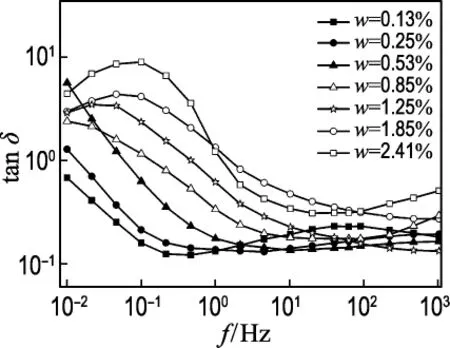
图3 乙丙橡胶绝缘材料不同含水量下的tanδ曲线图Fig.3 The tanδcurves of EPR insulation material with different moisture contents

从图3中可以看出tanδ曲线具有4个主要的趋势：（1）在含水量较低的情况下（0.13%～0.53%）在低频范围内存在最小值，含水量较高时（0.85%～1.85%）最小值在1×103Hz处；（2）含水量超过2%时曲线逐渐在低频处出现了最大值；（3）曲线的整体走势呈现出随含水量的增加而向高频方向移动；（4）含水量为2.41%的tanδ曲线呈现出异常的波动，并且在低频处曲线明显地分散.

绝缘材料中含有水分情况下的tanδ曲线整体规律是：当含水量较低时，tanδ曲线存在最小值，tanδ曲线出现最小值是由 Maxwell－Wagner效应引起的［5］；而当含水量增大到一定程度时，最小值在频率区间内消失；无论是最小值还是最大值都随着含水量的增加而向高频的方向横向移动，这种现象与文献［7］中论述的油纸绝缘材料的规律相似.由此可以看出，tanδ曲线最小值可以表征低含水量情况，而最大值可以表征较高含水量情况.但是，对于绝缘材料中含水量检测来说，利用tanδ曲线的最大值或最小值无法很好地判断含水量.

因此，针对上述tanδ曲线最值方法的不足，采用tanδ曲线的敏感区间分析方法，发现低频处的曲线特征与含水量情况比较吻合.图4中展示了在1×10－2～1Hz的tanδ曲线，发现tanδ具有较好的单调性规律.因此对该数据点进行曲线拟合，并在1×10－2～1Hz进行曲线积分计算，所围成的面积与含水量具有相似的单调性.不同含水量的乙丙橡胶绝缘材料tanδ积分计算后得到的面积值（x）见表3.

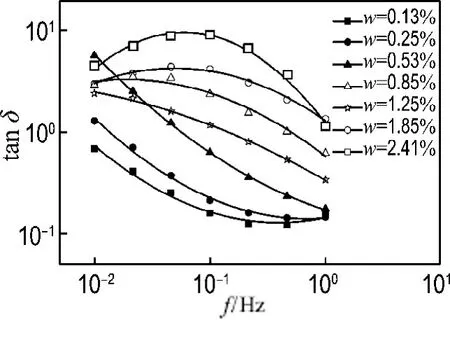
图4 绝缘材料在频率区间1×10－2～1Hz内tanδ拟合曲线Fig.4 The fitting curves of tanδat 1×10－2－1Hz on insulations

表3中离散数据的走势如图5所示.由此可见，数据具有下凹的增长趋势，初步判断与指数增长的公式形式是吻合的.同时，文献［4］和［8］中阐述了油纸绝缘材料的含水量与tanδ之间的关系，对增长趋势进行了公式拟合.根据离散数据特征和其他绝缘材料的含水量公式，对离散数据进行了曲线拟合，得到的1×10－2～1Hz内tanδ曲线积分值与含水量公式为

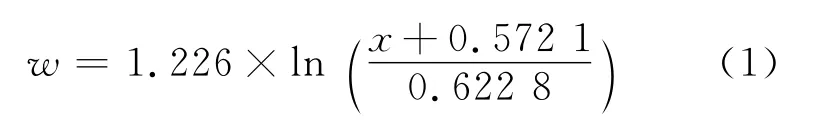
式中：w为含水量；x为tanδ曲线积分值.

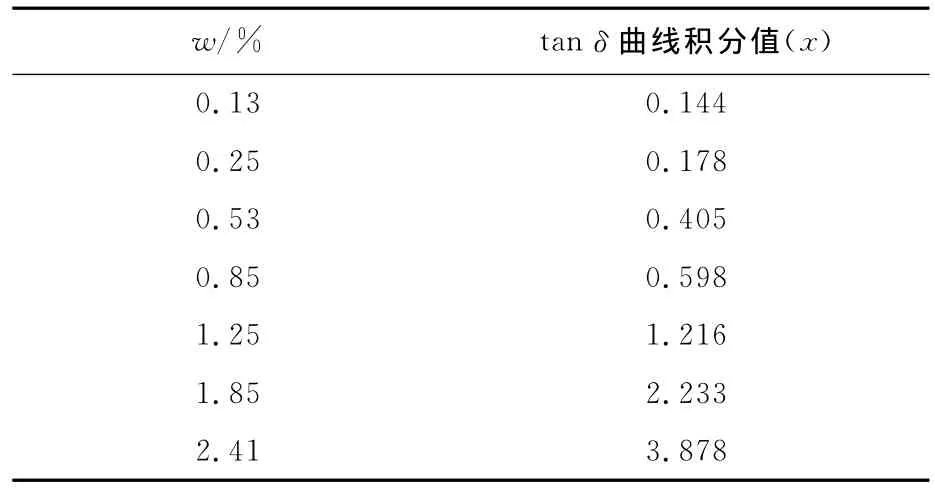
表3 浸水试样不同含水量所对应的tanδ曲线积分值Tab.3 The moisture contents of specimens and integral values of tanδ curves after water－immersed aging

拟合结果如图5所示，与离散数据吻合较好.因此在测量的含水量范围内，式（1）明确地反映了tanδ曲线积分值与含水量之间的关系.此时的分析只是在理想的条件下，还存在一些影响因素需要进行排除，或者是对含水量公式进行调整.

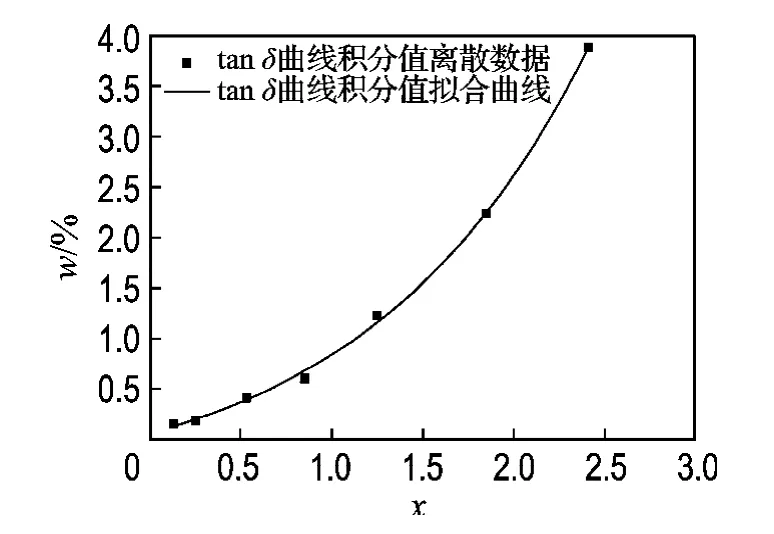
图5 tanδ曲线积分值与含水量之间的拟合曲线图Fig.5 The fitting curve between the integral values of tanδand moisture content

2.3 水分存在下电缆老化程度与tanδ的关系

高温是造成绝缘材料劣化的主要因素之一.因此，在绝缘材料的浸水加速热老化实验中，测量高温老化32d的干燥和浸水老化试样的tanδ曲线如图6和7所示.

由图6可以看出：高温加速老化造成了tanδ的增加，在低频范围内和特定的频率点表现出不同的特征值，其具体的对比结果如表4所示.主要原因是绝缘材料在老化过程中，材料发生了氧化降解反应而产生了损耗，导致tanδ的增加.

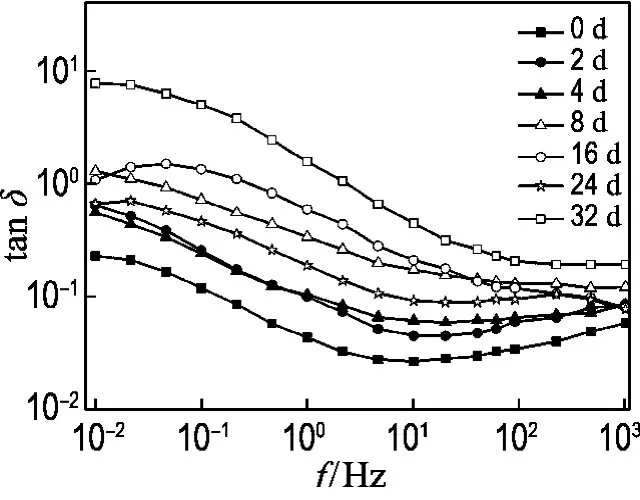
图6 干燥老化条件下绝缘材料的tanδ曲线Fig.6 The tanδcurves of insulations aged in dry condition

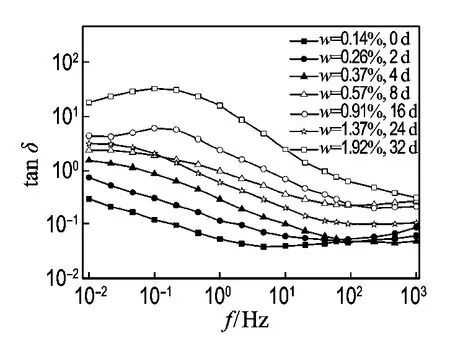
图7 浸水老化条件下绝缘材料的tanδ曲线Fig.7 The tanδcurves of insulations aged under water－immersed aging

表4 特定频率下干燥和浸水老化试样的tanδ的对比Tab.4 Comparison of tanδat special frequency after dry and water－immersed aging

由图7浸水条件下tanδ曲线可见：老化初期tanδ下降速度较快，后期的变化程度明显变缓，其主要原因是在橡胶合成过程中，有多种添加剂成分具有溶水性和内部具有杂质或者气泡的存在.环境中的水蒸气和氧扩散、渗入天然橡胶硫化胶内部，引起内部添加剂的溶解并使内部产生裂纹，同时伴随有孔洞产生；在有氧气渗入的情况下引起天然橡胶硫化胶的氧化降解，加速了天然橡胶老化失效.当多条裂纹会聚于添加剂颗粒时，添加剂颗粒脱离原来位置，产生孔洞，从而使材料内部发生极化现象，造成tanδ的增加或者是曲线的变化［9］.

对比图6和7，水分造成的tanδ的差值见表5，其中选择了曲线图中的参考点分别为50Hz的tanδ值和1×10－2～1Hz的tanδ积分值.定量分析绝缘材料在浸水加速热老化条件下的tanδ曲线，可得出含水量对tanδ的影响.

从表5中可以看出，加入水分因素老化后的tanδ较单因素的值要大，由于在多因素共同老化作用下，乙丙橡胶绝缘材料受到热和水分的共同作用，其失效时间明显地短于两种单因素的单独作用.对于这种共同作用的效果，有学者推导出了电缆的多种老化模型［10］.

本文结合相应的模型和前面单独水分的影响因素来总结特征方程.对tanδ积分数据进行拟合，由方程（1）变形推出tanδ与含水量的关系为

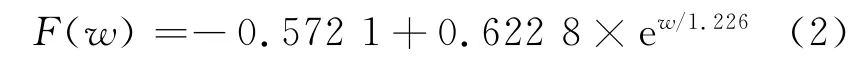
将高温下的含水量进行tanδ的换算.同时，干燥条件与高温浸水条件下存在的差值，与含水量的换算结果相比是不等价的，可见老化因素之间是互相影响的，存在一个影响函数f（T，w）.

表5 高温浸水试样的tanδ与含水量换算结果及差值Tab.5 The conversion results between tanδand moisture content and errors of samples under thermal and water－immersed aging

因此，根据传统的经验模型中绝缘材料的热－电联合老化模型［11］，不妨假设多因素的老化方程为

式中：lgτ为绝缘材料老化时间；T（δ）为温度对老化时间的影响函数，符合Arrhenius方程；F（w）为老化因素水分对材料老化时间的影响函数；f（T，w）为老化因素水分与老化因素温度之间的影响函数.

式（3）中的F（w）函数形式如式（2）所示，T（δ）的表达形式在前期研究工作中给出了明确的推导［12］.函数基本上符合Arrhenius方程的表达形式，其中老化常数可参考失效的标准，使用最小二乘法计算得到.

参考前面经过实验数据拟合出的含水量与tanδ之间的关系方程，从中可以发现测量值偏大的部分明显大于单一因素逐一影响，从而得出f（T，w）函数的表现形式，如下式：

将式（4）代入多因素老化方程（3）中，从而可以通过tanδ积分值的测量并结合电缆绝缘材料的实际使用情况，推导出绝缘材料中的含水量，排除了温度对tanδ的影响.

归根结底，由于高温加速了绝缘材料的劣化，引起tanδ的增加和曲线规律性的变化，通过排除寿命方程中老化因素对tanδ的影响，进而可推导出绝缘材料内部的含水量情况.

3 结 论

在不同含水量情况下，研究了乙丙橡胶绝缘介质损耗频谱曲线的变化规律，发现介质损耗频谱曲线在1×10－2～1Hz对老化情况较为敏感，采用曲线积分的测定方法发现测量值与含水量呈现指数形式的变化规律.利用浸水条件下的实验结果推导出了tanδ曲线的积分值与含水量之间的关系方程，得到了常温下含水量的测定公式.

考虑实验中主要受到温度因素影响，在高温浸水老化实验下，修正tanδ曲线的积分值后得到归一化的方程及多因素相互影响函数，获得绝缘材料多因素老化方程.排除掉温度所造成tanδ的增加，从而可利用前面推导出的含水量方程来判定绝缘材料内部含水量.因此，可以利用测量乙丙橡胶绝缘材料的tanδ在1×10－2～1Hz的积分值来测定其含水量.

［1］Gillen K T，Bernstein R，Clough R L，etal.Lifetime predictions for semi－crystalline cable insulation materials I：Mechanical properties and oxygen consumption measurements on EPRmaterials ［J］.Polymer Degradation and Stability，2006，91（9）：2146－2156.

［2］Gubanski S M，Boss P，Csepes G，etal.Dielectric response methods for diagnostics of power transformers ［J］.IEEE Electrical Insulation Magazine，2003，19（3）：12－18.

［3］Nikolajevic S V.The behaviour of water in XLPE and EPR cables and its influence on the electric characteristics of insulation ［J］.IEEE Transations on Power Delivery，1999，14（1）：39－45.

［4］Neimanis R，Eriksson R.Diagnosis of moisture in oil／paper distribution cables－Part I：Estimation of moisture content using frequency－domain spectroscopy ［J］.IEEE Transactions on Power Delivery，2004，19（1）：9－14.

［5］Nettelblad B.Effect of moisture content on the dielectric properties of cellulose［C］／／Proceedings of the Nordic Insulation Symposium NORD－IS′92.Sweden：ABB Corporate Research Press，1992：8－9.

［6］Jagadeesh K V，Sankaran P，Sudhakar R K.Measurement ofCand tanδof a capacitor employing PSDs and dual－slope DVMs ［J］.IEEE Transactions on Instrumentation and Measurement，2003，52（5）：1588－1592.

［7］Jonscher A K.Dielectric Relaxation in Solids［M］.London：Chelsea Dielectric Press，1983.

［8］Neimanis R，Eriksson R，Papazyan R.Diagnosis of moisture in oil／paper distribution cables －Part II：water penetration in cable insulation－experiment and modeling［J］.IEEE Transactions on Power Delivery，2004，19（1）：15－20.

［9］Hsu Y T，Chang－liao K S，Wang T K，etal.Monitoring the moisture－related degradation of ethylene propylene rubber cable by electrical and SEM methods ［J］.Polymer Degradation and Stability，2006，91（10）：2357－2364.

［10］Gjarde A C.Mutifactor ageing models－origin and similarities ［J］.IEEE Electrical Insulation Magazine，1997，13（1）：6－13.

［11］Montanari G，Mazzanti G，Simoni L.Progress in electro－thermal life modeling of electrical insulation during the last decades ［J］.Dielectrics and Electrical Insulation，2002（10）：730－745.

［12］ZHOU Chang－liang，WANG Zhi－qiang，LI Guofeng.Application of low frequency dielectric spectroscopy to estimate lifetime of low－voltage EPR insulation ［J］.Journal of Convergence Information Technology，2012，7（8）：44－53.