连铸坯液固相分数检测及液芯末端位置定位新方法

王兆峰， 姚 曼， 王旭东＊， 李国斌， 刘 宇， 施桂钱， 杨龙胜， 陆洪周， 张晓兵

（1.大连理工大学 电子信息与电气工程学部，辽宁大连 116024；2.大连理工大学 材料科学与工程学院，辽宁大连 116024；3.江苏沙钢集团，江苏 张家港 215625）

0 引 言

连铸生产中，钢液在结晶器内部受到强烈冷却作用形成具有一定厚度和强度的坯壳.进入二冷区后坯壳厚度不断增加，铸坯内部液芯逐渐减小，直至液相分数为零时，铸坯液芯完全凝固，铸坯即完成由液相转变为固相.如能对生产中铸坯的液固相分数进行准确测量，尤其是对铸坯凝固末端位置的精确预报，对生产无内部缺陷铸坯和实现动态轻压下工艺具有重要的现实意义.凝固末端不仅是铸机设计和制定连铸工艺的主要依据，也是连铸过程控制、改善铸坯内部组织，以及提高铸坯质量与生产效率的重要参数［1－3］.

作为改善铸坯内部质量的重要手段，轻压下和凝固末端电磁搅拌技术在近年来取得了长足进步.其中，压下效果与压下（或电磁场施加）位置密切相关，而适当的压下位置又决定于铸坯内部的液固相分数［4］.生产实践表明，铸坯液固相分数的准确获取对于轻压下工艺的实施有着重要的指导作用.

目前，关于铸坯凝固末端位置的确定方法主要包括实验测量、数值模拟和测力传感器探测3种方法.实验测量法包括射钉实验、坯壳穿刺、同位素示踪等，这些方法多采用破坏性实验，可以针对少数样本试样进行研究，不适用于大规模的工业生产.数值模拟则通过传热控制方程，模拟铸坯在结晶器与二冷区的传热与凝固过程，获得铸坯的液相、固相分数及凝固终点的位置［5－8］，由于建立模型时引入了诸多简化和假设，计算结果难免与实际有一定偏差.赵志毅等［9］通过在扇形段某处安装测力传感器检测反馈信号来确定凝固末端的位置.这种方法要对扇形段进行上框架和下框架的硬件改造，对设备结构改动较大.

针对上述问题，本文采用理论解析、物理模拟和实验验证等方法，尝试开发连铸坯液固相分数及液芯末端位置检测的新方法，并对检测方案总体思路的可行性进行论证，为其在线应用提供指导和参考.

1 固液共存条件下受迫振动模型

图1（a）为连铸坯凝固末端轻压下过程的示意图；图1（b）为二冷区铸坯横断面，在该处铸坯尚未完全凝固，处于液固共存状态.以图1（a）中的B位置处一段铸坯为研究对象，对其施加一定振频和幅度的正弦振动激励，则其在受迫振动的任一瞬间，以平衡位置为坐标原点，垂直方向向下为正，作用在B上的力如图2所示.其中Fi（t）为惯性力，Fi（t）＝－mx··（t）；Fc（t）为阻尼 力，Fc（t）＝－cx·（t）；Fe（t）为弹性力，Fe（t）＝－kx（t）；激振力Fp（t）是按正弦函数变化的周期荷载.根据图2的受力分析，由达朗伯原理和杜哈梅积分可导出其振动微分方程，如式（1）和（2）：

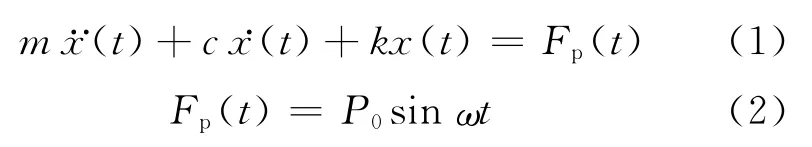
式中：m为振动单元质量，kg；x（t）为振动单元位移，m；t为时间，s；c为黏滞阻尼系数，N／m·s－1；k为系统刚度，N／m；ω为激振力的激振频率，rad／s；Fp（t）为激振力，N；P0为激振力的最大幅值，N.

图1 连铸坯凝固末端轻压下示意图及铸坯横断面Fig.1 Schematic view of final solidifying end and cross section of slabs under soft reduction

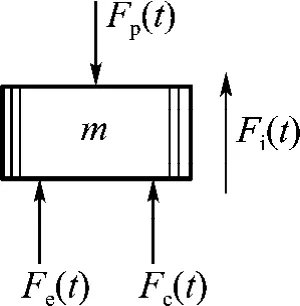
图2 振动单元的受力分析Fig.2 Force analysis of vibrating particle

这里x0为有阻尼纯受迫振动下振动单元位移的幅值，φ为位移与激振力之间的相位差.

设外力在一个振动周期内对系统做的功为Wp，则微功

进而

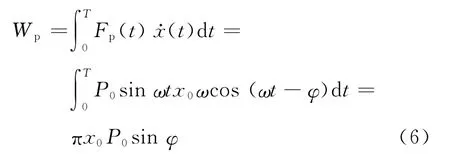
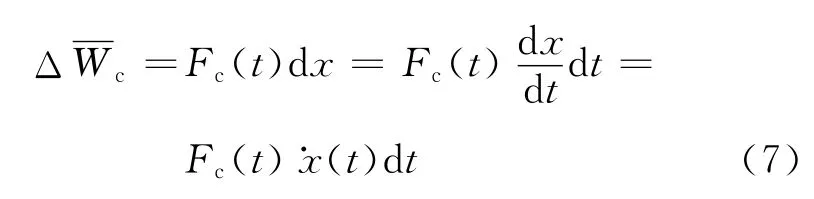
那么阻尼力在一个振动周期内消耗的能量，设为Wc，可表示为

假如系统没有阻尼，力和位移的相位差φ＝0或φ＝π，这时Wp＝0.若φ≠0且φ≠π，则此功消耗于阻尼，即Wp＝Wc，可得

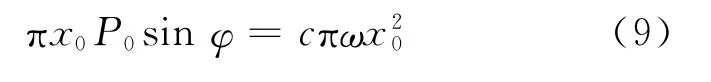
这里c＝2mωnξ，由此得出

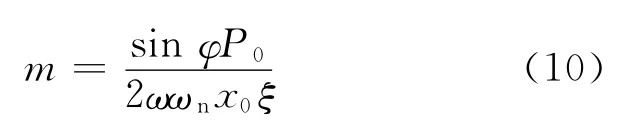
在连铸坯凝固过程中，铸坯在不同拉速、浇铸温度等工艺条件下，其横断面液固相分数沿浇铸方向不断变化，其质量应是液相分数的函数，即m＝f（fl）（这里fl表示液相分数）.由于固相分数fs＝1－fl，忽略温度对液、固相密度的影响，m与fl间存在线性反比关系.

若液芯未完全凝固，即fl＞0，则外力受迫振动条件下，液固共存时液体振动消耗的阻尼功即为Wc，同时φ≠0且φ≠π.令θ＝ω／2π，结合式（10）可推出

其中K是铸坯液芯及固态坯壳密度相关的修正系数.在一定的受迫振动条件下，上式中的θ、P0为已知量，因此在理论上，若能在线确定x0、φ、ωn和ξ，即可求出二冷区特定位置的液相及固相分数.

2 实验描述

2.1 物理模型的建立

针对连铸过程的实际工况，本文从相似理论出发，建立了一套铸坯液固相分数检测系统的物理模拟装置.建立物理模型，须保证模型与原型之间的物理相似［10］.钢液在二冷区的凝固过程一般可视为黏性不可压缩且稳态的，可忽略化学反应的影响.为保证物理模型和实际铸坯在凝固末端原型相似，设计模型时需满足几何相似和动力学相似.几何相似即保证物理模型和铸坯原型各对应长度之比为一常数；动力学相似也就是系统内力的相似，模型和原型中各对应位置力的方向一致，大小成一定比例.本文中，采用有机玻璃来模拟已凝固的铸坯，内部用水来模拟尚未凝固的液芯部分.模型尺寸取为1 000mm×240mm×90 mm.除了满足几何相似和动力学相似外，还考虑到有机玻璃的密度（1.19×103kg／m3）稍大于水的密度，同实际过程中固态钢的密度略大于液态钢的密度相符合［11］.实验室模型装置示意图如图3所示.

图3 固液共存受迫振动物理模拟装置Fig.3 Physical simulation device of solid－liquid coexistence with forced vibration

2.2 实验方法

实验室建立物理模拟装置，模拟连铸坯在二冷区某一位置横断面上的固相与液相分布情况.如图3所示，通过改变系统内部有机玻璃板的形状和厚度，达到模拟不同液相分数的目的.外部激振器按照设定的振幅和振频，以正弦曲线方式对模型施加受迫振动.此外，通过安装测力传感器和位移传感器，检测装置振动过程中受力和振动位移的变化情况.实际生产过程中，考虑到铸机扇形段的结构特点，驱动辊与铸坯之间属于线接触，因此本文的实验中振动荷载也是以线接触的方式作用在模型装置上的.

按预先的设定量改变激振频率和激振力的大小，来观察不同激励条件下检测信号相位差的变化情况.按照有机玻璃和水的密度，实验中液相分数分别取为0.1、0.3、0.4和0.7，激振频率分别取3、4和5Hz，激振力分别取7、8和9N.

2.3 实验结果与分析

2.3.1 振动系统受力及位移的周期变化 实验过程中，装置在周期应力作用下，受激励而产生周期性振动.之后如继续施加周期性应力，试样便进行受迫振动.振动达到稳态以后，试样按照外加周期性应力的频率而振动，由于液相在振动时内部摩擦引起的机械振动损耗能量，即内部阻尼的存在，使得其周期应变的相位滞后于周期应力的相位，产生相位差［12－13］.图4给出了不同液相分数条件下模型装置的受力及反馈位移情况.

图4 不同液相分数下模型装置振动行为分析Fig.4 Vibration behavior analysis of model device with different liquid fractions

图4 中τ为应变波形滞后应力波形的时间；T为振动周期，相位差可以表示为

为便于比较，这里对外部施加的激振力取相同的振频和振幅.可以看出，液相分数为0.4的情况下应力和应变两路信号得到的相位差，明显大于液相分数为0.1的情况.实际的连铸过程中，铸坯的液相部分会随着外部冷却条件的施加和内部热量的散失而逐渐减少，坯壳不断增厚，直至完全凝固.当铸坯的液相分数较大时，阻尼效应亦较大，即位移相比于激振力相位的滞后程度增加，采集到位移和力两路信号的相位差增大.因此，根据如上实验结果，可以通过相位差的变化来追踪反映系统内部液相分数的真实情况.

2.3.2 振频对相位差的影响 首先保持外部激振力的大小恒定，逐步改变激振频率，考察相位差随液相分数的变化情况.这里以取激振力的大小为7N时的实验条件为例，不同激振频率下检测到的相位差随液相分数的变化情况如图5所示.

图5 不同激振频率θ下相位差随液相分数的变化情况Fig.5 Variation of the phase difference as function of the liquid fraction for different exciting frequencyθ

由实测结果可知，对于同一液相分数下的检测对象，随着激振频率的增大，相位差沿负向逐渐增大，位移滞后于激振力的现象愈发明显，这与频响函数伯德图中的相频特性曲线中的频率－相位变化规律是一致的；而在相同激振频率下，随着液相分数的增加，系统内部阻尼加大，周期应变的相位滞后于周期应力的相位情形加剧，所以相位差将有沿负向上升的趋势.

2.3.3 激振力对相位差的影响 在外部激振频率恒定的情况下，逐一改变激振力的大小，来观测相位差随液相分数的变化情况.以外部激振频率为4Hz的实验条件为例，所得到的相位差随液相分数的变化情况如图6所示.

可见，在外部激振频率恒定的情况下，相同液相分数下检测到的相位差随着激振力的变化波动不大，近似不变（见图6（a））.激振力大小的改变会影响反馈位移的变化（见图6（b）），而与相位差的变化无关.分析其原因：相位差主要由检测对象内部的阻尼效应决定，在其内部液固分布状态无变化时，相位差决定于位移和激振力二者通过振动基准位置（“振动零点”）的时序间隔，而与激振力的大小无关.激振力对振动系统的影响，则主要体现在振动位移能够达到的最大幅值.因此，随着液相分数的增大，位移滞后激振力的程度增加，相位差沿负向上升，见图6（a）.

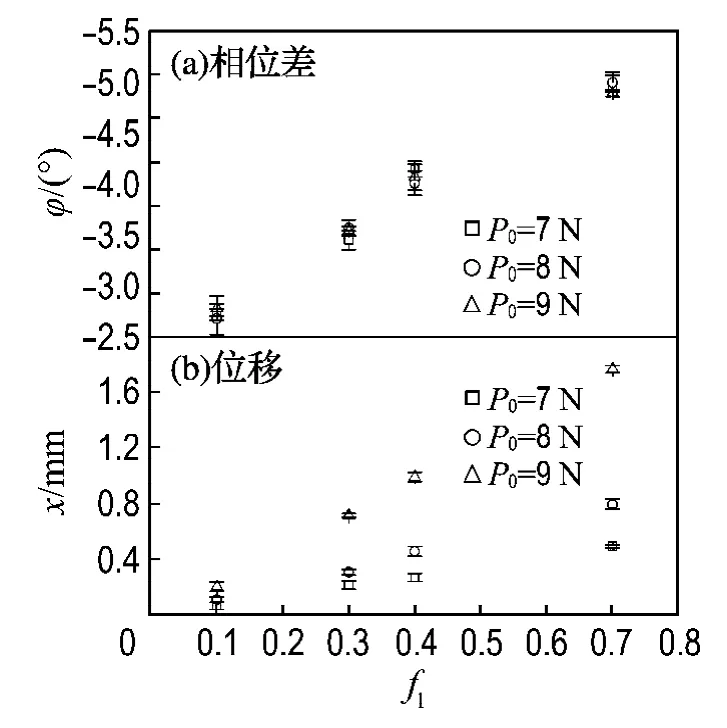
图6 不同激振力P0下相位差和反馈位移随液相分数的变化情况Fig.6 Variation of the phase difference and feedback displacement as function of the liquid fraction under different exciting force P0

3 理论解析与物理模拟的对比验证

联合上文理论推导及物理模拟实验，将两部分结果进行对比，以验证方法的合理性和可行性.

典型结构体系的真实阻尼特性是很复杂和难于确定的，因而通常采用自由振动条件下具有相同衰减率的等效黏滞阻尼比ξ来表示实际结构的阻尼［14］.本实验过程中采用自由振动衰减法来检测不同液相分数下的阻尼比ξ，同时物理模拟装置的ωn则可由共振时的相位判别法来确定［15］，并结合实验装置确定修正系数K.将ξ、ωn和K及两路传感器采集到的数据代入式（11），得到理论模型计算结果与实验值对比情况.图7（a）、（b）和（c）显示在振动频率分别为3、4和5Hz条件下，由建立的数学模型计算的液相分数值和物理模拟实验中采用的液相分数值吻合良好，验证了数学模型的正确性和准确性，为该方法和数学模拟应用于实际连铸生产过程，提供了理论基础和物理实验验证的支持.

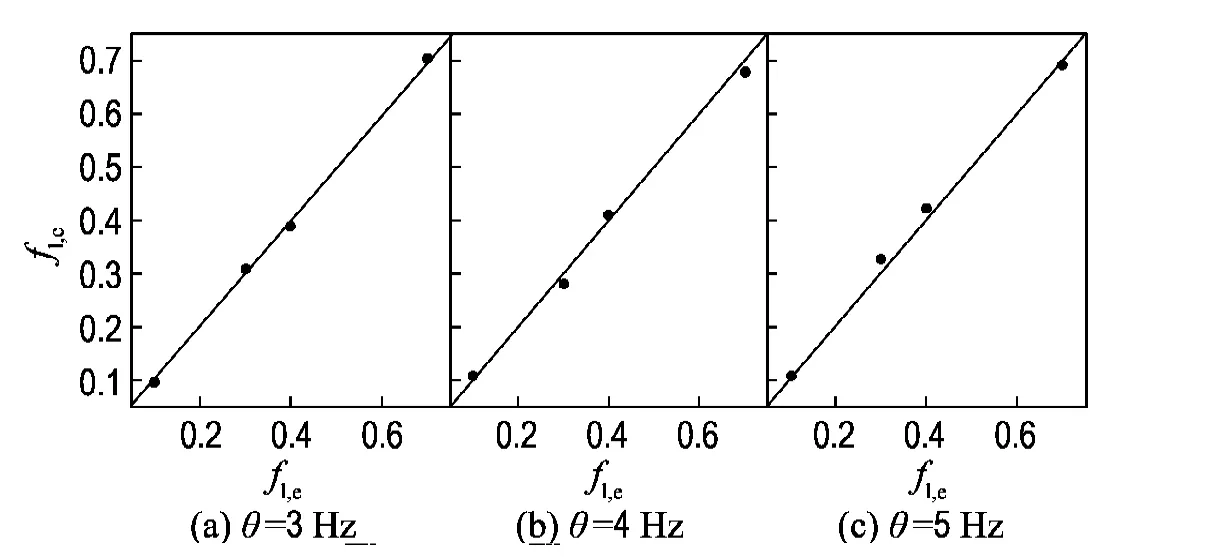
图7 液相分数的模型计算值fl，c与实验值fl，e对比Fig.7 Contrast of calculation results fl，cof the model and experimental values fl，efor liquid fractions

因此，根据上述检测方法，若能在实际的连铸生产中大致确定出铸坯凝固末端的区域，通过扇形段驱动辊于特定位置在铸坯表面施加一定频率和幅度的周期受迫振动，在不干扰生产过程和确保铸坯质量的前提下，对该区域内的铸坯施加一定频率和幅值的周期激振，借助振动在液相、固相中的阻尼衰减效应，可实时探测铸坯的凝固进程.对于一定的受迫振动条件，即确定了激振频率θ和幅值P0，同时在线测量反馈位移的幅值x0、两路信号的相位差φ，而铸坯的固有频率ωn和阻尼比ξ采用前文所述的方法加以确定，则可根据式（11）求出生产线中特定位置处的液固相分数.根据图5和6的实验结果，若铸坯已完全凝固，此时铸坯内部已无液相，则位移和力的相位差趋于零，则根据检测结果可确定铸坯完全凝固的准确位置.

4 结 论

本文提出了振动法检测连铸坯液固相分数和液芯末端位置的新方法.通过扇形段驱动辊在铸坯表面施加一定频率和幅度的周期受迫振动，借助振动在液相、固相中不同的阻尼衰减效应，根据激振力和受迫振动位移等信号反馈的规律性差异，实时探测铸坯的凝固进程，达到精确预报连铸坯液固相分数及凝固终点位置的目的.

理论解析、物理模拟和实验验证研究结果表明，受迫振动位移与激振力的相位差和液固相分数存在明确的对应关系，随液相分数增加，振动位移滞后于激振力的趋势加剧，二者相位差逐渐增大，经理论推导出的数学模型计算结果与物理模拟实验结果吻合，证实了检测方案的可行性.研究结果对于连铸轻压下、电磁搅拌工艺的制定和优化具有积极的指导意义.

［1］Samoilovich Y A.Effect of soft reduction on the structure of continuously－cast slabs ［J］.Metallurgist，2009，53（1－2）：98－104.

［2］Takahashi T，Ohsasa K I，Katayama N.Simulation for progress of solid－liquid coexisting zone in continuous casting of carbon steels ［J］.Tetsu－to－Hagane，1990，76（5）：728－734.

［3］Heinz H，Manfred T，Michael S，etal.Advanced equipment for high－performance caster ［J］.MPT International，2003，26（3）：74－79.

［4］Bleck W，Wang W J，Butle R.Influence of soft reduction on internal quality of high carbon steel billets ［J］.Steel Research International，2006，77（7）：485－491.

［5］Petrus B，Zheng K，Zhou X，etal.Real－time，model－based spray－cooling control system for steel continuous casting ［J］.Metallurgical and Materials Transactions B，2011，42（1）：87－103.

［6］Alizadeh M，Jahromi S A J，Nasihatkon S B.Applying finite point method in solidification modeling during continuous casting process ［J］.ISIJ International，2010，50（3）：411－417.

［7］仇圣桃，刘和平，干 勇.基于连续模型的板坯连铸凝固过程的数值模拟［J］.钢铁研究学报，2003，15（6）：16－20.QIU Sheng－tao， LIU He－ping， GAN Yong.Numerical simulation of solidification process of slab casting based on continuum model［J］.Journal of Iron and Steel Research，2003，15（6）：16－20.（in Chinese）

［8］郭 薇，祭 程，赵 琦，等.板坯连铸动态轻压下系统中在线实时温度场的计算模型［J］.材料科学与冶金学报，2006，5（3）：186－189.GUO Wei，JI Cheng，ZHAO Qi，etal.Study on online real－time temperature field calculation model for slab caster in the system of dynamic soft reduction［J］.Journal of Materials and Metallurgy，2006，5（3）：186－189.（in Chinese）

［9］赵志毅，康永林，刘德民，等.连铸板坯凝固末端在线监测系统 ［J］.北京科技大学学报，2003，25（5）：458－461.ZHAO Zhi－yi， KANG Yong－lin，LIU De－min，etal.Liquid core on－line detecting system on a slab continuous casting machine ［J］.Journal of University of Science and Technology Beijing，2003，25（5）：458－461.（in Chinese）

［10］朱苗勇，萧泽强.钢的精炼过程数学物理模拟［M］.北京：冶金工业出版社，1998.ZHU Miao－yong，XIAO Ze－qiang.Mathematical and Physical Simulation on Steel Refining Process［M］.Beijing：Metallurgical Industry Press，1998.（in Chinese）

［11］Burghardt A J C，Carless S P，Kamperman A A，etal.The formation of transverse depressions during casting studied by finite－element calculations［C］／／4thInternational Conference on Modelling and Simulation of Metallurgical Processes in Steelmaking.Düsseldorf：Steel Institute VDEh，2011.

［12］温金鹏，杨智春，李 斌，等.材料阻尼测试方法研究［J］.振动、测试与诊断，2008，28（3）：220－224.WEN Jin－peng，YANG Zhi－chun，LI Bin，etal.A method for material damping measurement ［J］.Journal of Vibration，Measurement ＆ Diagnosis，2008，28（3）：220－224.（in Chinese）

［13］张忠明，刘宏昭，王锦程，等.材料阻尼及阻尼材料的研究进展［J］.功能材料，2001，32（3）：227－230.ZHANG Zhong－ming，LIU Hong－zhao， WANG Jin－cheng，etal.Damping of materials and progress in the damping materials［J］.Journal of Functional Materials，2001，32（3）：227－230.（in Chinese）

［14］克拉夫 R W，彭津J.结构动力学［M］.2版.北京：高等教育出版社，2006.Clough R W，Penzien J.Dynamics of Structures［M］.2nd ed.Beijing：Higher Education Press，2006.（in Chinese）

［15］刘习军，贾启芬.工程振动理论与测试技术［M］.北京：高等教育出版社，2004.LIU Xi－jun，JIA Qi－fen.Engineering Vibration Theory and Testing Techniques［M］.Beijing：Higher Education Press，2004.（in Chinese）