基于键合图结型结构的矩阵变换建模法解析
2013-09-27田树军,胡全义,张宏*,高艳明
田 树 军, 胡 全 义, 张 宏*, 高 艳 明
(大连理工大学 机械工程学院,辽宁 大连 116024)
0 引 言
键合图结型结构(junction structure)的概念,是由对功率键合图理论与方法的发展作出重要贡献的Rosenberg于1971年首次提出的,并据此研发出从键合图模型出发,实现由计算机通过矩阵变换操作建立系统状态方程的自动建模程序ENPORT[1].这种矩阵变换建模方法在系统动力学研究领域具有较大的影响,其核心理念及建模推理规则对后续的自动建模软件开发具有独特的促进作用.
本文将对键合图结型结构的概念[2]作简要介绍,并着重对矩阵变换建模方法的要点及其适用条件等进行较深入的解析,以利于相关研究的借鉴和应用.
1 能量场与结型结构的基本概念
键合图中的功率键可分为内部键和外部键两类:凡与作用元相连接的键称之为外部键,而在结点及转换器、旋转器之间起连接作用的键称之为内部键.
如图1所示,对于内部键,所连接的是0结点、1结点、转换器TF和旋转器GY这4种连接对象的集合,该集合即为键合图的结型结构.
对于外部键,所连接的是各作用元,即容性元C、感性元I、阻性元R、流源Sf和力源Se.这5种作用元的功能又分为3类:容性元C、感性元I起储能作用,统称为储能元;阻性元R起耗能作用,故又称之为耗能元;流源Sf和力源Se则为外界的能量输入,统称之为源.根据这5种3类作用元各自的能量属性,将其归结为不同的能量作用场,简称为能量场或场.其中,储能元的集合称之为储能场,耗能元的集合称之为耗能场,而流源Sf和力源Se的集合则称之为源场.依据场的概念,任一能量系统,均可视为相互连接起来的各类能量场的集合.
图1为基于能量场概念的系统构成.
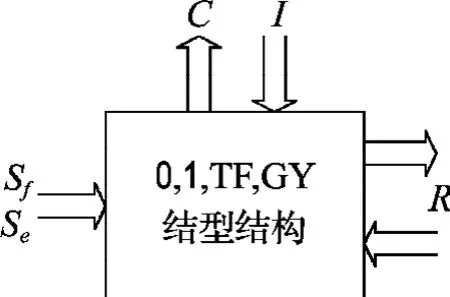
图1 能量场与系统构成Fig.1 Energy fields and systems composition
通过引入能量场和结型结构的概念,在应用功率键合图作为建模工具进行动态模型设计时,有以下两点鲜明的作用和意义:其一,便于研究分析人员站在更高的层面,全面、清晰地审视和了解所研究系统的动态结构,准确把握各种动态影响因素的特征及属性,正确处理建模过程中所遇到的各类相关问题;其二,便于规范和理顺系统中各种功率变量的关系,明确相关数学描述形式(诸如各功能矩阵)的特征和属性,以在键合图相关规则的基础上,更为顺畅有序地推导建立起系统数学模型——状态方程.
2 场方程、结型结构方程和系统状态方程[3-4]
2.1 场方程
场方程是用来描述结型结构向能量场的输入向(变)量与场的输出向(变)量之间关系的方程.场方程所涉及的系统变量,除键合图的基本变量流变量f和力变量e外,还有如下其他变量.
(1)能量变量X
能量变量X是指结型结构(结点)通过储能键向储能元C或I输入的相应流变量f或力变量e的积分.通常,若不考虑建模中较少出现的机械旋转运动和电能量,则可认为能量变量X为如下元素的集合:液体体积运动件位移运动件动量液体动量.故此,能量变量X又可表示为X
(2)共能变量Z
共能变量Z是指在储能键上,储能元C或I作用并输出给结型结构(结点)的相应流变量f或力变量e.之所以称之为共能变量,是因为这种变量的量值一经从储能元反馈输出到结点,则被结点周围其他各键上相同属性的变量所共有.
基于和能量变量X同样的考虑,则共能变量Z可认为是如下元素的集合:液体压力p,p=运动件弹性力运动件速度液体流量q,q=
(3)耗能场的输入变量Din和输出变量Dout
由于耗能键所连接的阻性作用元R在因果关系设定上具有自由性,耗能键上的两个功率分量即流变量f和力变量e,均有可能作为对阻性元R的输入变量和由R反馈回结点的输出变量.分别记输入变量为Din,输出变量为Dout.
基于上述定义和分析,若系统是线性的且不存在微分因果关系,可建立如下储能场方程:

及耗能场方程:

式中:S、L均为方阵.
2.2 结型结构方程
能量变量X一般如前所述地表现为液体体积V、运动件位移x、运动件动量P和液体动量Ph这4种元素的集合;而这4种元素又以积分表达式的形式与相对应的流变量或力变量相联系着.事实上,积分式可以等效地变换成微分表达式的形式,即
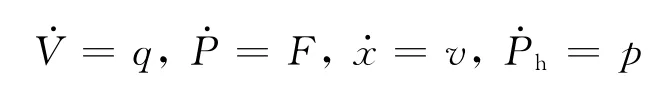
由于各微分式右端的变量都是对于储能作用元的输入变量,则左端各导数项也同样是其输入变量.通过由积分表达式向微分表达式的等效变换,将为系统状态方程的建立奠定基础和提供便利.按照归一化表达方式,上述各式左端的导数项均可归结为能量变量X对时间t的导数,而各式的右端变量即液体流量q、作用力F、运动件速度v和液体压力p均可归结为相应的流变量f和力变量e.
表1给出了各类能量场的输入和输出变量.
不难看出,在系统动态过程中的任一时刻,能量场所接受的来自结型结构的输入变量,就是表征系统在该时刻状态的特征变量;而能量场对结型结构的输出变量,则可视为是该时刻结型结构所受到的激励,且正是这些激励性变量的激励作用,将引起结型结构即系统新的状态变化.

表1 各类能量场的输入、输出变量Tab.1 Input and output variables for different energy fields
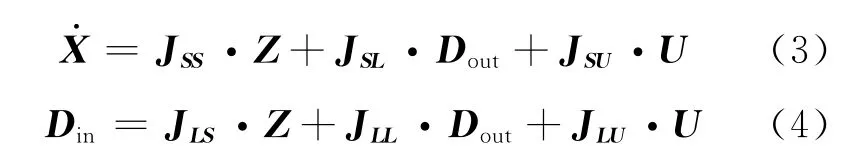
式(3)、(4)中的各关联矩阵J表征了各能量通口对于相应输入输出变量所具有的关联制约作用,且各J中的非零元素均与相应通口的属性参数相对应.关联矩阵J还具有一些数学上的特征和性质,如矩阵JSS和JLL(如果它存在)为反对称矩阵,而JSL和JLS则是互为负转置的矩阵.这些数学性质对于建模尤其是自动建模过程中实施检查和判断,以避免本质性错误的发生,具有其独特的作用.
2.3 系统状态方程
结型结构方程(3)已经构成了状态方程的雏形.对比线性系统状态方程的基本形式BU可知,后续的工作将是如何消去式中作为中间变量的Dout;而要做到这一点,只需借助储能场方程(1)、耗能场方程(2)和结型结构方程(4),实施必要的矩阵变换和等量代换,即可完成.这也就是矩阵变换建模法得名的由来.
经一系列矩阵变换,最后得

令

及
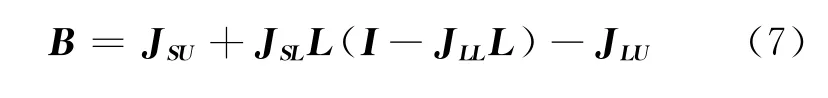
于是,得到系统状态方程的最终通用形式:
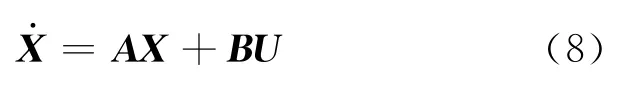
3 关于矩阵变换建模法适用性的分析
(1)对于线性定常系统,且在无非标准型键合图结构和混合因果关系的条件下,矩阵变换建模法可以无障碍地顺利实施.
(2)对于线性非定常系统,虽然上述变换操作可以实现,但特定时刻的(即仅是某个时间点处的)实参A、B矩阵将不具有全程效力,必须逐时间点对相关矩阵元素作数值上的修正,这意味着建模过程和仿真过程必须同步进行.虽然逐时间点多次建模在操作上并无障碍和不可,但多次建模无疑将耗费大量的计算时间,尤其对于复杂大系统,因其仿真的计算时间问题比较突出,将会对仿真的计算效率产生显著影响.
(3)对于非线性系统,因场方程、结型结构方程和系统状态方程及其相关表达式都可能是非线性的,则 会有
这将使无论是结型结构方程还是系统状态方程,均呈现很复杂的隐式表达形式,甚至连状态矩阵A和输入矩阵B都根本不存在.故此,对于非线性系统,矩阵变换建模法的实用价值将远远小于其理论价值;因为在建模操作中,相应的矩阵变换等数学手段难以顺畅地实施.
(4)对于存在混合因果关系的键合图模型,储能场将被人为地划分为对应积分因果关系的独立储能场和对应微分因果关系的非独立储能场.在线性系统的情况下,两种储能场的场方程可分别表示如下.
独立储能场:

非独立储能场:
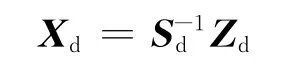
故此,结型结构方程中各关系式将含有非独立储能场输出变量Xd的导数项X·d,使方程的表达结构明显复杂化.虽然从这种结型结构方程出发建立相应的系统状态方程在理论上是可行的,但要通过数学变换消去作为中间变量的Xd、Zd、Din和Dout,使之成为仅含独立储能场能量变量Xi和系统输入量U的最终形式,其过程将十分复杂.之所以如此,是因为独立储能场和非独立储能场常常是耦合关联的,其各自的变量相互间也耦合关联,由此构成具有较大处理难度的代数环问题.所谓代数环,意指某个(些)状态变量导数的定义表达式中出现了该导数本身,形成了递归表达;而且严重时各导数相互定义表达的情况也在所难免,此为多代数环耦合表达,属于代数环问题中更难处理的一类.事实上,由式(5)可见,当因混合因果关系以及非标准型键合图(见下文)所导致的代数环现象存在时,必有矩阵JLL≠0,此时要想顺利实施建模甚至解耦操作,矩阵(I-JLLL)的逆阵必须确保存在,而这一充要条件并非在任何情况下都能满足.
可以证明,如果系统为非线性且具有混合因果关系所导致的代数环问题,在理论上,系统状态方程将为如下的隐性形式:
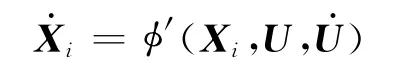
而要经过数学变换手段推导出该方程的具体表达形式,几乎是仅有理论意义而并无实际操作的可能.
(5)对于非标准型键合图模型,因其与具有混合因果关系的键合图模型一样,会导致代数环现象发生,则应用矩阵变换建模法的难度与之相同.
(6)矩阵变换建模法的另一显著特征是必须在实参形式下操作,因此它只有在线性定常的情况下才能“一劳永逸”,否则必须与仿真计算同步实施多次建模操作,这不仅将耗费相当的计算时间,而且也与通用仿真软件开发中的模型“一模多用”原则相悖.
4 矩阵变换建模法应用实例
为进一步说明和验证矩阵变换建模法在特定条件下的可行性和合理性,下面给出先导式溢流阀调压系统[5]的应用实例.
首先作如下假设:
(1)系统是一个完全线性且定常的系统;
(2)系统键合图是标准型键合图,其因果关系设定无需人为指定;
(3)系统中不存在混合因果关系.
图2为系统的键合图模型.
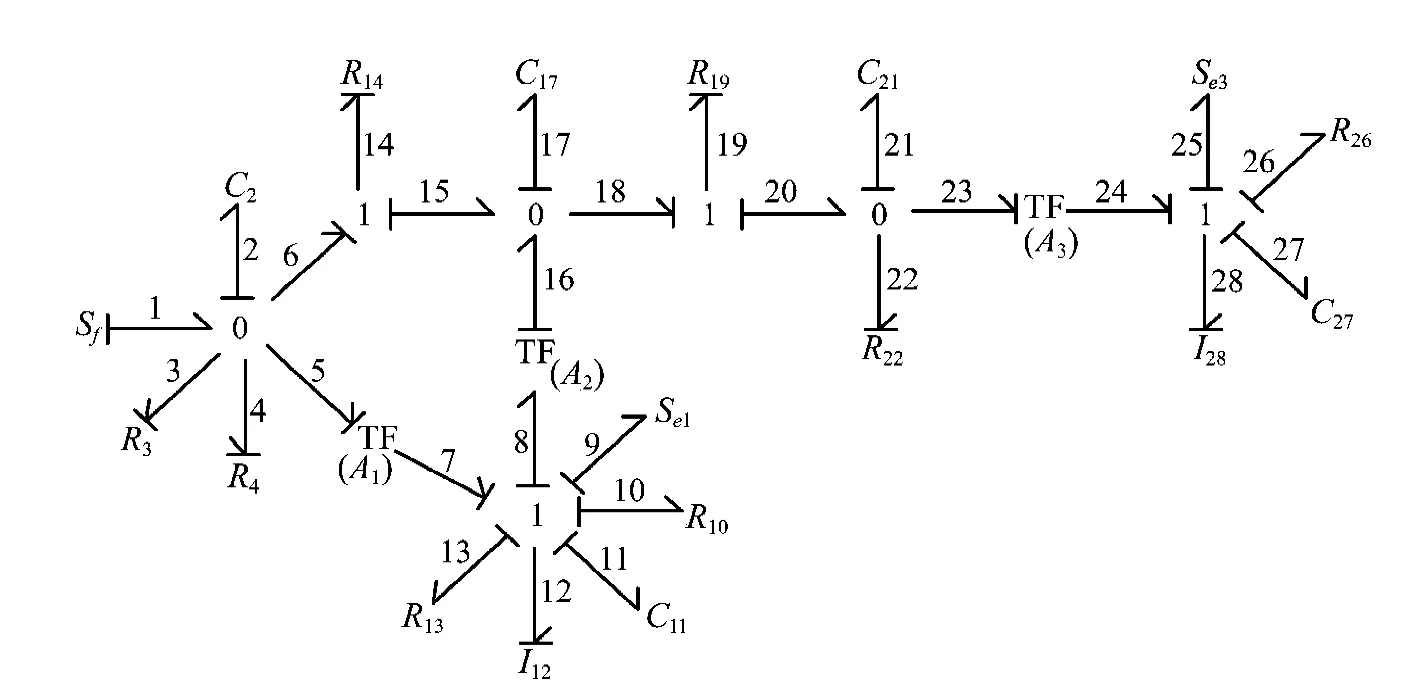
图2 系统键合图模型Fig.2 Bond graph model of system
确定各相关向量和矩阵的方法如下:
(1)能量向量X

(2)共能向量Z
由各储能元的输出变量,可得共能向量为

(3)方阵S
由各储能元键上能量变量和共能变量之间的对应关系,如p2=V2/C1,可得矩阵S,同时可知S为7阶方阵,其非主对角线上元素均为零,如下所示:

(4)耗能场的输入向量Din和输出向量Dout
本例键合图中共含有8个耗能元,其中,有5个的因果线标在不靠近结点端,故其对耗能场的输入为力变量e,输出则为流变量f;另外3个的因果线标在靠近结点端,其输入为流变量f,输出为力变量e,如表2所示.

表2 各耗能元的输入、输出变量Tab.2 Input and output variables for different energy dissipation elements
于是,可得

(5)方阵L
由各耗能元键上输入变量和输出变量之间的对应关系,如q3=p3/R3,F10=R10v10,可知L为8阶方阵,其非主对角线上元素均为零,如下所示:
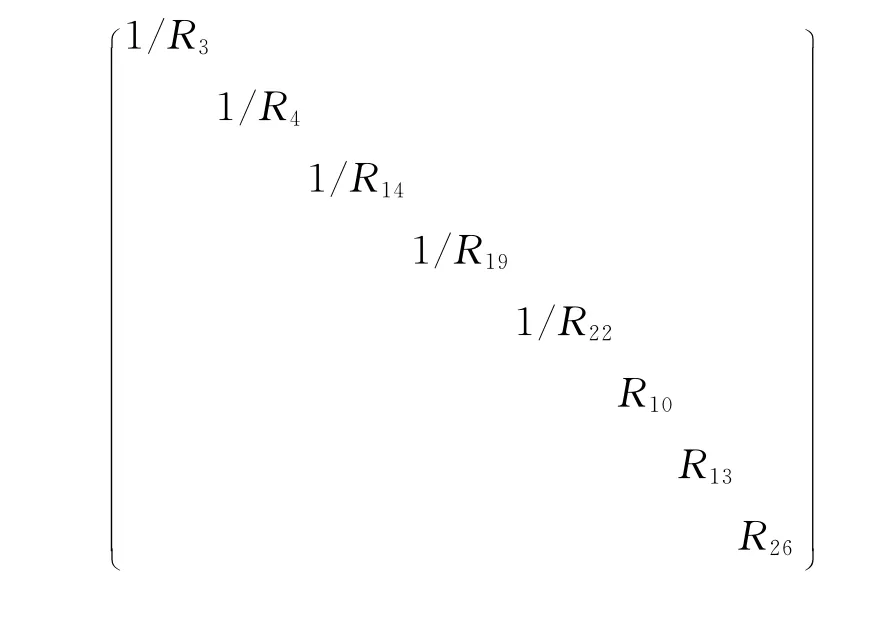
(6)矩阵JSS
参照图2的键合图结构,可得矩阵JSS.因本例有7个储能元,故矩阵JSS是一个7阶方阵,如下所示:

显然,JSS是一个反对称矩阵,这是由能量流动的本质特征所决定的.任一部分功率流,从一个结点流出(输出),必定是要流向另一结点(输入).矩阵JSS的这一性质,为检验模型的正确性提供了方便.
(7)矩阵JSL
由于本例中能量向量X为7阶向量,而耗能场输出向量Dout为8阶向量,故JSL为7×8阶矩阵.
参照图2的键合图结构,可得矩阵JSL如下所示:

可见,矩阵JSL的特征是其所含非零元素均为1或-1,这是由键合图上0结点的流变量代数和为零和1结点上力变量代数和为零的性质及特征所决定的.
(8)矩阵JSU
从图2可见,3个系统输入变量Sf、Se1和Se3均在其所处的结点上直接参与流变量或力变量的平衡,由此可得矩阵JSU,且可知它是一个7×3阶的矩阵.其中的非零元素为

(9)矩阵JLS
矩阵JLS是耗能场输入向量Din与共能向量Z之间的关联矩阵.
依据前述Din和Z的构成,结合0结点上各键力变量相等、1结点上流变量相等及1结点上力变量代数和为零等规则,不难得出如下关系式:

由以上各式可得矩阵JLS.依据Din和Z的阶数,可知JLS是8×7阶矩阵,如下所示:

对比矩阵JLS和JSL,可见二者互为负转置矩阵,这一性质也可用来作模型正确性检验.
(10)矩阵JLL
根据前述假设条件,对于标准型键合图且无混合因果关系的情况,Din元素的表达式在推导中不会出现递归现象,即无代数环现象,故可知JLL=0.
(11)矩阵JLU
矩阵JLU所表征的是结点上无储能元存在,相应的共能变量由对应的源来代为确定的情况;若将图2中的C2去掉,并将输入改为恒压元Se,则各R键上的流量qi将是Se的函数.根据本例假设条件,JLU=0.
至此,各关联矩阵定义完毕,接下来的工作是建立系统状态方程.
由于所需的各向量和矩阵均已确定,则这一过程变得十分简单,只要按照结型结构的理论规则将各向量和矩阵进行组合并实施相应的矩阵变换,即可求出状态矩阵A和输入矩阵B的具体形式,从而完成建模过程.
特别是,在本例中,由于有JLL=0和JLU=0,建模操作大为简化.其中

限于篇幅,本文将不再给出状态矩阵A的具体推导变换过程及最终完整结果,这里仅以矩阵A的左上角元素A11的形成过程为例,略作展示:因为(JSS)11=0,所以(JSSS)11=0.又据上文矩阵JSL,有(JSL)11= (JSL)12= (JSL)13=-1.则得
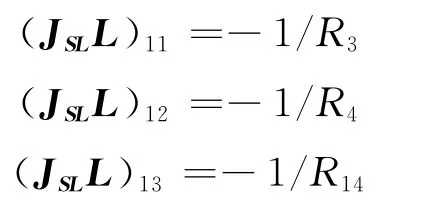
且据上文矩阵JLS,有(JLS)11= (JLS)21= (JLS)31=1,故(JSLLJLS)11=-(1/R3+1/R4+1/R14),及(JSLLJLSS)11=-(1/R3+1/R4+1/R14)/C2.
最后,得

作为对比,在人工推导建模时,有

将两种方法的建模结果相比较,可知二者完全相同.
由此可断定,对于符合特定条件(尤其是线性条件)的系统,矩阵变换建模法是很方便适用的,且所得建模结果同人工推导状态方程的结果完全一致,从而验证了该方法的可行性和合理性.
5 结 论
(1)对结型结构的理论作用和意义应予充分肯定.它从能量场的高度,借助严密的数学手段,明确而严谨地阐述了键合图模型结构的基本特征、能量和物理属性,以及各种动态影响因素的作用特征、特性和规律,同时清晰地给出了从键合图模型向系统数学模型即状态方程转化过渡的数学实施方法即矩阵变换建模法.结型结构理论和矩阵变换建模法的提出与不断完善,为键合图技术的发展奠定了有特色的理论基础,也对该项技术的广泛应用起到了重要的推动作用.
(2)从实用角度看,对于线性、定常且无非标准型键合图结构及混合因果关系(即代数环)的系统,矩阵变换建模法是十分有效的,尤其便于实现自动建模和通用仿真软件的开发.即使对于非定常系统,只要对相关矩阵和向量中的时变元素单独提出并处理,则方法仍可适用.
(3)利用该方法所给出的有关矩阵的数学性质,可以很方便地进行模型正确性的检验和判定,这应视为键合图结型结构理论和矩阵变换建模法的一个鲜明特色.
(4)对于一般的非线性系统,由于在非线性因素建模处理上的难度和障碍,该方法的实用效能将显著降低,特别对于非线性因素较多的复杂大系统而言,单独使用将难以奏效,而必须同其他方法相结合.
(5)对于含有非标准型键合图结构和混合因果关系的系统,若系统是线性的,矩阵变换建模法尚可采用,但实施过程将会很复杂和繁琐;而若是非线性系统,则因建模实施的难度太大,则该建模方法仅具有理论意义,除非对极个别的特殊简单情况,一般难以实际采用.
[1]Rosenberg R C.State-space formulation for bond graph models of multiport systems[J].Journal of Dynamic Systems,Measurement,and Control,1971,93(1):35-40.
[2]Ort J R,Martens H R.The properties of bond graph junction structure matrices [J].Journal of Dynamic Systems,Measurement,and Control,1973,104(4):362-367.
[3]Karnopp D C,Rosenberg R C.System Dynamics:A United Approach [M].New York:John Wiley &Sons,Inc.,1975.
[4]Karnopp D C,Margolis D L,Rosenberg R C.System Dynamics: Modeling and Simulation of Mechatronic Systems[M].4thed.New York:John Wiley &Sons,Inc.,2005.
[5]Dransfield P.Hydraulic Control Systems— Design and Analysis of Their Dynamics [M].Berlin:Springer-Verlag,1981.
