土壤模型对地表电位影响及合理选取土壤模型方法研究*

李文峰 杨洪耕 肖先勇 李兴源

(四川大学电气信息学院,成都 610065)

(2013年1月4日收到;2013年1月22日收到修改稿)

1 引言

当前,能源和环境问题成为全世界普遍关注的问题,高压直流输电具有稳定和调度控制性能优越、可有效限制短路容量、长距离大容量输电经济性显著及节约走廊等优点,在中国实现西电东送、南北互供的电网发展战略中扮演着重要角色,对解决能源分布与负荷中心不平衡都具有重要意义[1-3].在直流输电工程中,单极大地回路运行时直流接地极的入地电流达数千安,强大的直流电流长时间持续流过接地极,会产生一系列负面效应：对地下金属管道和电力系统接地网产生电化腐蚀[4,5],引起变压器直流偏磁[2,6-8]等,后者造成变压器振动剧烈、噪声聚升、过热等一系列问题,严重时甚至可引起变压器损坏,影响到电网安全稳定运行.

分析入地直流对交流系统影响,需要首先求出地表电位(ESP)[9-11],这需要求解满足一定边界条件的拉普拉斯方程得到其格林函数[12,13].目前大尺度范围内ESP仿真结果不够准确[14-17],导致对流过直流接地极附近的一些变电站中性点直流量评估失真,其中最主要的原因是实际土壤结构在大尺度范围内复杂多变,难以构造合适的土壤模型来定量计算ESP分布[14-16].目前普遍采用的是水平和复合分层土壤模型,文献[9—11]基于水平分层土壤模型计算了地表电位;文献[15]分析了海洋对流入变压器中性点直流电流量的影响,对靠近海边的变压器更容易发生直流偏磁现象给予了解释;文献[16,17]分析了土壤结构对流入变压器中性点直流电流的影响,指出在建立土壤模型时应重点研究表层土壤结构的影响.

然而,如何构造适当土壤模型来定量计算大尺度范围内ESP一直是尚未有效解决的难题[14-17].对于距离接地极数百公里区域来说,土壤电性结构变化很大,建立一个完全符合实际的土壤模型几乎不可能[15],而且随着土壤分层复杂化,接地计算也越来越困难.因此,如何选取合理的土壤模型,既不至于工作量过大,又能得到准确可靠的计算结果就显得尤为重要.为此,本文在前人工作的基础上,首先利用物理意义明确的模拟镜像法推导出三维复合分层土壤模型格林函数,基于特定土壤模型,计算了土壤模型变化给ESP带来的变化,结果表明满足一定条件时,即可确定土壤模型,以避免构建更复杂的模型以记及更大地理范围、更精细的土壤结构,并通过理论推导和数值仿真给出了判据及其阈值.研究成果对于充分发挥直流输电的独特优势、减小其不利影响具有一定指导意义.

2 理论计算方法及验证

2.1 理论计算方法

图1为三维复合分层土壤模型示意图,S(x0,y0,z0)为点电源,平面xOy代表地平面.z轴方向水平分3层,各层土壤电阻率和层厚分别为ρz1,ρz2,ρz3和 z1,z2-z1,∞;然后把 z轴方向水平第1层土壤在x轴方向竖直分3层,各层土壤电阻率和层厚分别为 ρx1,ρx2,ρx3和 ∞,x2-x1,∞;最后把x轴方向竖直第1层土壤在y轴方向竖直分3层,各层土壤电阻率和层厚分别为ρy1,ρy2,ρy3和∞,y2-y1,∞.

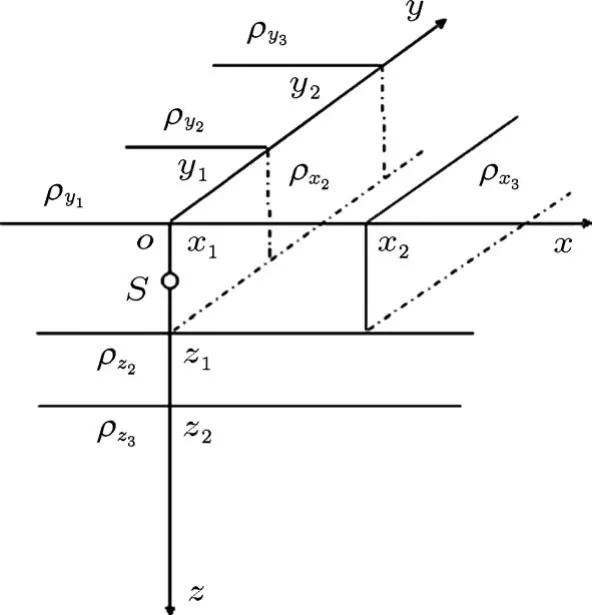
图1 三维复合分层土壤模型

若x,y轴方向土壤不分层,把图1水平第1层看作是电阻率为ρx1的均匀土壤,即ρz1=ρx1,则三维复合分层土壤模型转化为水平分层土壤模型,除点电源S处,点源在其他各空间位置产生的电位U均满足拉普拉斯方程[18,19]：

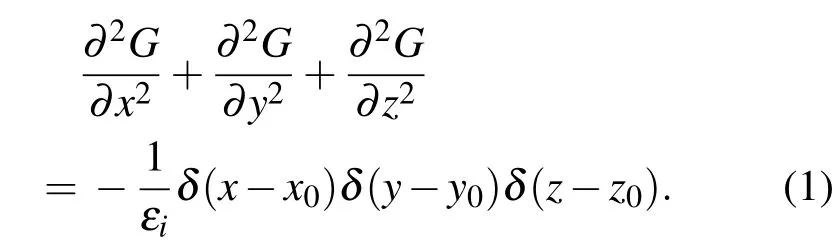
通过傅里叶变换,得到频域拉普拉斯方程[20,21]：

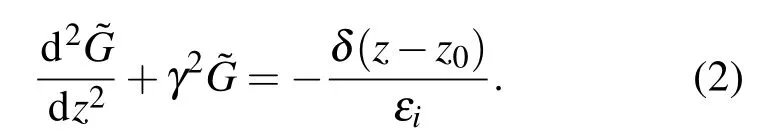
若点源和场点均置于第1层土壤,可得频域格林函数为

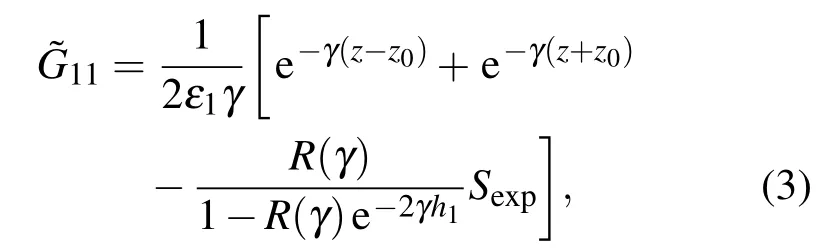
其中,

选取准动态镜像点bzi,用点匹配法拟合[22,23],可得

其中bzi为实数,azi为复数,在模拟镜像法中,避免了复镜像法中复杂的Prony法[24]或GPOF法计算,与复镜像法相比数值稳定性更高.另外,模拟镜像法在选取镜像的位置上有较大的随意性,而复镜像法的采样点必须选在kz平面上的某些固定路径上.本文是根据经典镜像理论来选取镜像的位置,物理意义非常明确.

把(4)式代入(3)式,进行傅里叶逆变换得直角坐标系中格林函数：

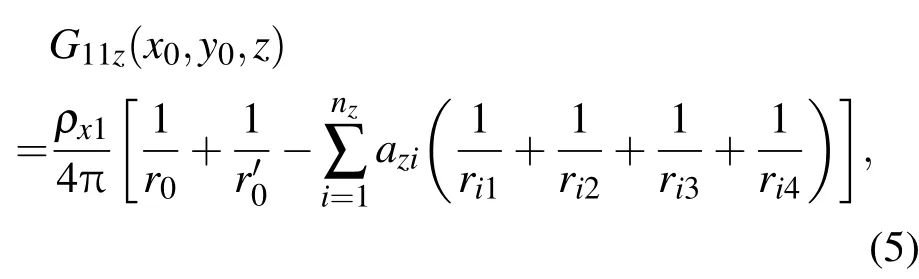
式中,

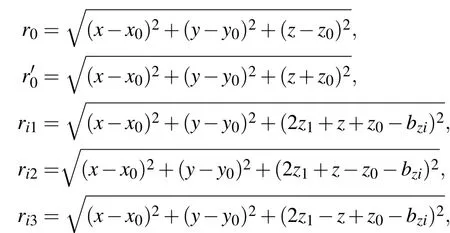
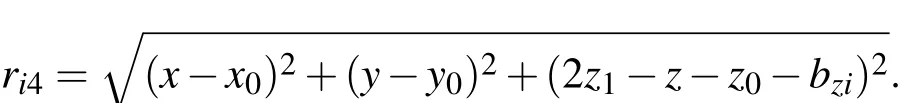
图1中x方向为竖直3层土壤模型,其格林函数的求解和水平分层相同,当点源和场点均在第1层时,可得到直角坐标系下的格林函数：

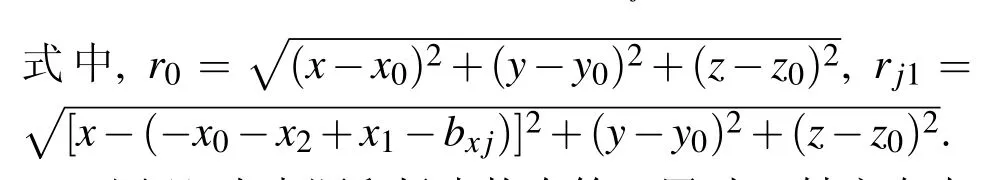
同理,当点源和场点均在第1层时,y轴方向直角坐标系下格林函数表达式为[

]

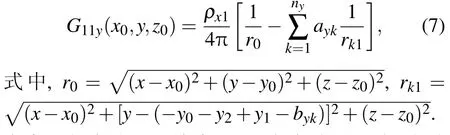
在实际竖直分层土壤中,还要考虑地面影响,这时格林函数表达式是(6),(7)式加上源点的镜像作用,即分别把(6),(7)式中z0替换为-z0.

从(6)式可知,在x方向竖直分层土壤模型中,镜像点y和z坐标不变,仅x坐标变化,可以想象在x轴方向匹配有几个镜像点,在它们作用下x方向竖直分层边界条件得以满足.因此,在这几个镜像点作用下,可以将上层土壤看作是电阻率为ρx1的均匀土壤.这时三维复合分层土壤模型变成二维复合分层土壤模型,而上述的镜像点就可以看作是在x轴方向竖直第1层中的源点.为了满足y轴方向的边界条件,这些镜像点须根据(7)式的关系,再在y轴方向镜像,这时二维复合分层土壤模型转化为水平分层土壤模型,而上述的镜像点就可以看作是z轴方向水平第1层中的源点.同理,为了满足z轴方向的边界条件,这些镜像点根据(5)式的关系,再在z轴方向镜像.在上述所有镜像点作用下,求出的电位表达式就是三维复合分层土壤模型的格林函数[17].

由上可知,当点源和场点均在x,y,z方向第1层时,三维复合分层土壤模型下格林函数可以写为

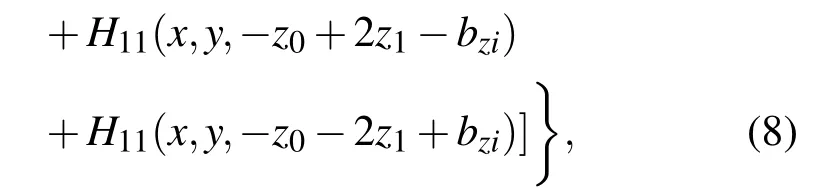
式中,

若源点和场点在不同土壤层,则相应地改变水平分层模型和垂直分层模型镜像点位置及大小,按照上述方法即可求得相应的格林函数.

2.2 理论有效性及可信性

本文根据推导的三维复合分层土壤模型格林函数开发了ESP计算程序.为了验证本文方法的有效性及可行性,在相同参数条件下与文献[11]计算结果进行了比较.文献[11]分别采用简易算式和CDEGS仿真软件计算了晋东南地区(晋城、长治)各主要站点ESP,分析了山西-江苏±500 kV高压直流输电工程直流单极运行后对晋东南地区220 kV及以上变电站的影响.其中,土壤参数为：电阻率 ρz1,ρz2,ρz3分别为 0.2,10,0 kΩ·m,层厚hz1,hz2分别为4,30 km,接地极采用双环设计,入地电流3000 A,埋深3 m.得到镜像位置分别为 bz1=26,bz2=34,bz3=60,bz4=42 km,相应幅值分别为az1=-28.91,az2=56.84,az3=22.31,az4=-51.88.CDEGS仿真软件是计算ESP比较权威的方法,三维复合分层土壤模型是作者在总结前人工作基础上所提出,故将本文三维模型过渡到水平分层土壤模型,在相同的计算参数下用模拟镜像法计算了ESP,与文献[11]计算结果进行了比对研究,结果表示在图2中.从图2可以看出,随着距离接地极距离(r)的增加,ESP逐渐减小,约呈负指数衰减趋势,本文计算结果与文献[11]中CDEGS软件仿真结果符合得很好,与简易算式计算结果相比精度有较大提高,验证了本文方法的可靠性,表明本文方法和模型可以用于计算流过变电站中性点直流量.实际土壤结构复杂且变电站分布比较广泛,合理选择土壤模型对有效分析流过变电站中性点直流量问题具有重要意义,本文模型可以考虑实际土壤同时在三维方向的变化,能够更加准确地模拟实际土壤,采用三维复合分层土壤模型有助于准确计算ESP.

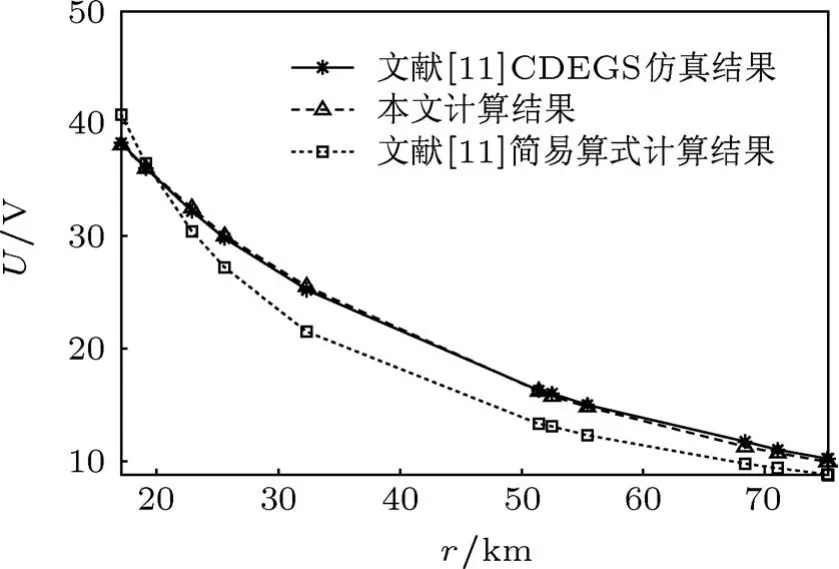
图2 本文计算结果与文献[11]对比研究

3 土壤模型选取方法

3.1 水平分层土壤模型选取方法

为研究水平分层土壤模型选取方法,假定土壤模型A为水平3层,土壤模型B为水平2层,B和A前两层土壤参数相同.A模型参数为：电阻率ρz1,ρz2,ρz3分别为 1,2,10 kΩ·m,层厚 hz1,hz2分别为 5,30 km.土壤模型变化对ESP的影响记为ΔESP,分析了第1,2层土壤参数对ΔESP的影响,结果列于表1中.直流接地极由直径为600 m的单圆环构成,埋深4 m,入地电流为3000 A.

从表1可以看出,第1,2层土壤参数均对ΔESP带来影响,随着极距的增加ΔESP越来越小,ΔESP约与Δr成正比例关系,由于模型A和B前两层土壤参数完全相同,故ΔESP即表示第3对ESP带来的影响,ΔESP越小,表明第3层对ESP的影响越小.随着ρz1的变小或hz1的变大,ΔESP越来越小且随着极距的变化越来越均匀,表明随着ρz1的变小或hz1的变大,第3层对ESP的影响越小且越均匀.

从表1还可以看出,对于相同极距,当hz2不变时,若ρz2＞ρz1,随着ρz2的变大,ΔESP越来越小,若ρz2＜ρz1,随着ρz2的变小,ΔESP越来越小;当ρz2不变时,无论ρz2＞ρz1或ρz2＜ρz1,随着 hz2的变大,ΔESP越来越小.另外,随着|ρz2-ρz1|或hz2的变大,ΔESP随极距的变化越均匀,即某土壤分层与表层电阻率相差越大、层厚越大,其下各土壤分层对表层ESP的影响越均匀.在评估流过变电站中性点直流电流时,关心的是变电站间电位差且变电站大多建在距离接地极数十千米之外,故当某土壤分层与表层电阻率相差较大、层厚较大时,忽略其下各层对变电站间电位差的影响在工程上是允许的,这将减小土壤模型的复杂度,易于编程且具有较高的准确性.

表1 第1,2层土壤参数对ΔESP的影响(ρz1,ρz2/kΩ·m,hz1,hz2/km)

由上分析,B型相当于A模型的简化,简化效果与第1,2层土壤参数密切相关,若简化效果用k评价,当ρz2＞ρz1时,简化效果约与ρz2,hz1和hz2成正比,约与ρz1成反比,即k∝ρz2hz1hz2/ρz1;当ρz2＜ρz1时,简化效果约与ρz1,hz1和hz2成正比,约与ρz2成反比,即k∝ρz1hz1hz2/ρz2.这可做如下解释：

(a)水平三层模型中,设ρz2≫ρz1,hz2≫hz1,则每单位长度上由上层土壤流入中间层的电流很小,在计算中可以假定上层土壤中入地电流的方向近似水平;又因为ρz3极小,在计算中可以近似认为入地电流垂直穿过中间层进入第3层流动,在上层土壤中[11]

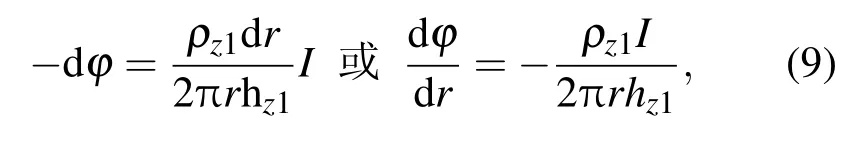
中间层土壤中

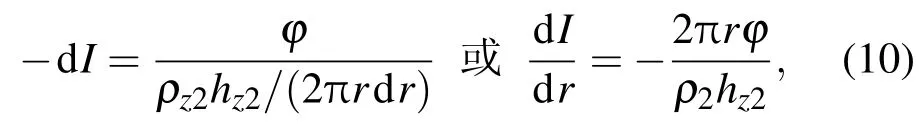
式中,直流地表电位为φ,上层土壤中的电流为I,入地总电流为I0,r为某站点到电流注入点的距离.

由(9)和(10)式,并设x1=,x2=

,X=jx1x2r,得零阶贝塞尔方程

其解为φ(r)=C1J0(jx1x2r)+C2H0(jx1x2r),J0,H0分别为第一、三类零阶贝塞尔函数.将φ(r)对r求导,并代入(9)式得：

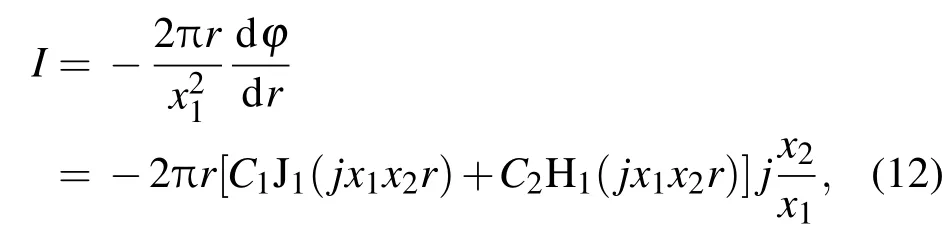
式中,J1,H1分别为第一、三类一阶贝塞尔函数.J0具有在r=0时为有限值的性质,H1具有当r→∞时为0的性质.根据边界条件求得：

由文献[25]可知,随着x1x2r的增大(也即r的增大),电流将很快在上层土壤中消失,当x1x2r=4时,流经上层的电流只有全部入地电流的5%,此时即可认为电流已基本上全转入第3层流动.故可得电流基本转入下层流动的距离为

上式表明土壤参数ρz1,ρz2,hz1和hz2将直接影响到电流转入下层的速度,上层土壤越厚,ρz2/ρz1越大,电流在上层土壤中消失得越慢,电流进入第3层的速度越慢,那么ESP受第3层的影响越小,土壤模型简化对ESP带来的影响也越小.

(b)同理,设ρz2≪ρz1,hz2≫hz1,ρz2极小且ρz3极大,可得电流基本转入第3层流动的距离为

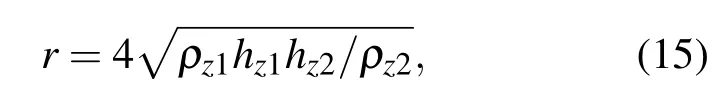
上式表明土壤参数ρz1,ρz2,hz1和hz2将直接影响到电流转入下层的速度,中层土壤越厚,ρz1/ρz2越大,电流在中层土壤中消失得越慢,电流进入下层越慢,那么ESP受第3层的影响越小,土壤模型简化带来的影响也越小.

由上述分析可见,土壤模型简化效果主要与表层和待估层的电阻率和层厚有关,设待估层电阻率和层厚为ρi,hi,表层电阻率和层厚为ρ1,h1,那么ρi＞ρ1时,α1=越大,简化土壤模型效果越好;ρi＜ρ1时,α2= 越大,简化土壤模型效果越好.待评层与表层距离越大,简化土壤模型效果越好.因此,虽然本文分析中所用的模型是特定的,但由此得到的结果却具有普遍性.通过大量仿真表明,当ρi＞ρ1时,若α1＞2.6×104,忽略ρi以下各层基本上不改变变电站间电位差,可作为判断能否简化土壤模型的阈值;当ρi＜ρ1时,阈值α2＞2.6×104.

3.2 竖直分层土壤模型简化方法

用同样的方法研究了竖直分层土壤模型简化方法,结果列于表2中.其中,原始土壤模型参数：电阻率 ρx1,ρx2,ρx3分别为 1,1.5,5 kΩ·m,第 2 层分界面hx1,hx2分别距接地极30,50 km.直流接地极处于竖直第1层,由直径为600 m的单圆环构成,埋深4 m,入地电流为3000 A.

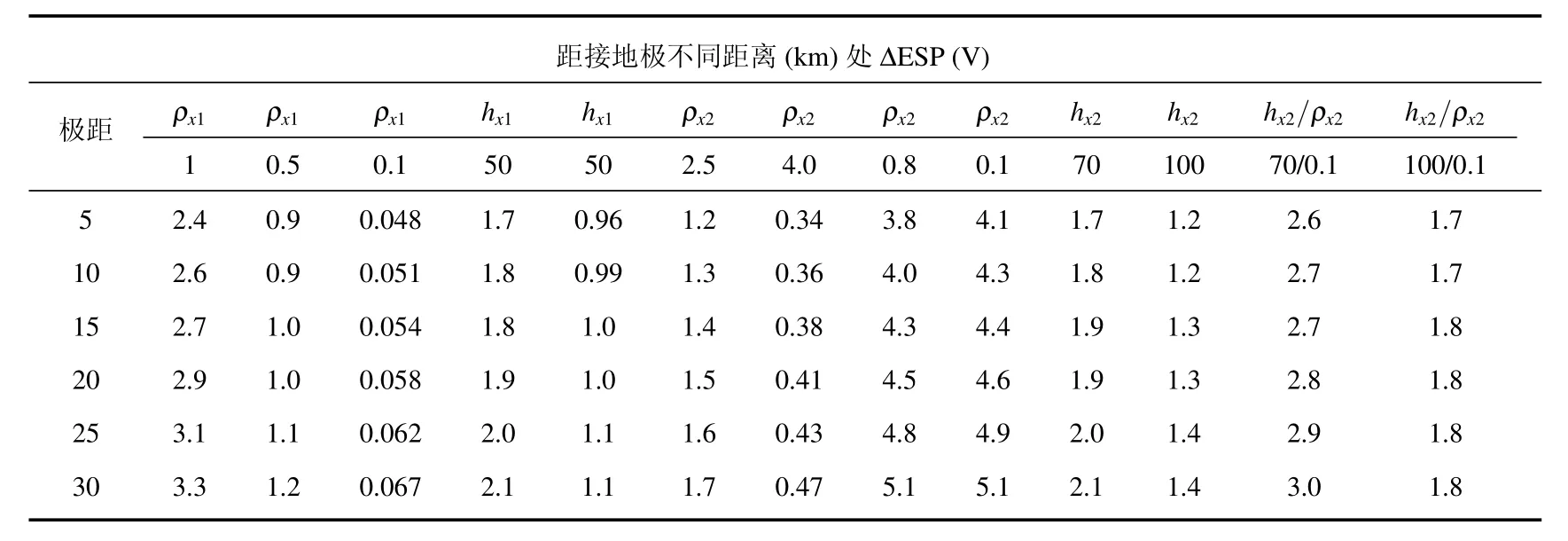
表2 第1,2层土壤参数对ΔESP的影响(ρx1,ρx2/kΩ·m,hx1,hx2/km)

从表2可以看出,竖直分层土壤模型下模型简化对ΔESP的影响规律与水平分层模型相似,随着|ρx2-ρx1|或hx2-hx1的变大,第3层对第1层ESP的影响变小且影响变均匀,即某土壤分层与目标层电阻率相差越大、层厚越大,其后各土壤分层对目标层ESP影响越小.同样,当ρx2＞ρx1时,可用β1=来衡量简化效果,β1越大,电流进入第3层速度越慢,那么ESP受第3层影响越小,土壤模型简化效果也越好;当ρx2＜ρx1时,β2=越大,简化效果越好.通过大量仿真表明,竖直分层土壤模型下阈值β1,β2约为3.9×104,当大于阈值时,在评估流过目标层变电站中性点的直流量时,忽略其后各层在工程上是允许的.

3.3 三维复合分层土壤模型简化方法

三维复合分层土壤模型下土壤分层更加复杂,将上述水平和竖直分层土壤模型简化判据应用到复合分层土壤模型,当满足判据要求时即可确定土壤模型并准确求得流过变电站中性点的直流量,从而避免考虑更加复杂的分层情况.

4 三维复合复层土壤模型下模型简化对流过变压器中性点直流量的影响

为验证土壤模型简化方法的有效性,进行如下算例分析,原始土壤模型为三维复合分层土壤模型,如图1所示.土壤模型参数：ρy1,ρy2,ρy3,ρx2,ρx3,ρz2和ρz3分别为 0.5,10,5,0.1,1,20和2 kΩ·m;y1,y2,x1,x2,z1和z2分别为50,100,0,40,40和360 km;得α1,β2x,β2y分别约为 7.6×105,6.1×104和2.2×105,均大于阈值.因此可以把土壤模型简化为x,y方向竖直2层和z方向水平2层.为验证推断的可靠性,基于场路耦合算法,计算了土壤模型简化前后流过变电站B,C中性点的直流电流,并比较了不同交流网络参数下效果,结果列在表3中.直流接地极与交流网络相对位置和连接关系如图3所示.其他计算参数如下：

1)直流接地极坐标为(-150,0,0.004),交流电网全部处于x,y竖直第1层,变电站B,C坐标为(-120,0,0.0008),(-20,0,0.0008),杆塔间距为0.5 km,输电线路长度为100 km;

2)直流接地极由800和600 m的同心圆环构成,埋深4 m,接地极入地电流5 kA;

3)变电站接地网为150 m×150 m,埋深0.8 m;杆塔接地体为15 m×15 m,埋深1 m;

4)假设输电线路为单回220 kV线路,每相导线单位长度直流电阻为0.09Ω·km,地线单位长度直流电阻为2.5Ω·km,忽略变压器绕组电阻.

图3 直流接地极与交流网络相对位置和连接关系

表3 选取不同土壤模型对流过变压器中性点直流电流(I/A)的影响

从表3可以看出,原土壤模型简化后,流过变压器中性点的直流电流量基本不变,且随着交流线路回数和变电站接地电阻变化,简化效果仍然较好,证明了本文所提土壤模型选取方法的有效性.

5 结论

针对如何构造合理土壤模型来准确计算流过变压器中性点的直流电流难题,首次利用物理意义明确的模拟镜像法推导出三维复合分层土壤模型格林函数,基于水平和竖直分层土壤模型,分析了不同土壤配置下土壤模型对ESP的影响,提出了合理选取土壤模型的判据及其阈值.结论如下：

1)水平(竖直)分层土壤模型下,随着极距r的增加,待估层对ESP影响减小,ΔESP约与Δr成正比例关系;待估层与表层(目标层)电阻率相差越大、层厚越大,ΔESP随r变化越均匀,即ΔESP随Δr变化越缓慢;从理论上论证了待估层对ESP的影响规律,表明ΔESP与电流流入待估层速度有关,电流进入待估层速度越慢,待估层对ESP影响越小且越均匀,反之待估层对ESP影响越大;

2)水平(竖直)分层土壤模型下,待估层与表层(目标层)电阻率相差越大、层厚越大,待估层对ESP影响越均匀,当满足下面(3),(4)判据时,忽略待估层以下(后)各层仅改变ESP绝对值,基本不改变各点电位差,从而可以确定土壤模型,避免土壤模型选取的盲目性和随意性;

(4)竖直分层土壤模√型下,可用 β1=(ρi＞ ρ1)或 β2=(ρi＜ ρ1)评估待估层对ESP的影响程度,β1,β2越大,待估层对ESP的影响越均匀,β1,β2≥3.9×104时,选取土壤模型时可以忽略ρi以后各层;

5)三维复合分层土壤模型下土壤分层更复杂,运用结论3)和4)可有效减少模型复杂度,易于编程且具有较高精度.

[1]Jiang X L,Wang S H,Zhang Z J,Hu J L,Hu Q 2010 IEEE Trans.Dielectr.Electr.Insul.17 71

[2]Li X P,Wen X S,Markham PN,Liu Y L 2010 IEEE Trans.Power Del.25 2504

[3]Liao K,He ZY,Li X P2012 Automation of Electric Power Systems36 1(in Chinese)[廖凯,何正友,李小鹏2012电力系统自动化36 1]

[4]Wei D J 2008 Power System Technology 32 75(in Chinese)[魏德军2008电网技术32 75]

[5]Dong X H,Yang W,Tang C,Liu G 2009 High Voltage Engineering 35 1546(in Chinese)[董晓辉,杨威,唐程,刘刚2009高电压技术35 1546]

[6]Boldue L,Granger M,Saintonge J 2005 IEEE Trans.Power Del.20 163

[7]Zeng R,Yu ZQ,He JL,Zhang B,Niu B 2011 IEEETrans.Power Del.26 2785

[8]Zhu Y Y,Jiang WP,Zeng ZH,Yin Y H 2005 Proceedingsof the CSEE 25 1(in Chinese)[朱艺颖,蒋卫平,曾昭华,印永华2005中国电机工程学报25 1]

[9]Hao Z G,Yu Y,Zhang B H,Cheng L Y,Cao R F,Ding M S,Zhang J 2009 Electric Power Automation Equipment 29 10(in Chinese)[郝治国,余洋,张保会,程临燕,曹瑞峰,丁茂生,张军2009电力自动化设备29 10]

[10]Villas JET,Portela CM 2003 IEEETrans.Power Del.18 867

[11]Ren Z C,Xu JG,Zhang Y K,Zhen W,Wu GN 2011 Transactionsof China Electrotechnical Society 26 256(in Chinese)[任志超,续建国,张一坤,甄威,吴广宁2011电工技术学报26 256]

[12]Xiao CY,Lei Y Z 2005 Acta Phys.Sin.54 1950(in Chinese)[肖春燕,雷银照2005物理学报54 1950]

[13]Liang CH,Zhu QX 2002 Acta Phys.Sin.51 2202(in Chinese)[梁昌洪,褚庆昕2002物理学报51 2202]

[14]Zhang B,Zeng R,He J,Zhao J,Li X,Wang Q,Cui X 2008IETGener.Transm.Distrib.2 185

[15]Liu Q,Zheng JC,Li L C 2007 Ph.D.Dissertation(Beijing：Tsinghua University)(in Chinese)[刘曲,郑健超,李立涅2007博士学位论文(北京：清华大学)]

[16]He JJ,Ye HS,Lin FC,Li H,Lu Y X,Gui Z 2007 Proceedingsof the CSEE 27 14(in Chinese)[何俊佳,叶会生,林福昌,李化,卢毓欣,桂重2007中国电机工程学报27 14]

[17]Li W F,Yang H G,Xu FW 2012 Journal of Sichuan University:Engineering Science Edition 44 161(in Chinese)[李文峰,杨洪耕,徐方维2012四川大学学报：工程科学版44 161]

[18]Shang Y,Huo BZ,Meng CN,Yuan JH 2010 Acta Phys.Sin.59 8178(in Chinese)[尚英,霍丙忠,孟春宁,袁景和2010物理学报59 8178]

[19]Li Y L,Wang M J2009 Chin.Phys.B 18 2420

[20]Chow Y L,Yang JJ,Srivastava K D 1992 J.Appl.Phys.71 569

[21]Han ZY,Wang HN,Yao JJ,Han ZY,Yang SW 2009 Acta Phys.Sin.58 1608(in Chinese)[韩子夜,汪宏年,姚敬金,韩子夜,杨守文2009物理学报58 1608]

[22]Torabian A,Chow Y L 1999 IEEETrans.Micpowave Theory Tech.47 1777

[23]Shubair R M 2001 IEEE International Symposium on Antennas and Propagation Society Boston,January 7—13,2001 p838

[24]Hou WB,Liu T Q,Li X Y 2010 Acta Phys.Sin.59 3531(in Chinese)[侯王宾,刘天琪,李兴源2010物理学报59 3531]

[25]Xie G R 1991 Power System Grounding Technology(Beijing：China Electric Power Press)p96(in Chinese)[解广润1991电力系统接地技术(北京：中国电力出版社)第96页]