Li-N-H储氢体系热力学性质的第一性原理研究

2013-09-27赵玉娜高涛吕金钟马俊刚

物理学报 2013年14期

关键词：储氢化合物理论

赵玉娜高涛吕金钟马俊刚

1)(北京交通大学海滨学院,黄骅 061100)

2)(四川大学原子与分子物理研究所,成都 610064)

(2013年1月22日收到;2013年4月3日收到修改稿)

1 引言

车载储氢是推进氢燃料车规模化商业应用的重要环节,开发高性能车载储氢材料技术成为当前能源及材料领域关注的热点.近几年来,Li-N-H储氢材料以较高的质量储氢密度赢得了众多研究者的青睐[1-3].据研究表明[3],Li3N的储氢反应过程按如下两步进行：

上述两步反应的吸氢总质量分数为10.4 wt.%.然而在实际的应用中存在许多有待解决的问题,比如吸放氢动力学性能差、吸放氢温度高等.因此了解这些材料的微观结构性质对于理解其储氢机理,研究储氢反应动力学具有重要意义,也有益于改善现有储氢材料的储氢性能以及发展新的轻质储氢材料.据调查对Li-N-H体系相关的一系列化合物进行电子结构、晶体结构动力学性质的研究已有很多[4-6],但是对他们的热力学性质研究仅仅停留在一些实验上,并且研究较少.为了正确理解储氢的微观结构变化,深入认识Li-N-H体系新的物理特性,因此研究Li3N的储氢过程中材料的热力学特性显得尤为重要.密度泛函理论(DFT)已被广泛应用于材料模拟研究中[7-10],本文采用基于密度泛函理论的平面波赝势方法,从Li3N,LiH,Li2NH和LiNH2的电子结构入手,通过晶格动力学特性研究各个化合物和化学反应的热力学性质,其中包括Li3N的储氢过程中各个产物的晶格参数、生成焓和化学反应焓,并与已有的实验及理论数据进行了系统的比较.

2 计算理论

所有计算均采用ABINIT程序包[11],优化过程采用局域密度近似(LDA)作为交换相关函数,赝势选用Troullier-Martins模守恒赝势[12].平面波截断能取30Hartree,总能计算采用Monkhorst-Pack方案对布里渊区进行积分,选择K网格点为4×4×4.采用Gauss smearing方法,参数选择为0.002 Hartree,其他参数均采用默认值.Li3N,LiH,Li2NH,LiNH2和H2的总能计算时采用相同的设置.H2的总能计算采用a=10A˚的简单立方模型,同时对氢分子的内坐标进行了优化.对Li3N,LiH,Li2NH,LiNH2晶体零点能的计算使用线性响应理论和LDA近似,采用模守恒赝势.

3 结果与讨论

3.1 物质的生成焓ΔH

物质的生成焓ΔH能够确定化学反应过程中各种化合物的相稳定性,是研究储氢材料的重要热力学物理量.因化合物的焓H=U+PV(U为体系的内能,P为压强,V为体积)在温度为0 K时的表达式[13]为

其中,Eele为体系的电子总能,EZPE为零点振动的零点能(对于固体分子来说∫ω,m它ax等于整个布里渊区频率求和,即EZPE=3nN0(h¯ω/2)g(ω)dω;对于气体分子如H2和N2分子,零点能EZPE=(1/2)h¯ω0(ω0为温度T=0 K时的振子频率)).

考虑到有限温度对焓的影响后,当温度为T时焓的表达式[14]为

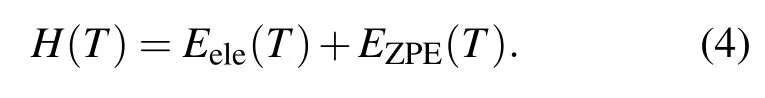
因为温度对电子总能的影响很小,可以采用0 K的电子总能;考虑到气体(视为理想气体)分子平动能、转动能和PV的影响,对线性分子将Etranst(T)+Erot(T)+PV=7/2kBT加到(4)式中(其中Etranst为平动能,Erot为转动能,kB为玻尔兹曼常数),对非线性分子将Etranst(T)+Erot(T)+PV=4kBT项加到(4)式中.振动能Evib采用下列表达式[15]为

为了研究Li-N-H储氢过程中相关化合物的生成焓,本文首先要对涉及的所有物质进行结构优化,计算结果见表1.从表中可见优化的结果和有关的实验及理论数据很接近,误差在5%以内.利用优化的结构得到每种物质的总能量、零点能和振动能,根据上述的理论方法,计算得到储氢反应中每一种化合物的生成焓(在标准状态下相对于元素的生成能),结果由表2中给出.从表中数据可见,计算得到的所有化合物和气体分子在温度为T=0 K的零点能EZPE和生成焓结果和他人实验或理论结果都比较接近,如LiH在0 K时生成焓为-82.6 kJ/mol,和Miwa等[23]的理论结果-81 kJ/mol非常接近,LiNH2和Li2NH的生成焓分别为-191.0和-256.3 kJ/mol,这些结果很接近实验值(-186±9)[24]和(-219±24)kJ/mol[25],只有Li3N在温度为0 K时的生成焓为-175.1 kJ/mol,与实验值-148.7 kJ/mol[25]有点差别,但仍在模拟计算的误差范围之内.同时表2也给出了温度为298 K的振动能和300 K时的振动熵,这些虽然没有理论和实验数据进行比较,但是我们用这些数据计算得到的温度为298 K时化合物的生成焓,本文计算结果和他人的结果符合得非常好,除此之外,和实验的数据相比误差也在10%以内.因此密度泛函理论得到的化合物的生成焓是合理的.为了更直观地看到本文计算的合理性,我们给出了化合物Li3N的热力学函数,包括焓、熵、反应吉布斯自由能和焓对储氢反应的贡献,结果如图1所示.图1中的标注代表了文献中的实验数据[26],可以看到二者明显符合.

3.2 化学反应焓ΔHR

反应焓为化学反应在不同温度下生成物与反应物的焓值之差,表达式为式中HPT为生成物在温度T的焓值,HRT为反应物在温度T时的焓值,求和下标P,R分别指反应中各个生成物、反应物求和.我们研究计算Li3N整个储氢反应在T=0 K时的反应焓为

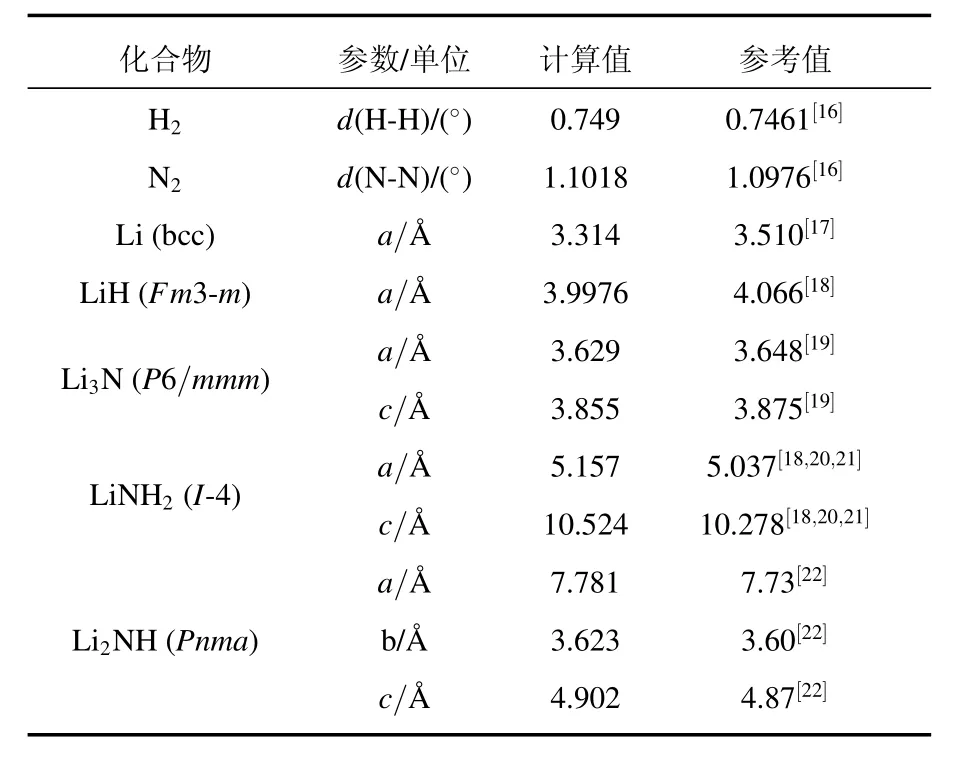
表1 结构参数和参考数据比较(本文计算的固体的空间群信息在表中给出)

图1 Li3N的热力学函数随温度的变化 (a)化合物Li3N在不同温度下的熵;(b)化合物Li3N在不同温度下的焓;(c)化合物Li3N在不同温度下的反应吉布斯自由能;(d)焓(TΔS)对反应3Li+(1/2)N2→Li3N在不同温度下能量的贡献

常温下T=298 K的反应焓为

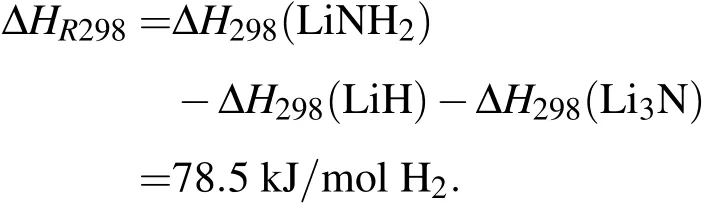
据先前Miwa等[23]给出的此反应的反应焓为ΔH0=-99 kJ/mol H2(仅考虑总能)和-85 kJ/mol H2(包括零点能在内),把零点能考虑进去之后的结果就和Chen等[30]报道的实验值-81 kJ/mol H2符合得非常好.从实际储氢材料的应用来讲,反应焓大约-80 kJ/mol H2意味着生成的氢化物较为稳定,为了降低放氢温度,最好使反应焓接近负值.同时可以看到,T=298 K时上述反应的反应焓为78.5 kJ/mol H2,这和他人计算得到T=300 K的结果75.67 kJ/mol H2[13]非常接近.

如果我们把整个反应分为两步来研究,反应(1)式在T=0 K时的反应焓为

常温下T=298 K时反应焓为

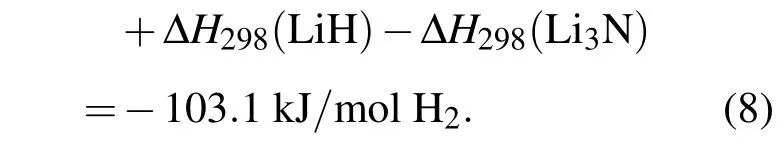
我们看到温度为T=0 K时,计算得到包含零点能的反应(1)的反应焓ΔHR0为-163.7 kJ/mol H2,其结果和Chen等[30]报道的反应(1)式的反应焓为-165 kJ/mol H2非常接近,并且和Akbarzadeh等[32]利用密度泛函理论得到的反应焓-130 kJ/mol H2(不包含零点能)和包含零点能的反应焓-114 kJ/mol H2相一致.

反应(2)式在T=0 K时反应焓为

常温下T=298 K时反应焓为

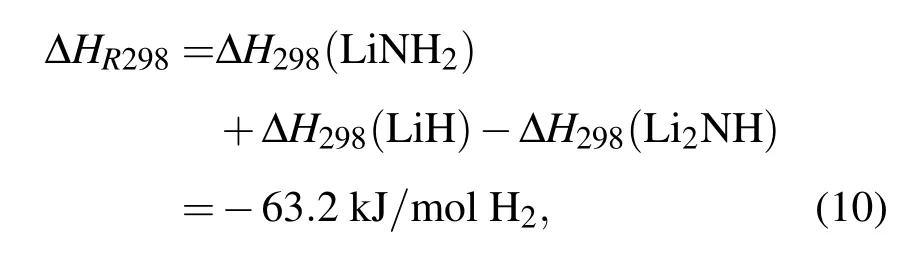
这与 Herbst和 Hector[13]的计算结果 ΔHR298=-73.6 kJ/mol符合一致,且更加接近于通过范特霍夫方程获得的反应焓实验值-66.6 kJ/mol H2[33].于大龙等[34]基于密度泛函理论的赝势-平面波方法计算得到包含零点能Li2NH+H2⇔LiNH2+LiH的可逆储氢反应的反应焓为-69.5 kJ/mol H2.

4 结论

本文采用基于密度泛函理论的平面波赝势方法计算了Li3N储氢过程中各个化合物的晶胞参数、生成焓和化学反应焓.计算得到的晶格参数与相应的实验值均符合较好.对Li3N,LiH,LiNH2和Li2NH在298 K的生成焓进行了计算,结果分别为-168.7,-81.0,-173.0和-190.8 kJ/mol,也与先前实验值和理论值符合得较好.整个储氢反应过程在T=298 K时反应焓为78.5 kJ/mol H2,这和他人计算得到T=300 K的结果75.67 kJ/mol H2[13]非常接近.同时我们给出了储氢两个过程在T=298 K时反应焓,与现有的实验和他人理论得到的数据符合较好.这些理论结果不但对储放氢有理论指导意义,而且对储氢材料的研究、开发和利用也有极重要的实际意义.

[1]Ichikawa T,Isobe S,Hanada N,Fujii H 2004J.Alloys Compd.365271

[2]Meisner G P,Pinkerton F E,Meyer M S,Balogh M P,Kundrat M D 2005 J.Alloys Compd.24 404

[3]Chen P,Xiong Z,Luo J,Lin J,Tan K L 2003 J.Phys.Chem.B 107 10967

[4]Noritake T,Nozaki H,Aoki M,Towata S,Kitahara G,Nakamori Y,Orimo S 2005 J.Alloys.Compd.393 264

[5]Ohoyama K,Nakamori Y,Orimo S,Yamada K 2005 J.Phys.Soc.Jpn.74 483

[6]Balogh M P,Jones C Y,Herbst JF,Hector Jr L G,Kundrat M 2006 J.Alloys Compd.420 326

[7]Kohn W,Sham L J1965 Phy.Rev.137 A 1697

[8]Li Q,Huang D H,Cao Q L,Wang FH 2013 Chin.Phys.B 22 037101

[9]Chen X,Chen WB,Shang X F,Tao X M,Dai JH,Tan M Q 2007 Acta.Phys.Chim.Sin.23 861(in Chinese)[陈鑫,陈文斌,尚学府,陶向明,戴建辉,谭明秋2007物理化学学报23 861]

[10]Chen ZJ,Xiao HY,Zu X T 2005 Acta Phys.Sin.54 5301(in Chinese)[陈中钧,肖海燕,祖小涛2005物理学报54 5301]

[11]The ABINIT code is a common project of the Universit´e Catholique de Louvain,and other contributors(URL http：//www.abinit.org)

[12]Troullier N,Martins JL 1991 Phys.Rev.B 43 1993

[13]Herbst JF,Hector L G 2005 Phys.Rev.B 72 125120

[14]Miwa K,Ohba N,Towata S 2006 Phys.Rev.B 74 075110

[15]Siegel Donald J,Wolverton C,Ozolinˇs V 2007 Phys.Rev.B 75 014101

[16]David R 1986 CRC Handbook of Chemistry and Physics(Vol.67)(Boca Raton：CRCPress)pF-159

[17]Villars P,Calvert L D 1991 Pearson’s Handbook of Crystallographic Data for Intermetallic Phases(2nd Ed.)(Metals Park,OH：American Society of Metals)

[18]Smith D K,Leider H R 1968 J.Appl.Crystallogr.1 246.

[19]Rabenau A,Schulz H 1976 J.Less-Common Met.50 155

[20]Jacobs Von H,Juza R 1972 Z.Anorg.Allg.Chem.391 271

[21]Nagib M,Jacobs H 1973 Atomkernenergie 21 275

[22]Magyari-K¨ope B,Ozolinˇs V,Wolverton C 2006 Phys.Rev.B 73 220101(R)

[23]Miwa K,Ohba N,Towata SI,Nakimori Y,Orimo SI 2005 Phys.Rev.B 71 195109

[24]Hino S,Ichikawa T,Ogita N,Udagawa M,Kojima Y 2009 J.Appl.Phys.105 023527

[25]Hino S,Ichikawa T,Koijma Y 2010 J.Chem.Thermodynamics42 140

[26]Barin I1995 Thermochemical Data of Pure Substances(3rd Ed.)(New York：VCH)

[27]Song Y,Guo Z X 2006 Phys.Rev.B 74 195120

[28]Ruff O,Goerges H 1910 Chem.Ber.44 502

[29]Chase Jr M W 1998NIST-JANAFThemo-chemical Tables(4th Ed.)(J.Phys.Chem.Ref.Data,Monograph,Vol.9)