一维三振子周期结构带隙设计*

高明 吴志强

1)(天津大学机械工程学院力学系,天津 300072)

2)(山东科技大学理学院力学系,青岛 266590)

(2012年12月24日收到;2013年4月1日收到修改稿)

1 引言

周期结构是由基本单元在空间周期排列形成的结构.在土木工程、机械动力、航空航天等领域中有广泛应用,如加筋梁板、蜂窝结构、栅格结构、阶梯轴等[1].声子/光子晶体也是典型的周期结构，其弹性常数/介电常数周期性变化，且具有弹性波/电磁波带隙[2],是当今物理学、光电子学、电磁场理论、材料科学、纳米技术、微机电等领域共同关注的研究热点.

周期结构具有特殊的色散关系,色散关系曲线之间的频率范围称为带隙,带隙频率范围内的弹性波传播受到抑制,而其他频率范围(通带)内的弹性波可以无损耗地传播[3].因此,周期结构可作为减振单元用于振动控制[4-7].由于是宽频带的振动控制方法,对激励频率的波动不敏感,既适合于激励源的频率不稳定的振动控制,也适用于共振频率密集结构的振动控制.

计算带隙是周期结构研究的重要问题,已发展的计算方法主要包括传递矩阵法[8]、平面波展开法[9]、时域有限差分法[10]、多重散射法[11]、集中质量法[12,13]等.其中集中质量法有精度高、收敛性好等优点,特别适合一维周期结构的带隙计算.利用集中质量法可将一维周期结构等效为周期弹簧振子系统[12-14],振子的质量和弹簧的刚度由一维周期结构中的等效弹性模量、长度、截面尺寸等参数得到.已有研究表明,既可以适当选择周期结构中单元的材料和几何参数,调节周期结构带隙范围[3,5],也可利用智能材料(如压电晶体[4,15-17]、形状记忆合金[18,19]、功能梯度材料[20,21]等)主动改变弹性模量,调节带隙范围.

目前有关带隙的研究,大部分从正问题的角度进行讨论,而对如何设计周期结构实现特定频率范围的带隙这一反问题,还极少涉及.因此,发展周期结构带隙设计方法有重要的理论意义和潜在的工程应用价值.

作为带隙设计的初步探讨,本文针对一维三振子周期结构,引入奇异性理论分析其色散曲线拓扑结构,给出带隙起止频率的计算公式,进而提出此类结构带隙设计方法并进行验证.

2 带隙计算

图1所示为一个无限周期弹簧振子结构.每个周期由3个弹簧及振子串联而成,相应的弹簧刚度系数为k1,k2,k3,相应的振子质量为m1,m2,m3,相邻振子间距均为d,每个周期的长度为a=3d.如图1,假定弹簧的质量全部集中在振子上,且振子只能在图示的水平方向即x方向运动,xj为对应振子mj的位移.对于第 j个振子,其运动方程为

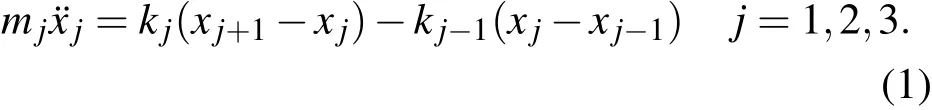
根据Bloch定理[22],在周期边界条件下,上述运动方程的解可写为振幅为A,角频率为ω的简谐振动：

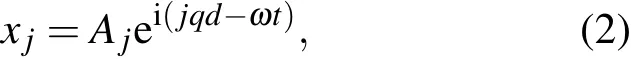
式中 jq表示第 j个振子的位相因子,q为波矢,在第一Brillouin区即(-π/a,π/a)取值.

图1 一维三振子周期结构

将(2)式代入((1)式,得：)

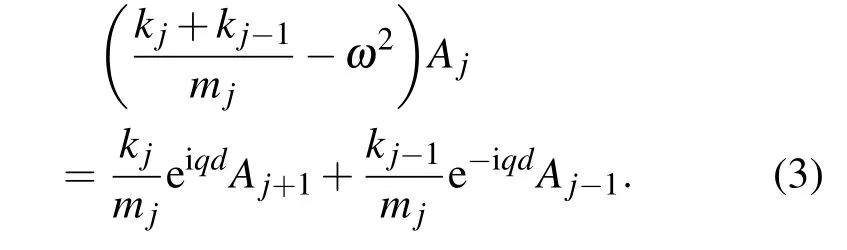
由于弹簧振子结构周期排列,在周期边界条件下有：

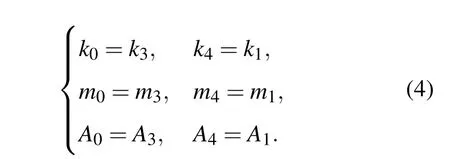
方程(3)可简化为

要使系统中存在形如(2)式的振动形式,则(5)式系数行列式必须等于零,即

将特定的m1,m2,m3和k1,k2,k3代入(6)式,且令qd∈(-π/3,π/3)便可得到三条色散曲线.图2所示为m1=1 kg,m2=0.2 kg,m3=0.77 kg,k1=k2=k3=800 N/m的色散曲线.色散曲线上的每个点都对应于周期结构中的一种弹性波的传播模式.所有色散关系曲线都不经过的频率范围形成带隙,如图2阴影部分所示.显然,带隙上下限值与色散曲线拓扑结构有关.(6)式中参数变化时,会不会导致色散曲线拓扑结构变化还没有明确结论,为此下节引入分岔分析的奇异性理论进行讨论.

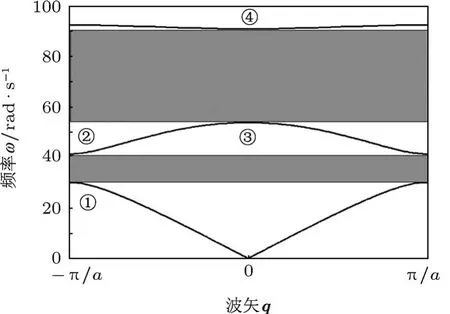
图2 一维三振子周期结构色散曲线

3 奇异性分析及带隙起止频率

由于方程(6)中有6个参数m1,m2,m3和k1,k2,k3,数目较多,不便于进行分析,下面对其进行无量纲化处理.令：

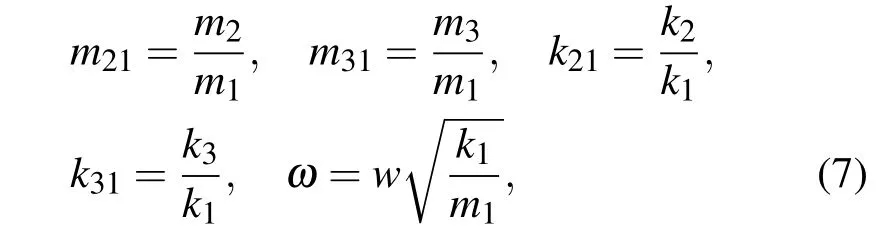
则方程(6)可简化为无量纲方程：该方程描述了无量纲参数与无量纲频率间的关系.当m21=m31=k21=k31=1时,带隙不存在,本文不考虑这种特殊情况.

若视q为分岔参数,w为状态变量,则根据奇异性理论[23],方程(8)对应的色散曲线存在不同形式的拓扑结构时,参数空间中必然存在非空的临界参数集合,即转迁集.转迁集将参数空间分成不同区域,不同区域中的分岔曲线的拓扑结构一般是不同的.相反,如果所有转迁集都为空集,则色散曲线的拓扑结构不随参数的变化而变化,也就说完全可按图2的特点来确定带隙的位置.

若记w0=w2,gw0,gw0w0和gq分别为g关于w0的一阶、二阶导数和关于q的一阶导数.则转迁集包括分岔集B,滞后集H和双极限点集DL,分别为

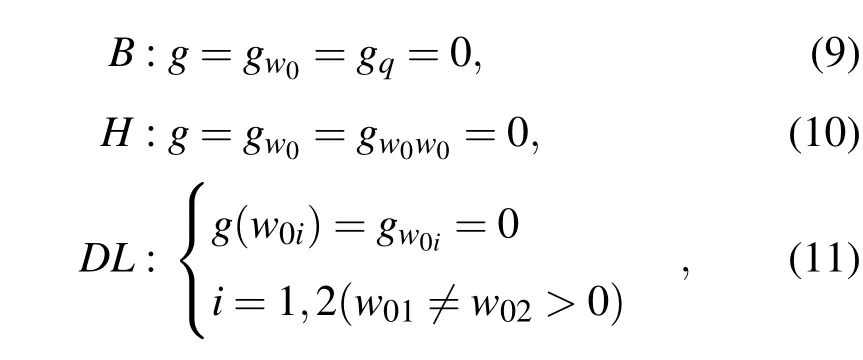
g,gw0和gw0w0的表达式见附录.

先计算分岔集B：

若视(12)式为关于m21的一元二次方程，则由于判别式可知(12)式没有m21实数根,也就是说没有任何参数组合满足分岔集B的条件,集合B为空集.

再看滞后集H：

由gw0=gw0w0=0联立消去的w0,可得参数需满足的方程为

同样，由于其判别式

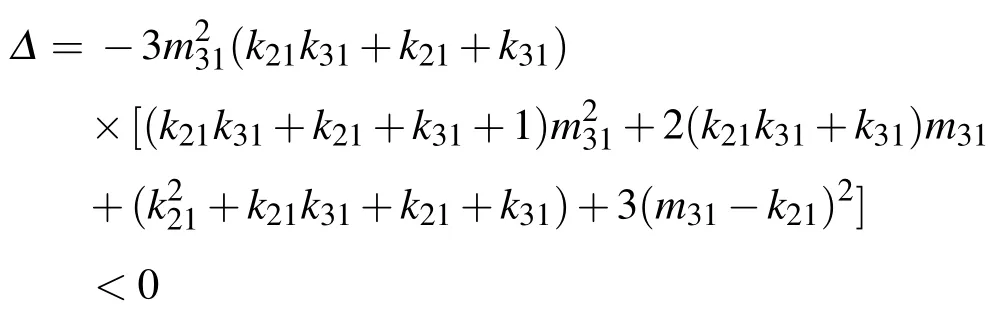
可知方程(13)无解,因此集合H也为空集.

对于双极限点集DL而言,因g关于w0最高次次数为3,也为空集.

B,H和DL均为空集,表明不管周期结构的质量参数和刚度参数如何变化,色散曲线均保持图2所示的结构.又由(8)式可知色散曲线极值点位置也只与qd有关,而与其他参数无关.因此第一带隙的上下限恒为图2①,②点的频率值,第二带隙的上下限恒为图2③,④点的频率值.

由一元三次代数方程的求根公式，可得第一带隙的起始频率、截止频率为

第二带隙的起始频率、截止频率为

其中,

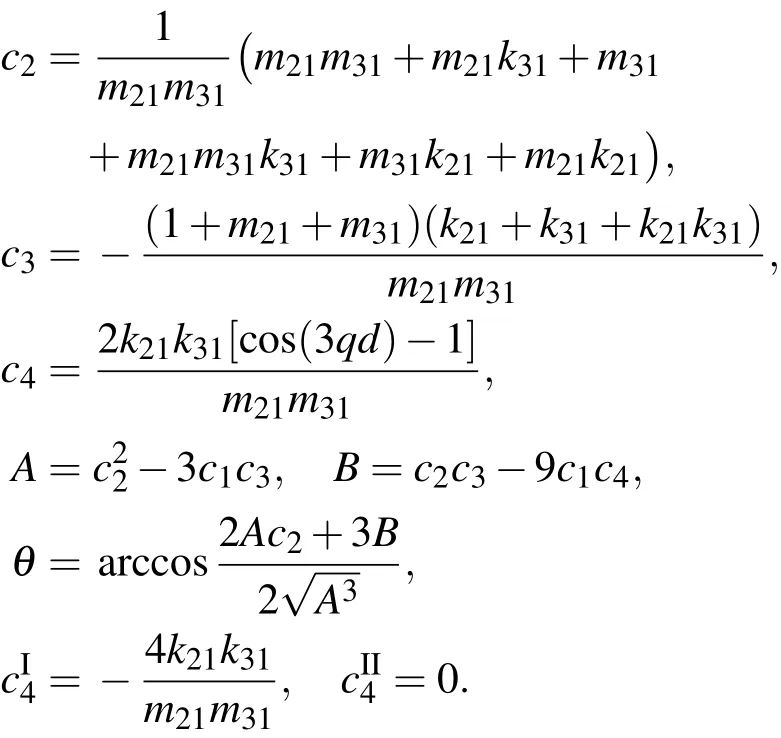
4 带隙设计方法及举例

由于在振动带隙内,结构没有对应的振动模式,即当外激励频率在带隙范围内时,振动在结构中的传播大大减弱.带隙设计的任务就是根据外激励频率的范围,选取合适振子的质量和弹簧刚度,使外激励频率落在带隙范围内,从而起到隔振减振的效果.

4.1 带隙设计方法

根据以上奇异性分析结果,振动带隙的起止频率只与三条色散曲线的边值点有关.控制带隙范围主要控制色散曲线的边值点(图2中的①—④点)的数值即可.因此,带隙设计可按以下步骤进行：

1)将所需设计的第一、二带隙的无量纲边值条件wI1,wI2,wII1,wII2依次代入无量纲色散方程中,得到含有m21,m31,k21和k31的关系式;

2)找到满足带隙设计要求的m21,m31,k21和k31取值范围;

3)在各参数的取值范围内,选取合理数值,根据实际工程情况,选取实际参数完成带隙设计.

为简便起见,下面针对等刚度和等质量两种情况分别进行带隙设计.

4.2 等刚度系统带隙设计

对于等刚度系统,k21=k31=1,(8)式简化为

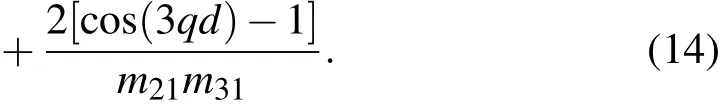
假如设计第一带隙角频率为11.5—18 rad/s,第二带隙角频率为25—40 rad/s,即图2中①—④各极值点的数值分别为

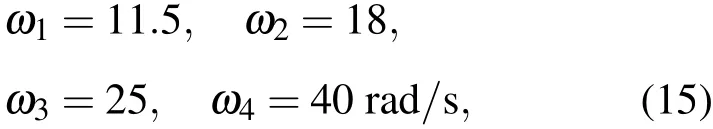
则可取对应无量纲频率带隙边值条件w1=wI1=1.15,w2=wI2=1.8,w3=wII1=2.5,w4=wII2=4,在方程(14)关于w的解中分别找到与四个边值条件对应的三条色散曲线上①—④的数值,得到质量比m21,m31需满足的条件,画出m21,m31的关系曲线,如图3中①—④所示.

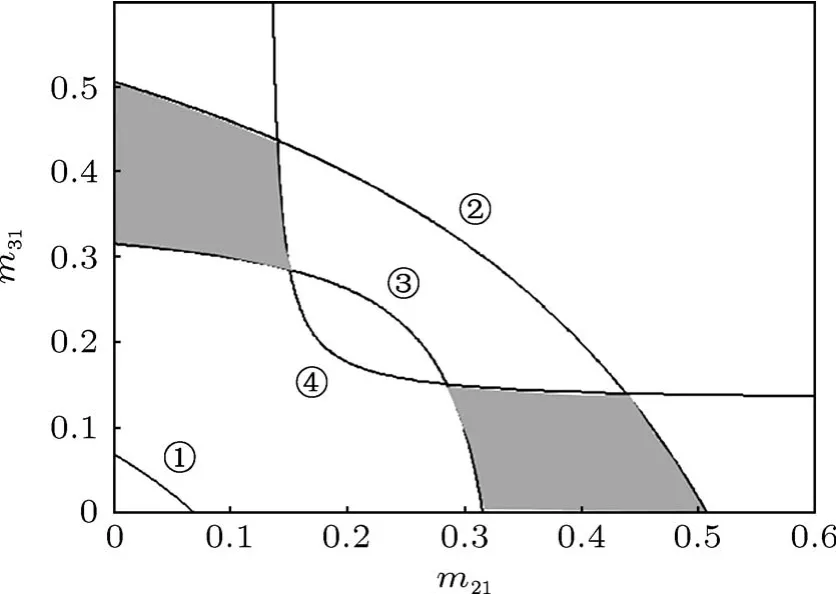
图3 等刚度系统振子质量比设计区域

实际带隙的宽度不小于设计带隙即满足设计要求.具体来说,①点数值小于1.15,②点的数值大于1.8,③点数值小于2.5,④点数值大于4.易于验证在图3中阴影区选择m21和m31时,上述要求即可满足.以下通过例子验证这一结论是正确的.

今选取阴影区域中的一点m21=0.14,m31=0.43.再根据(15)式的设计要求,可以把频率的数值取为10,实际参数选取如下：

将(16)式各值代入(6)式,画出色散曲线如图4(a)所示.从图中可以看出,①—④点全部满足(15)式的设计要求.为验证带隙设计结果的正确性,画出10个周期三振子系统振动传输特性曲线,如图4(b)所示,可以看出在振幅较大衰减的区域恰好与带隙位置相对应.说明在等刚度情况下,本文提出的设计方法是有效的.

图4 等刚度系统色散曲线与传输特性曲线图

4.3 等质量系统带隙设计

对于等质量系统m21=m31=1,(8)式简化为

假设还按(15)式的带隙设计要求,取对应无量纲频率带隙边值条件w1=wI1=1.15,w2=wI2=1.8,w3=wII1=2.5,w4=wII2=4,由方程(17)可得到质量比k21,k31所需满足的条件,画出k21,k31的关系曲线,如图5中①—④所示.在图5阴影区域选择满足带隙设计要求的一点k21=10,m31=2.5.仍然可以把频率的数值取为10,实际参数选取如下：

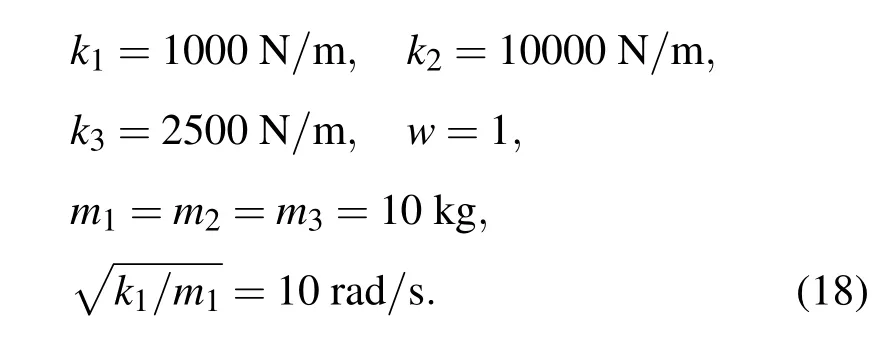
将(18)式各值代入(6)式,画出色散曲线如图6(a)所示.图6(b)为10个周期三振子系统的振动传输特性曲线.从图中可以看出,①—④点亦全部满足(15)式的设计要求.因此在等质量情况下,本文提出的设计方法也是有效的.对不等刚度和不等质量的情况,由于受篇幅限制,此处不再举例.

利用集中质量法中振子质量和弹簧刚度与连续介质材料参数之间的关系,可将周期弹簧振子结构带隙设计方法应用到一维杆状周期结构带隙设计中,还可以对含有智能材料主动构件的周期结构进行带隙设计.也可应用于声子晶体的带隙设计,不仅有助于推动声子晶体在减振降噪中早日得到广泛应用,还将为光子晶体的带隙设计提供参考.

图5 等质量系统弹簧刚度设计区域

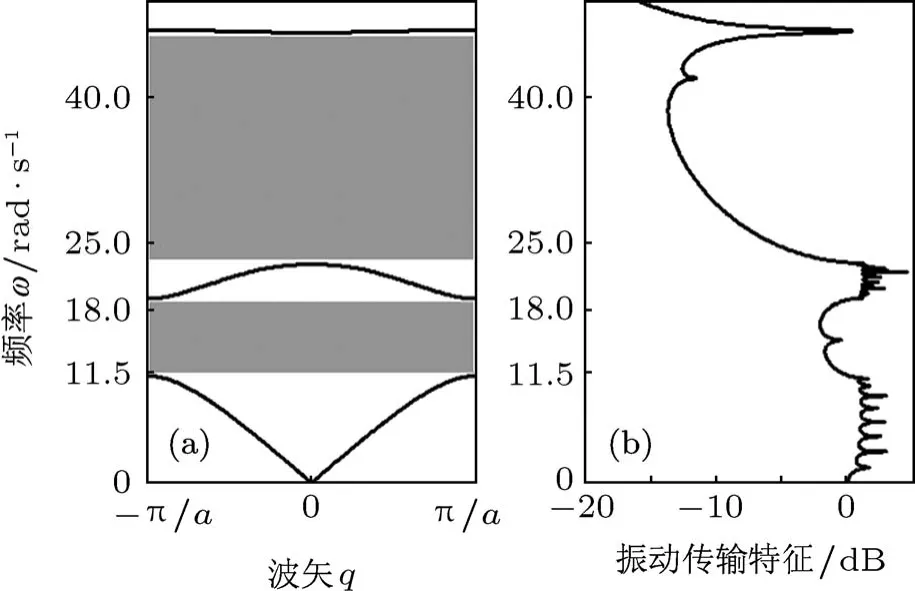
图6 等质量系统色散曲线与传输特性曲线图

5 结论

针对一维三振子周期结构,对其色散方程进行奇异性分析,表明色散曲线的拓扑结构不随质量和刚度等参数的变化而变化,进而确定带隙范围,给出两个带隙起止频率公式.作为带隙设计实例,分别对等刚度和等质量系统两种情况进行了讨论,给出了具体设计过程,通过具体算例进行了验证.设计结果能够达到预期目的.这为在减振降噪等领域设计周期结构提供了一定的理论依据和参考.

附录 g,gw0和gw0w0的表达式

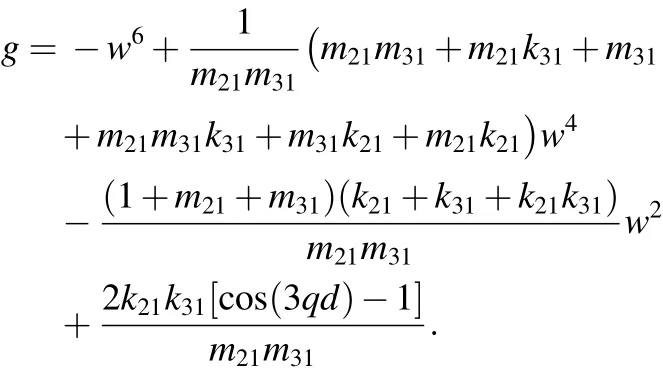
[1]Chen B,Huang X C 2011 Noise and Vibration Control 31 37(in Chinese)[陈斌,黄修长2011噪声与振动控制31 37]

[2]Wen X S2006 Theoryand Technologyof Photonic and Phononic Crystals(Beijing：Science Press)p4(in Chinese)[温熙森 2006 光子/声子晶体理论与技术(北京：科学出版社)第4页]

[3]Wen JH 2005 Ph.D.Dissertation(Changsha：National University of Defense Technology)(in Chinese)[温激鸿2005博士学位论文(长沙：国防科技大学)]

[4]Asiri S,Baz A,Pines D 2006 Smart Mater.Struct.15 1707

[5]Richards D,Pines D J2003 J.Sound Vib.264 317

[6]Huang X C,Feng G P,Zhang Z Y,Hua H X 2010 Noise and Vibration Control 30 9(in Chinese)[黄修长,冯国平,张志谊,华宏星2010噪声与振动控制30 9]

[7]Cheng S X 2012 M.S.Dissertation(Shanghai：Shanghai Jiao Tong University)(in Chinese)[程世祥2012硕士学位论文(上海：上海交通大学)]

[8]Shen H J,Wen JH,Yu D L,Wen X S 2009 Acta Phys.Sin.58 8357(in Chinese)[沈惠杰,温激鸿,郁殿龙,温熙森2009物理学报58 8357]

[9]Cao Y J,Yun GH,Na RS2011 Acta Phys.Sin.60 077502(in Chinese)[曹永军,云国宏,那日苏2011物理学报60 077502]

[10]Kafesaki M,Sigalas M M,Garcia N 2000 Phys.Rev.Lett.85 4044

[11]Psarobas IE,Stefanou N,Modinos A 2000 Phys.Rev.B 62 278

[12]Wang G,Wen JH,Liu Y Z 2004 Phys.Rev.B 69 184302

[13]Wen JH,Wang G,Liu Y Z,Yu D L 2004 Acta Phys.Sin.53 3384(in Chinese)[温激鸿,王刚,刘耀宗,郁殿龙2004物理学报53 3384]

[14]Baz A 2001 J.Vib.Acoust.123 472

[15]Singh A,Pines D J,Baz A 2004 Smart Mater.Struct.13 698

[16]Wang G,Chen SB,Wen JH 2010 Smart Mater.Struct.20 015026

[17]Thorp O,Ruzzene M,Baz A 2001 Smart Mater.Struct.10 979

[18]Ruzzene M,Baz A 2000 Smart Mater.Struct.9 805

[19]Yeh JY,Chen L W 2006 Compos.Struct.73 53

[20]Su X L,Gao Y W 2010 J.Functional Mater.41 368(in Chinese)[宿星亮,高原文2010功能材料41 368]

[21]Wu M L,Wu L Y,Yang WP 2009 Smart Mater.Struct.18 115013

[22]Huang K 1988 Solid State Physics(Beijing：Higher Education Press)p154(in Chinese)[黄昆1988固体物理学(北京：高等教育出版社)第154页]

[23]Golubitsky M,Schaeffer D G 1985 Singularitiesand Groupsin Bifurcation Theory(Vol.1)p140(New York：Springer-Verlag)